前言

Hello！小伙伴！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖…已保研。目前正在学习C++/Linux/Python
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
机器学习小白阶段
文章仅作为自己的学习笔记 用于知识体系建立以及复习
知其然 知其所以然！

系列文章

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（1）：图的基本概念

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（2）：图的矩阵表示

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（3）：路径与连通

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（4）：有向图的连通性

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（5）：树及其性质

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（6）：生成树算法

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（7）：连通度

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（8）：割边、割集、割点

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（9）：匹配的概念

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（10）：匹配基本定理

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（11）：欧拉图

6.3 有向欧拉图

定于 6.2

设$G=(V,E)$是弱连通有向图

有向巡回

经过$G$的每条弧至少一次的有向闭通路成称为有向巡回

有向欧拉巡回

经过$G$的每条弧正好一次的有向巡回称为有向欧拉巡回

有向欧拉图

存在有向欧拉巡回的有向图称为有向欧拉图

有向欧拉道路

经过$G$的每条弧正好一次的有向道路称为有向欧拉道路

定理 6.4

$G$是弱连通有向图，则下述命题等价

1. $G$是有向欧拉图
2. $\forall v\in V(G),d^{-}(v)=d^{+}(v)$
3. $G={\bigcup }_{i=1}^n{C}_i$，其中$C_i$是有向圈，且$E(C_i)\cap E(C_j)=\varphi ,i\le i<j\le n$，$n$为某个自然数

推论 6.4

有向圈$G$有以$u_1$为起点，以$u_2$为终点的有向欧拉道路的充要条件是：$G$是弱连通有向图，且满足

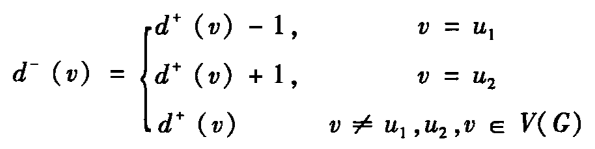
结语

说明：

• 参考于 课本《图论》
• 配合书中概念讲解 结合了自己的一些理解及思考

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正

文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/121545744