【数据结构与算法】之判断一个整数是否是 4 的幂次方的高逼格算法

一、题目要求

• 给定一个整数 (32 位有符号整数)，请编写一个函数来判断它是否是 4 的幂次方。
• 示例一：

	输入: 16
	输出: true

  

 

  
1
  
2
 

• 示例二：

	输入: 5
	输出: false

  

 

  
1
  
2
 

• 进阶：
  你能不使用循环或者递归来完成本题算法吗？

二、算法示例

• 这道题最直接的方法就是 快速查找方法缓存 不停的去除以 4 ，看最终 快速查找方法缓存 结果是否为 1 ，参见算法如下：

	class Solution {
	    public boolean isPowerOfFour(int num) {
	         while ( (num != 0)  && (num % 4 == 0)) {
	            num /= 4;
	        }
	        return num == 1;
	    }
	}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

• 不过这个算法使用了循环 ，逼格不够高。我们都知道： 对于一个整数而言，如果这个数是 4 的幂次方，那它必定也是 2 的幂次方 。
• 那么先将 2 的幂次方列出来，来找一下其中哪些数是 4 的幂次方：

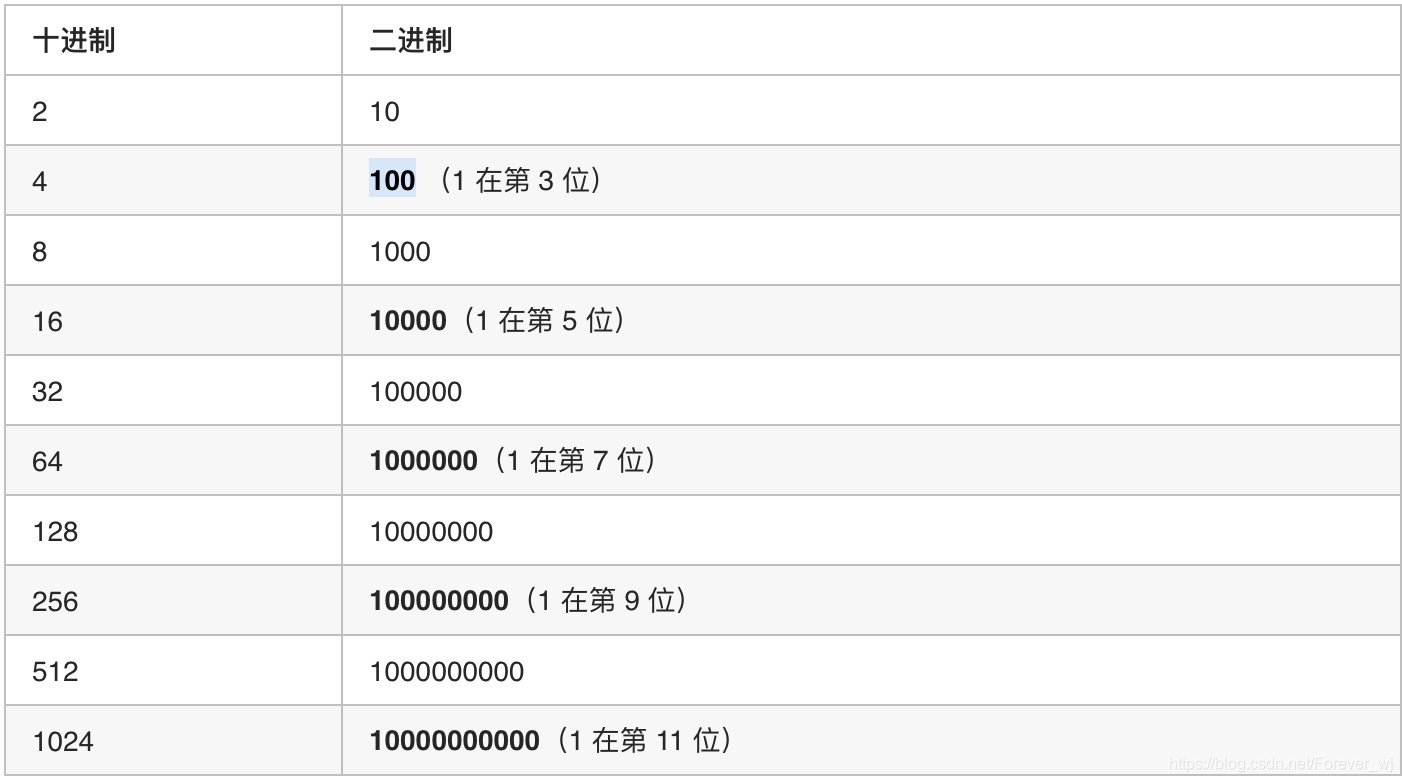
• 不难发现： 4 的幂次方的数的二进制表示 1 的位置都是在奇数位 。
• 其实， 判断一个整数是否是 2 的幂次方数，使用的是位运算 n & ( n - 1 ) 。同样的，这里就可以使用位运算：将这个数与特殊的数做位运算。
• 这个特殊的数有如下特点：
  • 足够大 ，但 不能超过 32 位 ，即最大为 1111111111111111111111111111111（ 31 个 1）；
  • 它的二进制表示中 奇数位为 1 ， 偶数位为 0 ；
• 那么符合这两个条件的二进制数是：

	1010101010101010101010101010101

  

 

  
1
 

• 如果用一个 4 的幂次方数和它做与运算，那么得到的还是 4 的幂次方数 。原理如下：

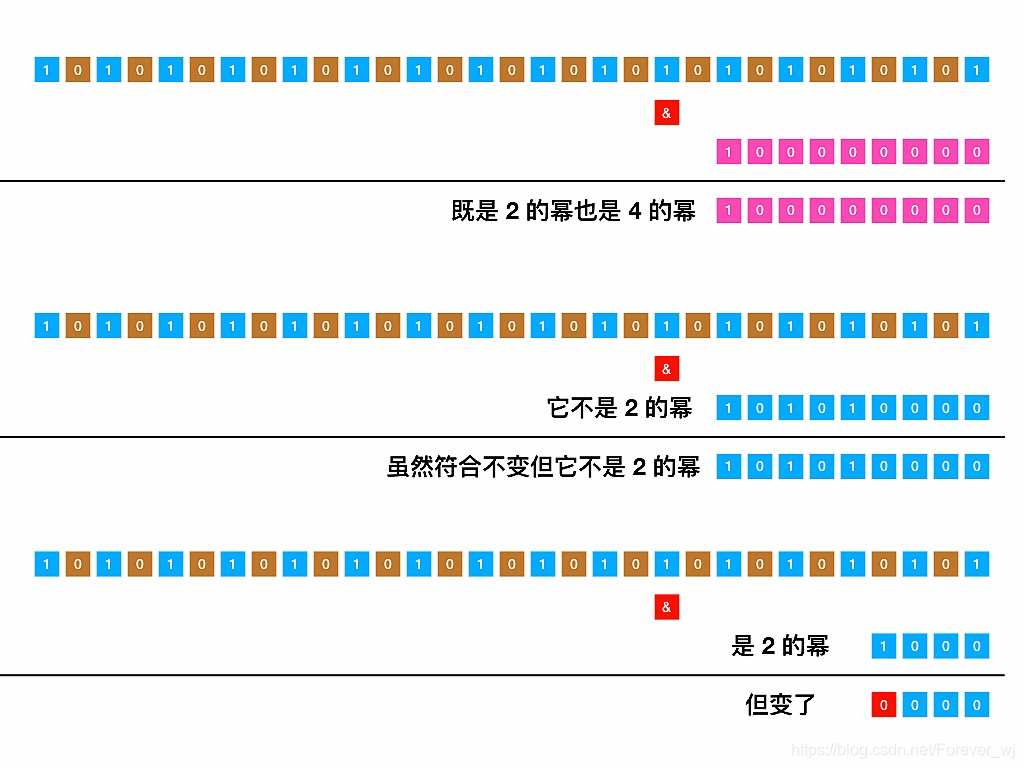
• 将这个二进制数转换成 16 进制表示： 0x55555555 ，如下图所示，有没有感觉逼格更高了？

• 算法示例如下：

	class Solution {
	    public boolean isPowerOfFour(int num) {
	        if (num <= 0)
				return false;
	        // 先判断是否是 2 的幂
			if ((num & num - 1) != 0)
				return false;
	        // 如果与运算之后是本身则是 4 的幂
			if ((num & 0x55555555) == num)
				return true;
			return false;
	    }
	}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

文章来源: blog.csdn.net，作者：Serendipity·y，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Forever_wj/article/details/108786082