【数据结构与算法】之N个数中有K个数可能的组合算法

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

一、题目要求

	输入: n = 4, k = 2
	输出:
	[
	  [2,4],
	  [3,4],
	  [2,3],
	  [1,2],
	  [1,3],
	  [1,4],
	]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

二、示例算法

① Swift

• 因结果集合全是由小到达排序的方式，所以不用考虑去重复，因此流程变得简单多了；
• 用一个数组t来记录目前已经访问数据、如果数组中的元素数量等于 k 意味着找到了一组答案，存到 res 中；
• 每次递时记录数据时起始元素为 t 数组中最后一个+1，并判断剩余未遍历的数据的数据是否还够用；
• 如果不够用了，直接没有必要继续向下遍历直接返回。

	var res = [[Int]]()
    func bt(_ n:Int, _ count:Int, _ t:[Int]){
        let tLen = t.count
        if tLen == count {
            res.append(t);
            return;
        }
        
        let minT = t.count > 0 ? t.last!+1 : 1
        if minT > n || n-minT+1 < count-tLen {
        	return;
        }
        var tmp = t
        
        for i in minT ... n {
            tmp.append(i)
            bt(n,count,tmp)
            tmp.removeLast()
        }
    }
    
    func combine(_ n: Int, _ k: Int) -> [[Int]] {
        let tmp = [Int]()
        bt(n, k, tmp)
        return res
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
 

② Java

• Java实现：既然是树形问题上的深度优先遍历，因此首先画出树形结构。例如输入：n = 4, k = 2，我们可以发现如下递归结构：
  • 如果组合里有 1 ，那么需要在 [2, 3, 4] 里再找 1 个数；
  • 如果组合里有 2 ，那么需要在 [3, 4] 里再找 1 个数。
  • 注意：这里不能再考虑 1，因为包含 1 的组合，在第 1 种情况中已经包含。
  • 依次类推（后面部分省略），以上描述体现的 递归 结构是：在以 n 结尾的候选数组里，选出若干个元素。画出递归结构如下图：

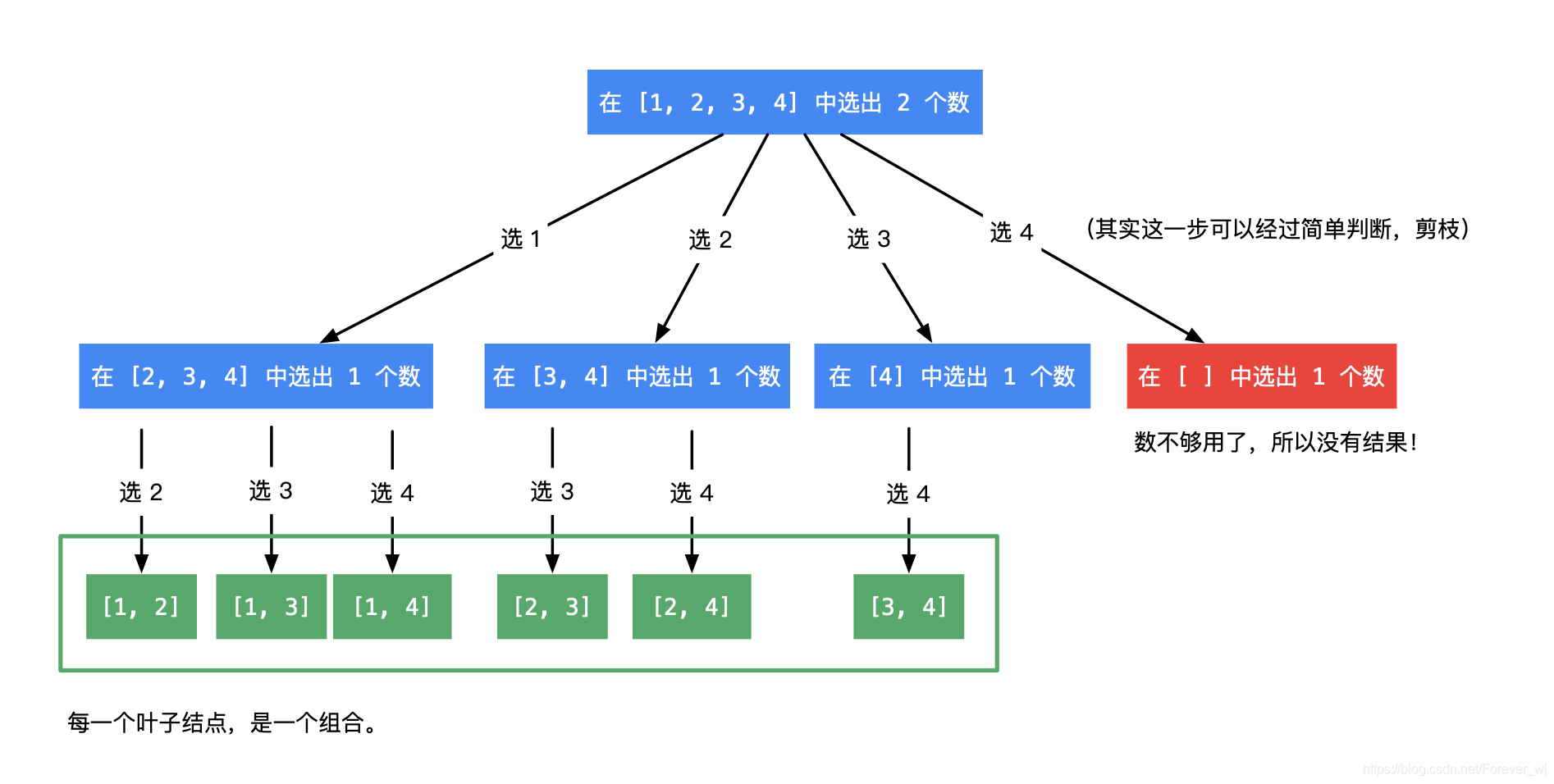
• 说明：
  • 叶子结点的信息体现在从根结点到叶子结点的路径上，因此需要一个表示路径的变量 path，它是一个列表，特别地，path 是一个栈；
  • 每一个结点递归地在做同样的事情，区别在于搜索起点，因此需要一个变量 start ，表示在区间 [begin, n] 里选出若干个数的组合。
• Java 算法一：

	public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        // 从 1 开始是题目的设定
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 遍历可能的搜索起点
        for (int i = begin; i <= n; i++) {
            // 向路径变量里添加一个数
            path.addLast(i);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
            dfs(n, k, i + 1, path, res);
            // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
            path.removeLast();
        }
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
 

• Java 算法二：

	public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i <= n; i++) {
            path.addLast(i);
            System.out.println("递归之前 => " + path);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
            System.out.println("递归之后 => " + path);
        }
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int n = 5;
        int k = 3;
        List<List<Integer>> res = solution.combine(n, k);
        System.out.println(res);
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
 

• 优化：分析搜索起点的上界进行剪枝
• 上面的代码，搜索起点遍历到 n，即：递归函数中有下面的代码片段：

	// 从当前搜索起点 begin 遍历到 n
	for (int i = begin; i <= n; i++) {
	    path.addLast(i);
	    dfs(n, k, i + 1, path, res);
	    path.removeLast();
	}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

• 事实上，如果 n = 7，k = 4，从 5 开始搜索就已经没有意义了，这是因为：即使把 5 选上，后面的数只有 6 和 7，一共就 3 个候选数，凑不出 4 个数的组合。因此，搜索起点有上界，这个上界是多少，可以举几个例子分析。
• 分析搜索起点的上界，其实是在深度优先遍历的过程中剪枝，剪枝可以避免不必要的遍历，剪枝剪得好，可以大幅度节约算法的执行时间。
• 下面的图片绿色部分是剪掉的枝叶，当 n 很大的时候，能少遍历很多结点，节约了时间。

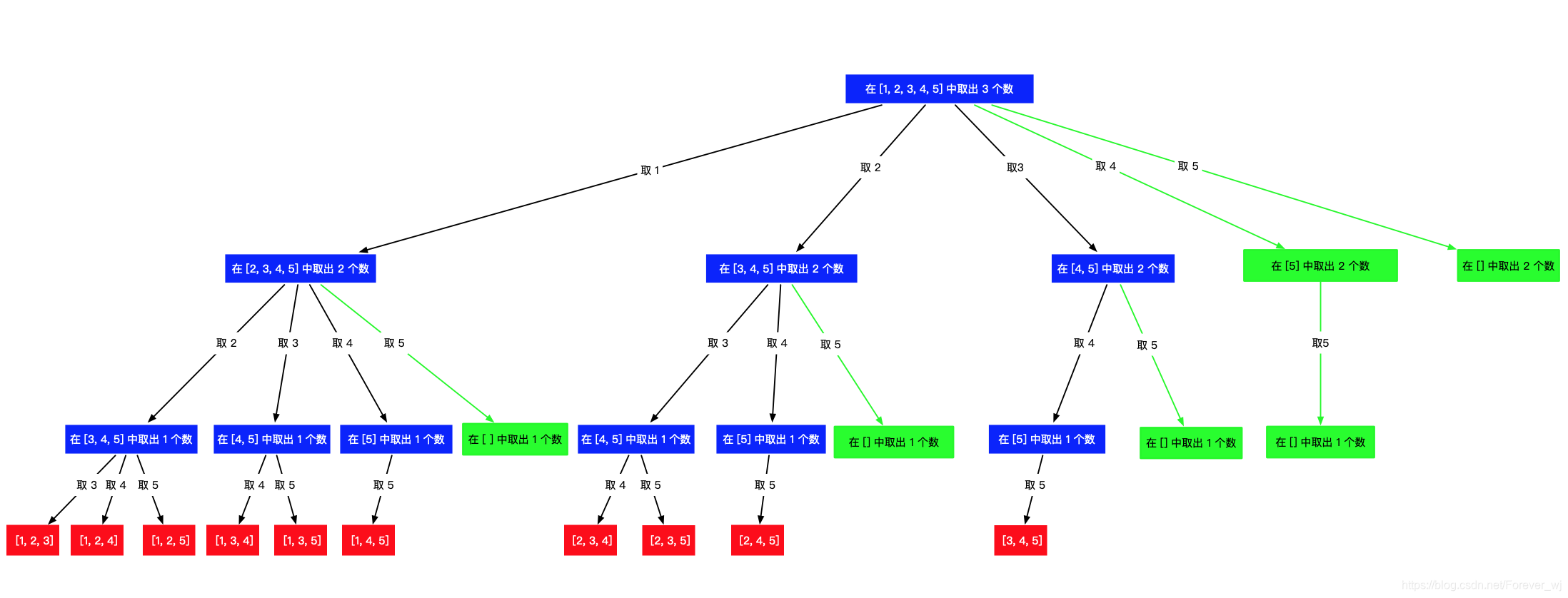
• 容易知道：搜索起点和当前还需要选几个数有关，而当前还需要选几个数与已经选了几个数有关，即与 path 的长度相关。举几个例子分析：
• 例如：n = 6 ，k = 4：
  • path.size() == 1 的时候，接下来要选择 3 个数，搜索起点最大是 4，最后一个被选的组合是 [4, 5, 6]；
  • path.size() == 2 的时候，接下来要选择 2 个数，搜索起点最大是 5，最后一个被选的组合是 [5, 6]；
  • path.size() == 3 的时候，接下来要选择 1 个数，搜索起点最大是 6，最后一个被选的组合是 [6]；
• 再如：n = 15 ，k = 4：
  • path.size() == 1 的时候，接下来要选择 3 个数，搜索起点最大是 13，最后一个被选的是 [13, 14, 15]；
  • path.size() == 2 的时候，接下来要选择 2 个数，搜索起点最大是 14，最后一个被选的是 [14, 15]；
  • path.size() == 3 的时候，接下来要选择 1 个数，搜索起点最大是 15，最后一个被选的是 [15]；
• 结论：搜索起点的上界 + 接下来要选择的元素个数 - 1 = n。
• 接下来要选择的元素个数 = k - path.size()，整理得到：

	搜索起点的上界 = n - (k - path.size()) + 1

  

 

  
1
 

• 因此我们的剪枝过程就是：把 i <= n 改成 i <= n - (k - path.size()) + 1 ：

	public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int index, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 只有这里 i <= n - (k - path.size()) + 1 与参考代码 1 不同
        for (int i = index; i <= n - (k - path.size()) + 1; i++) {
            path.addLast(i);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
        }
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
 

文章来源: blog.csdn.net，作者：Serendipity·y，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Forever_wj/article/details/108633586