【数据结构与算法】之深入解析“扰乱字符串”的求解思路与算法示例
【摘要】
一、题目要求
使用下面描述的算法可以扰乱字符串 s 得到字符串 t:
如果字符串的长度为 1 ,算法停止;
如果字符串的长度 > 1 ,执行下述步骤:
在一个随机...
一、题目要求
- 使用下面描述的算法可以扰乱字符串 s 得到字符串 t:
-
- 如果字符串的长度为 1 ,算法停止;
-
- 如果字符串的长度 > 1 ,执行下述步骤:
-
-
- 在一个随机下标处将字符串分割成两个非空的子字符串。即如果已知字符串 s ,则可以将其分成两个子字符串 x 和 y ,且满足 s = x + y;
-
-
-
- 随机决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即在执行这一步骤之后,s 可能是 s = x + y 或者 s = y + x;
-
-
-
- 在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法。
-
- 给你两个长度相等的字符串 s1 和 s2,判断 s2 是否是 s1 的扰乱字符串。如果是,返回 true ;否则,返回 false 。
- 示例 1:
输入:s1 = "great", s2 = "rgeat"
输出:true
解释:s1 上可能发生的一种情形是:
"great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串
"gr/eat" --> "gr/eat" // 随机决定:「保持这两个子字符串的顺序不变」
"gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割
"g/r / e/at" --> "r/g / e/at" // 随机决定:第一组「交换两个子字符串」,第二组「保持这两个子字符串的顺序不变」
"r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法,将 "at" 分割得到 "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定:「保持这两个子字符串的顺序不变」
算法终止,结果字符串和 s2 相同,都是 "rgeat"
这是一种能够扰乱 s1 得到 s2 的情形,可以认为 s2 是 s1 的扰乱字符串,返回 true
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 示例 2:
输入:s1 = "abcde", s2 = "caebd"
输出:false
- 1
- 2
- 示例 3:
输入:s1 = "a", s2 = "a"
输出:true
- 1
- 2
- 提示:
-
- s1.length == s2.length;
-
- 1 <= s1.length <= 30;
-
- s1 和 s2 由小写英文字母组成。
二、求解算法
① 动态规划
- 给定两个字符串 T 和 S,假设 T 是由 S 变换而来:
-
- 如果 T 和 S 长度不一样,必定不能变来;
-
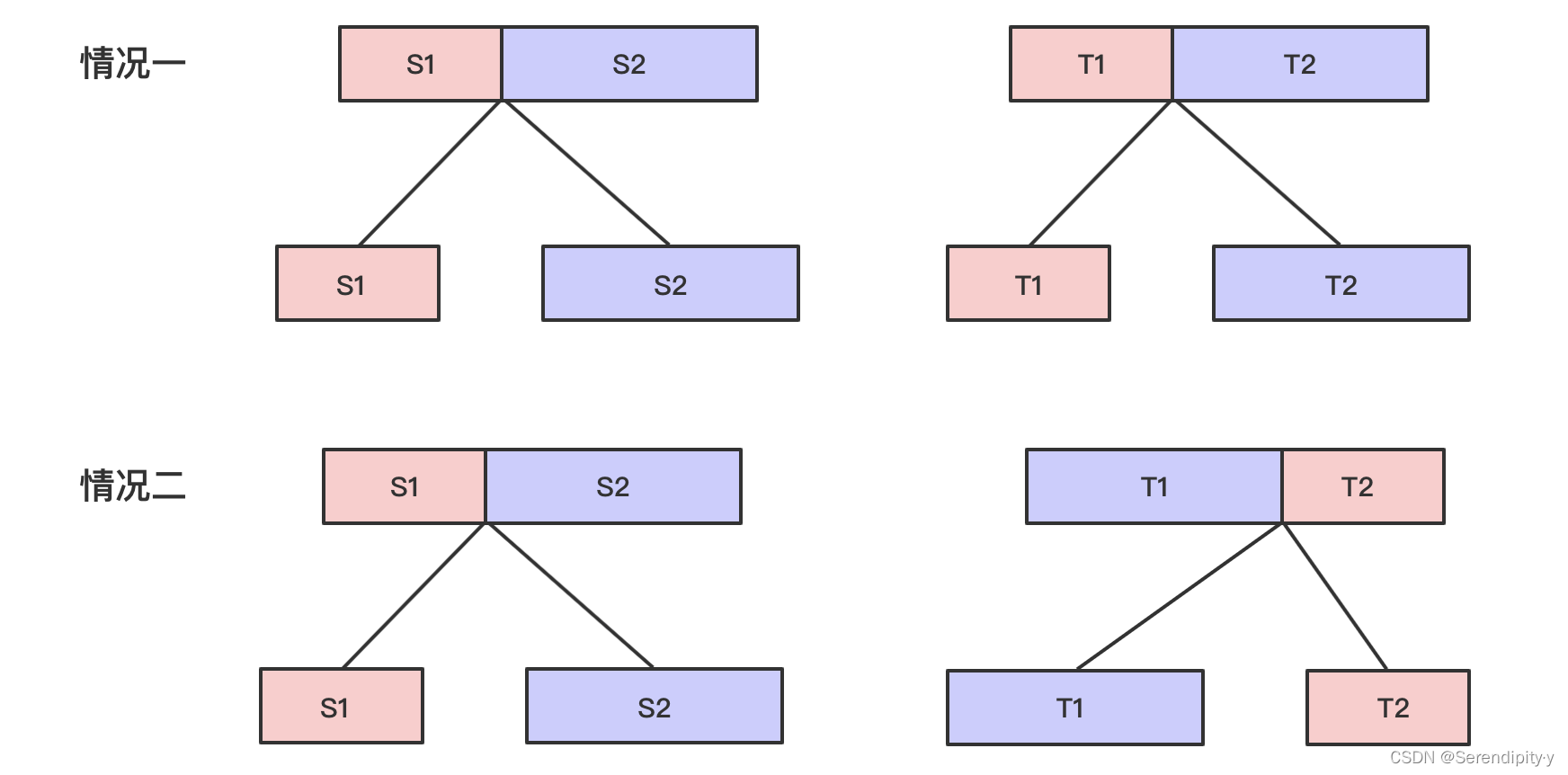
- 如果长度一样,顶层字符串 S 能够划分为 S1 和 S2,同样字符串 T 也能够划分为 T1 和 T2;
-
-
- 情况一:没交换,S1 ==> T1,S2 ==> T2;
-
-
-
- 情况二:交换了,S1 ==> T2,S2 ==> T1;
-
- 子问题就是分别讨论两种情况,T1 是否由 S1 变来,T2 是否由 S2 变来,或 T1 是否由 S2 变来,T2 是否由 S1 变来。
- dp[i][j][k][h] 表示 T[k…h] 是否由 S[i…j] 变来。由于变换必须长度是一样的,因此这边有个关系 j−i=h−k ,可以把四维数组降成三维。dp[i][j][len] 表示从字符串 S 中 i 开始长度为 len 的字符串是否能变换为从字符串T 中 j 开始长度为 len 的字符串。
- 转移方程:
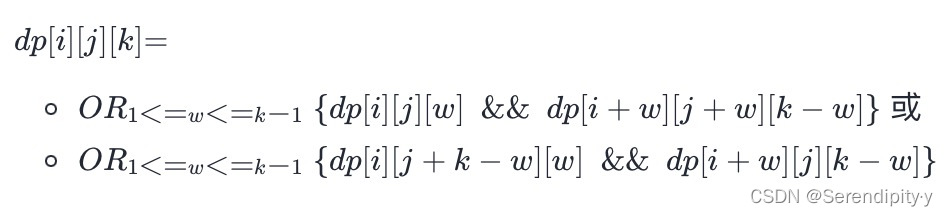
- 枚举 S1 长度 w(从 1~k−1,因为要划分),f[i][j][w] 表示 S1 能变成 T1 ,f[i+w][j+w][k−w] 表示 S2 能变成 T2 ,或者是 S1 能变成 T2 ,S2 能变成 T1。
- 初始条件:对于长度是 1 的子串,只有相等才能变过去,相等为 true,不相等为 false。
- Java 示例:
class Solution {
public boolean isScramble(String s1, String s2) {
char[] chs1 = s1.toCharArray();
char[] chs2 = s2.toCharArray();
int n = s1.length();
int m = s2.length();
if (n != m) {
return false;
}
boolean[][][] dp = new boolean[n][n][n + 1];
// 初始化单个字符的情况
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j][1] = chs1[i] == chs2[j];
}
}
// 枚举区间长度 2~n
for (int len = 2; len <= n; len++) {
// 枚举 S 中的起点位置
for (int i = 0; i <= n - len; i++) {
// 枚举 T 中的起点位置
for (int j = 0; j <= n - len; j++) {
// 枚举划分位置
for (int k = 1; k <= len - 1; k++) {
// 第一种情况:S1 -> T1, S2 -> T2
if (dp[i][j][k] && dp[i + k][j + k][len - k]) {
dp[i][j][len] = true;
break;
}
// 第二种情况:S1 -> T2, S2 -> T1
// S1 起点 i,T2 起点 j + 前面那段长度 len-k ,S2 起点 i + 前面长度k
if (dp[i][j + len - k][k] && dp[i + k][j][len - k]) {
dp[i][j][len] = true;
break;
}
}
}
}
}
return dp[0][0][n];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
class Solution {
public boolean isScramble(String s1, String s2) {
// 长度不等,必定不能变换
if (s1.length() != s2.length()) {
return false;
}
// 长度相等,先特判下
if (s1.equals(s2)) {
return true;
}
// 看一下字符个数是否一致,不同直接return false
int n = s1.length();
HashMap<Character, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
char c1 = s1.charAt(i);
char c2 = s2.charAt(i);
map.put(c1, map.getOrDefault(c1, 0) + 1);
map.put(c2, map.getOrDefault(c2, 0) - 1);
}
for (Character key : map.keySet()) {
if (map.get(key) != 0) {
return false;
}
}
// 相同的话,开始判断判断,满足一个就能 return true
for (int i = 1; i < n; i++) {
boolean flag =
// S1 -> T1,S2 -> T2
(isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))) ||
// S1 -> T2,S2 -> T1
(isScramble(s1.substring(0, i), s2.substring(n - i)) && isScramble(s1.substring(i), s2.substring(0, s2.length() - i)));
if (flag) {
return true;
}
}
return false;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
② 朴素解法(TLE)
- 一个朴素的做法根据「扰乱字符串」的生成规则进行判断,由于题目说了整个生成「扰乱字符串」的过程是通过「递归」来进行。要实现 isScramble 函数的作用是判断 s1 是否可以生成出 s2。
- 这样判断的过程,同样我们可以使用「递归」来做:假设 s1 的长度为 n, 的第一次分割的分割点为 i,那么 s1 会被分成 [0,i) 和 [i,n) 两部分。同时由于生成「扰乱字符串」时,可以选交换也可以选不交换,因此我们的 s2 会有两种可能性:
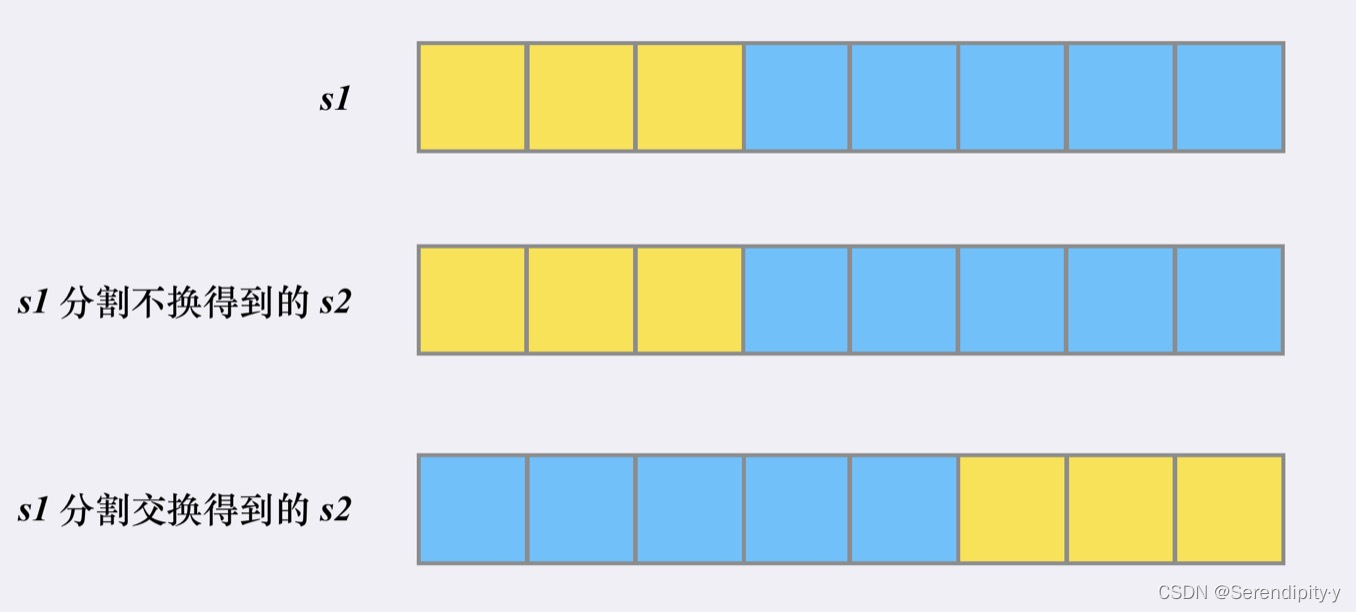
- 因为对于某个确定的分割点,s1 固定分为两部分,分别为 [0,i) & [i,n)。而 s2 可能会有两种分割方式,分别 [0,i) & [i,n) 和 [0,n−i) & [n−i,n)。
- 只需要递归调用 isScramble 检查 s1 的 [0,i) & [i,n) 部分能否与 「s2 的 [0,i) & [i,n)」 或者 「s2 的 [0,n−i) & [n−i,n)」 匹配即可。
- 同时,将「s1 和 s2 相等」和「s1 和 s2 词频不同」作为「递归」出口。
- Java 示例:
class Solution {
public boolean isScramble(String s1, String s2) {
if (s1.equals(s2)) return true;
if (!check(s1, s2)) return false;
int n = s1.length();
for (int i = 1; i < n; i++) {
// s1 的 [0,i) 和 [i,n)
String a = s1.substring(0, i), b = s1.substring(i);
// s2 的 [0,i) 和 [i,n)
String c = s2.substring(0, i), d = s2.substring(i);
if (isScramble(a, c) && isScramble(b, d)) return true;
// s2 的 [0,n-i) 和 [n-i,n)
String e = s2.substring(0, n - i), f = s2.substring(n - i);
if (isScramble(a, f) && isScramble(b, e)) return true;
}
return false;
}
// 检查 s1 和 s2 词频是否相同
boolean check(String s1, String s2) {
if (s1.length() != s2.length()) return false;
int n = s1.length();
int[] cnt1 = new int[26], cnt2 = new int[26];
char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
for (int i = 0; i < n; i++) {
cnt1[cs1[i] - 'a']++;
cnt2[cs2[i] - 'a']++;
}
for (int i = 0; i < 26; i++) {
if (cnt1[i] != cnt2[i]) return false;
}
return true;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122887791
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)