【数据结构与算法】之“寻找两个正序数组的中位数”的求解思路和算法示例

一、题目要求

• 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2，请找出并返回这两个正序数组的中位数 。
• 算法的时间复杂度应该为 O(log (m+n)) 。
• 示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

  

 

  
1
  
2
  
3
 

• 示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

  

 

  
1
  
2
  
3
 

• 示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

  

 

  
1
  
2
 

• 示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

  

 

  
1
  
2
 

• 示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

  

 

  
1
  
2
 

• 提示：
• • nums1.length == m
• • nums2.length == n
• • 0 <= m <= 1000
• • 0 <= n <= 1000
• • 1 <= m + n <= 2000
• • -106 <= nums1[i], nums2[i] <= 106

二、求解算法

① 解法一

• 简单粗暴，先将两个数组合并，两个有序数组的合并也是归并排序中的一部分。
• 然后根据奇数，还是偶数，返回中位数。
• Java 示例：

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int[] nums;
    int m = nums1.length;
    int n = nums2.length;
    nums = new int[m + n];
    if (m == 0) {
        if (n % 2 == 0) {
            return (nums2[n / 2 - 1] + nums2[n / 2]) / 2.0;
        } else {
            return nums2[n / 2];
        }
    }
    if (n == 0) {
        if (m % 2 == 0) {
            return (nums1[m / 2 - 1] + nums1[m / 2]) / 2.0;
        } else {
            return nums1[m / 2];
        }
    }

    int count = 0;
    int i = 0, j = 0;
    while (count != (m + n)) {
        if (i == m) {
            while (j != n) {
                nums[count++] = nums2[j++];
            }
            break;
        }
        if (j == n) {
            while (i != m) {
                nums[count++] = nums1[i++];
            }
            break;
        }

        if (nums1[i] < nums2[j]) {
            nums[count++] = nums1[i++];
        } else {
            nums[count++] = nums2[j++];
        }
    }

    if (count % 2 == 0) {
        return (nums[count / 2 - 1] + nums[count / 2]) / 2.0;
    } else {
        return nums[count / 2];
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
 

② 解法二

• 其实，不需要将两个数组真的合并，只需要找到中位数在哪里就可以了。
• 开始的思路是写一个循环，然后里边判断是否到了中位数的位置，到了就返回结果，但这里对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后，出了 for 循环对边界的判断也会分几种情况。
• 首先是怎么将奇数和偶数的情况合并一下，用 len 表示合并后数组的长度，如果是奇数，我们需要知道第 （len+1）/2 个数就可以了，如果遍历的话需要遍历 int(len/2 ) + 1 次。如果是偶数，我们需要知道第 len/2和 len/2+1 个数，也是需要遍历 len/2+1 次。所以遍历的话，奇数和偶数都是 len/2+1 次。
• 返回中位数的话，奇数需要最后一次遍历的结果就可以了，偶数需要最后一次和上一次遍历的结果。所以用两个变量 left 和 right，right 保存当前循环的结果，在每次循环前将 right 的值赋给 left。这样在最后一次循环的时候，left 将得到 right 的值，也就是上一次循环的结果，接下来 right 更新为最后一次的结果。
• 循环中该怎么写，什么时候 A 数组后移，什么时候 B 数组后移，用 aStart 和 bStart 分别表示当前指向 A 数组和 B 数组的位置，如果 aStart 还没有到最后并且此时 A 位置的数字小于 B 位置的数组，那么就可以后移了，也就是aStart＜m&&A[aStart]< B[bStart]。
• 但如果 B 数组此刻已经没有数字了，继续取数字 B[ bStart ]，则会越界，所以判断下 bStart 是否大于数组长度了，这样 || 后边的就不会执行了，也就不会导致错误了，所以增加为 aStart＜m&&(bStart) >= n||A[aStart]<B[bStart]) 。
• Java 示例：

public double findMedianSortedArrays(int[] A, int[] B) {
    int m = A.length;
    int n = B.length;
    int len = m + n;
    int left = -1, right = -1;
    int aStart = 0, bStart = 0;
    for (int i = 0; i <= len / 2; i++) {
        left = right;
        if (aStart < m && (bStart >= n || A[aStart] < B[bStart])) {
            right = A[aStart++];
        } else {
            right = B[bStart++];
        }
    }
    if ((len & 1) == 0)
        return (left + right) / 2.0;
    else
        return right;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
 

③ 解法三

• 上边的两种思路，时间复杂度都达不到题目的要求 O(log(m+n)。看到 log，很明显，只有用到二分的方法才能达到，不妨用另一种思路，题目是求中位数，其实就是求第 k 小数的一种特殊情况，而求第 k 小数有一种算法。
• 解法二中，我们一次遍历就相当于去掉不可能是中位数的一个值，也就是一个一个排除。由于数列是有序的，其实完全可以一半儿一半儿的排除，假设要找第 k 小数，可以每次循环排除掉 k/2 个数。
• 假设要找第 7 小的数字：

• 比较两个数组的第 k/2 个数字，如果 k 是奇数，向下取整，也就是比较第 3 个数字，上边数组中的4 和下边数组中的 3，如果哪个小，就表明该数组的前 k/2 个数字都不是第 k 小数字，所以可以排除。也就是 1，2，3 这三个数字不可能是第 7 小的数字，可以把它排除掉。将 1349 和 45678910 两个数组作为新的数组进行比较。
• 更一般的情况 A[1] ，A[2] ，A[3]，A[k/2] … ，B[1]，B[2]，B[3]，B[k/2] … ，如果 A[k/2]<B[k/2] ，那么A[1]，A[2]，A[3]，A[k/2] 都不可能是第 k 小的数字。
• A 数组中比 A[k/2] 小的数有 k/2-1 个，B 数组中，B[k/2] 比 A[k/2] 小，假设 B[k/2] 前边的数字都比 A[k/2] 小，也只有 k/2-1 个，所以比 A[k/2] 小的数字最多有 k/1-1+k/2-1=k-2个，所以 A[k/2] 最多是第 k-1 小的数。而比 A[k/2] 小的数更不可能是第 k 小的数了，所以可以把它们排除。
• 橙色的部分表示已经去掉的数字：

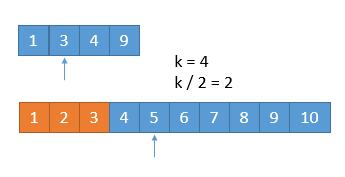
• 由于已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4，此时两个数组，比较第 2 个数字，3 < 5，所以可以把小的那个数组中的 1 ，3 排除掉了：

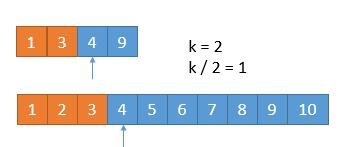
• 我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4，怎么办呢？由于两个数相等，所以无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，就假设 4 > 4 吧，所以此时将下边的 4 去掉：

• 由于又去掉 1 个数字，此时要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4，所以第 7 小的数字是 4。
• 每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候：

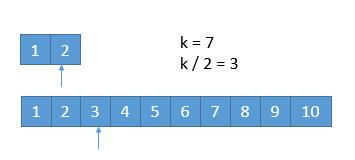
• 此时 k / 2 等于 3，而上边的数组长度是 2，此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3，所以就会导致上边的数组 1，2 都被排除，造成下边的情况：

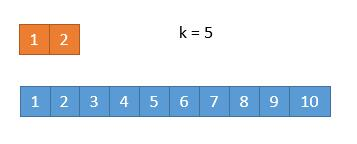
• 由于 2 个元素被排除，所以此时 k = 5，又由于上边的数组已经空了，只需要返回下边的数组的第 5 个数字就可以了。
• 从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。
• 所以采用递归的思路，为了防止数组长度小于 k/2，所以每次比较 min(k/2，len(数组) 对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且 k 要减去排除的数字的个数，递归出口就是当 k=1 或者其中一个数字长度是 0 了。
• Java 示例：

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        // 因为数组是从索引0开始的，因此我们在这里必须+1，即索引(k+1)的数，才是第k个数。
        int left = (n + m + 1) / 2;
        int right = (n + m + 2) / 2;
        // 将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k
        return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
    }
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        // 因为索引和算数不同6-0=6，但是是有7个数的，因为end初始就是数组长度-1构成的。
        // 最后len代表当前数组(也可能是经过递归排除后的数组)，符合当前条件的元素的个数
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        // 让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1
        // 就是如果len1长度小于len2，把getKth()中参数互换位置，即原来的len2就变成了len1，即len1，永远比len2小
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        // 如果一个数组中没有了元素，那么即从剩余数组nums2的其实start2开始加k再-1.
        // 因为k代表个数，而不是索引，那么从nums2后再找k个数，那个就是start2 + k-1索引处就行了。因为还包含nums2[start2]也是一个数。因为它在上次迭代时并没有被排除
        if (len1 == 0) return nums2[start2 + k - 1];

        // 如果k=1，表明最接近中位数了，即两个数组中start索引处，谁的值小，中位数就是谁(start索引之前表示经过迭代已经被排出的不合格的元素，即数组没被抛弃的逻辑上的范围是nums[start]--->nums[end])。
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);

        // 为了防止数组长度小于 k/2,每次比较都会从当前数组所生长度和k/2作比较，取其中的小的(如果取大的，数组就会越界)
        // 然后素组如果len1小于k / 2，表示数组经过下一次遍历就会到末尾，然后后面就会在那个剩余的数组中寻找中位数
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        // 如果nums1[i] > nums2[j]，表示nums2数组中包含j索引，之前的元素，逻辑上全部淘汰，即下次从J+1开始。
        // 而k则变为k - (j - start2 + 1)，即减去逻辑上排出的元素的个数(要加1，因为索引相减，相对于实际排除的时要少一个的)
        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        } else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

文章来源: blog.csdn.net，作者：Serendipity·y，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Forever_wj/article/details/122441115