【数据机构与算法】之深入解析“恢复二叉搜索树”的求解思路与算法示例
【摘要】
一、题目要求
给你二叉搜索树的根节点 root ,该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树。示例 1:
输入:root = [1,3,null,null,2]
输...
一、题目要求
- 给你二叉搜索树的根节点 root ,该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树。
- 示例 1:

输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
- 1
- 2
- 3
- 示例 2:
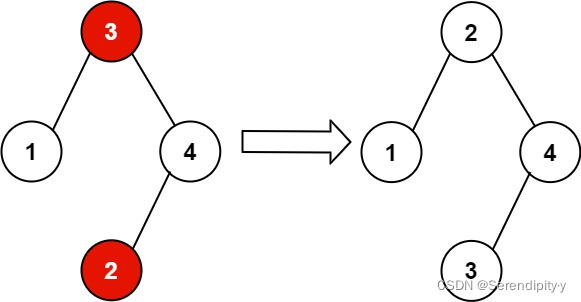
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
- 1
- 2
- 3
- 提示:
-
- 树上节点的数目在范围 [2, 1000] 内;
-
- -231 <= Node.val <= 231 - 1。
二、求解算法
① 扫描遍历
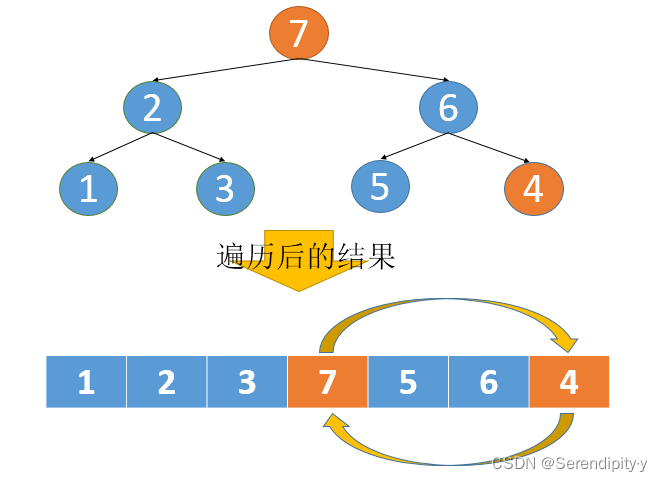
- 由于是二叉搜索树,这就是意味着节点之间是有顺序关系的,如果把整棵树都遍历一遍,将遍历的结果保存下来,比如放到一个数组中,那么这个数组应该是有序的。
- 既然是有序的那就很好处理了,我们将这个有序的数组遍历一遍,如果数组是完全有序的,那么直接返回就可以了;否则,找到顺序不一致的两个下标 i 和 j,将 arr[i].val 和 arr[j].val 的值互换一下即可。
- Java 示例:
class Solution {
public void recoverTree(TreeNode root) {
List<TreeNode> list = new ArrayList<TreeNode>();
dfs(root,list);
TreeNode x = null;
TreeNode y = null;
// 扫描遍历的结果,找出可能存在错误交换的节点x和y
for(int i=0;i<list.size()-1;++i) {
if(list.get(i).val>list.get(i+1).val) {
y = list.get(i+1);
if(x==null) {
x = list.get(i);
}
}
}
// 如果x和y不为空,则交换这两个节点值,恢复二叉搜索树
if(x!=null && y!=null) {
int tmp = x.val;
x.val = y.val;
y.val = tmp;
}
}
// 中序遍历二叉树,并将遍历的结果保存到list中
private void dfs(TreeNode node,List<TreeNode> list) {
if(node==null) {
return;
}
dfs(node.left,list);
list.add(node);
dfs(node.right,list);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- Python 示例:
class Solution(object):
def recoverTree(self, root):
nodes = []
# 中序遍历二叉树,并将遍历的结果保存到list中
def dfs(root):
if not root:
return
dfs(root.left)
nodes.append(root)
dfs(root.right)
dfs(root)
x = None
y = None
pre = nodes[0]
# 扫描遍历的结果,找出可能存在错误交换的节点x和y
for i in xrange(1,len(nodes)):
if pre.val>nodes[i].val:
y=nodes[i]
if not x:
x = pre
pre = nodes[i]
# 如果x和y不为空,则交换这两个节点值,恢复二叉搜索树
if x and y:
x.val,y.val = y.val,x.val
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
② 中序遍历
- 解法①中,利用了额外的数组保存了遍历的结果,如果后面一个数比前面一个数小,那就找到了要交换的节点。
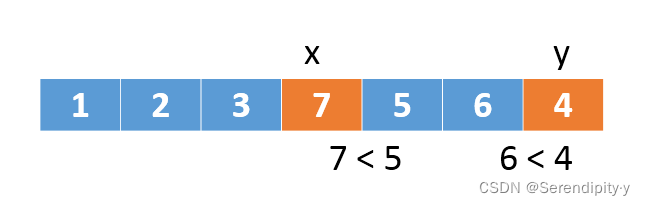
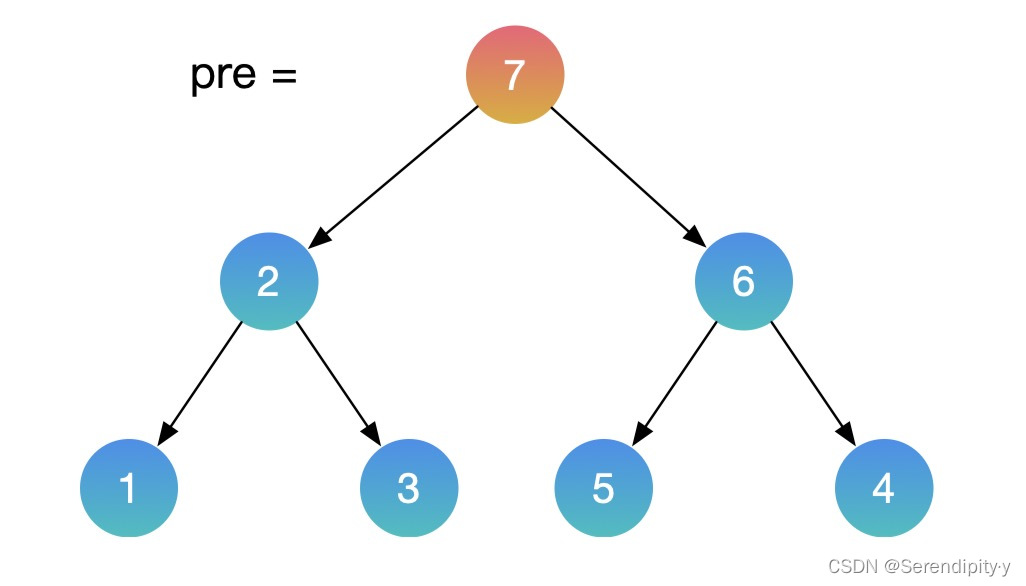
- 按照同样的思路,用中序遍历的方式遍历这颗二叉搜索树,再增加一个辅助的 pre 指针,记录上一个节点的值。如果当前节点的值,小于上一个节点的值,这就找到了需要交换的节点。利用这种方式,就不需要额外的数组空间了。
- 整个过程如下所示:
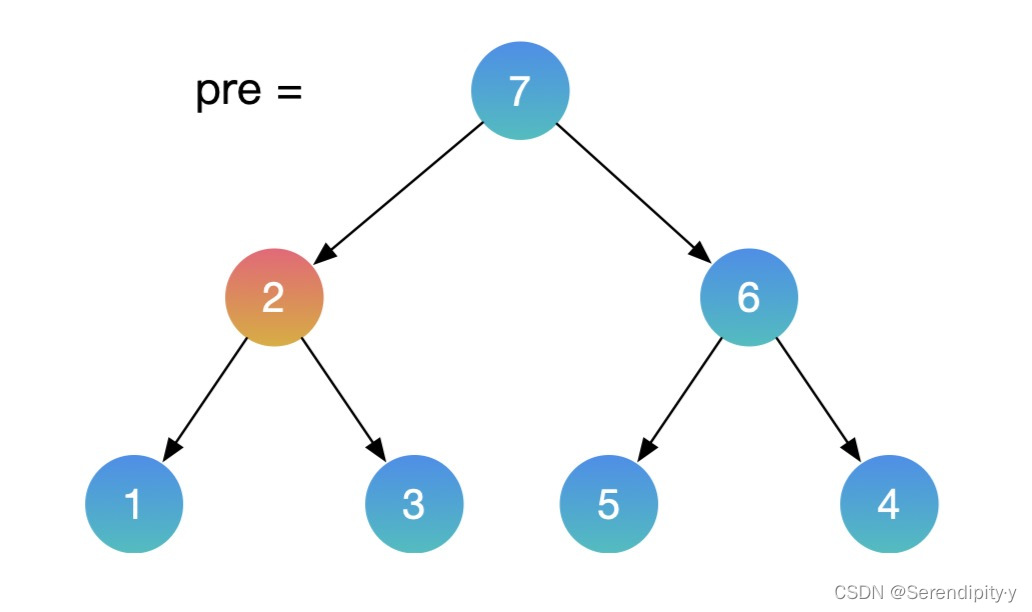
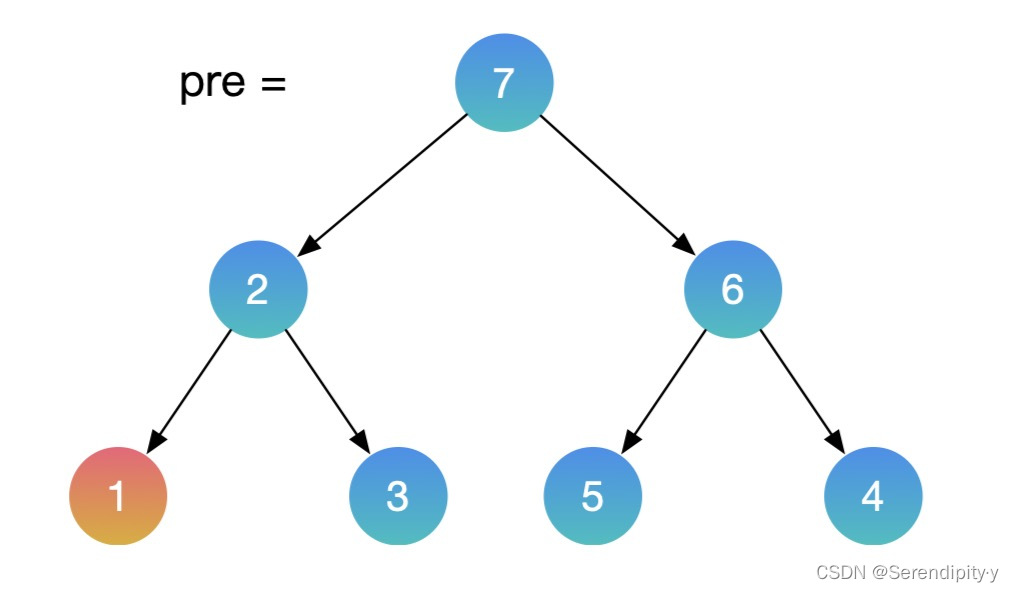
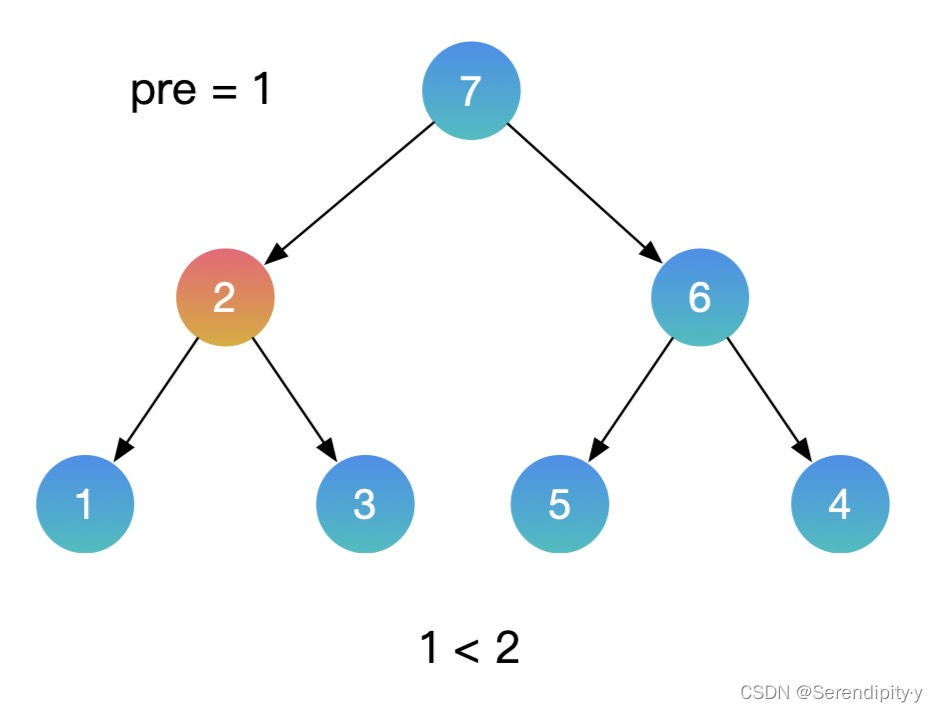
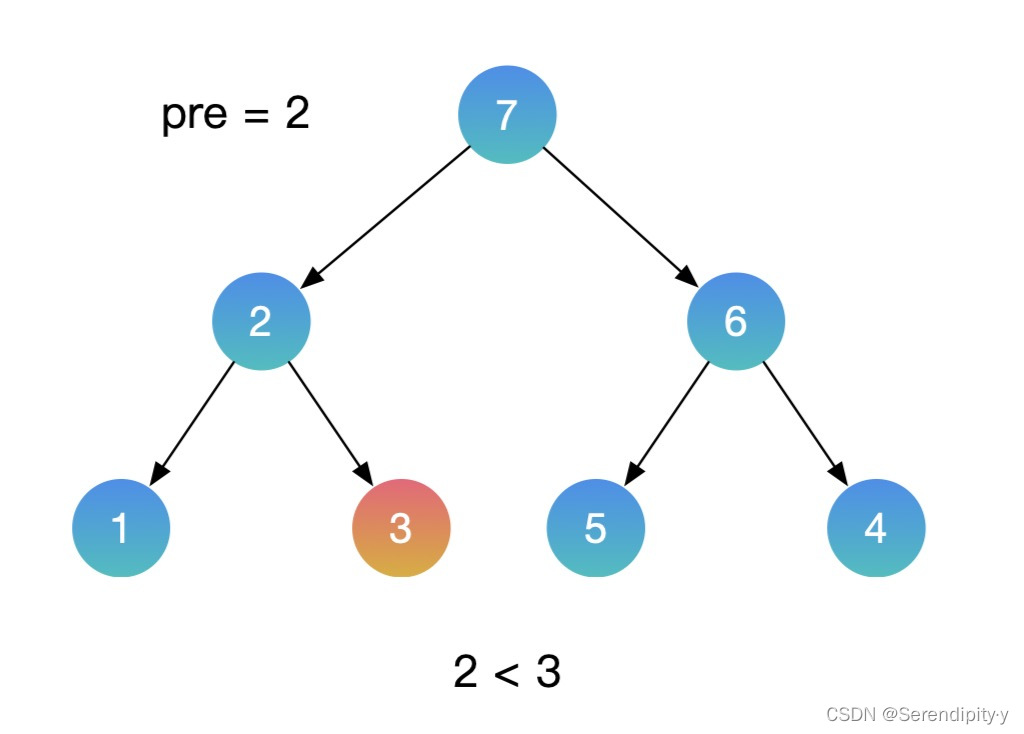
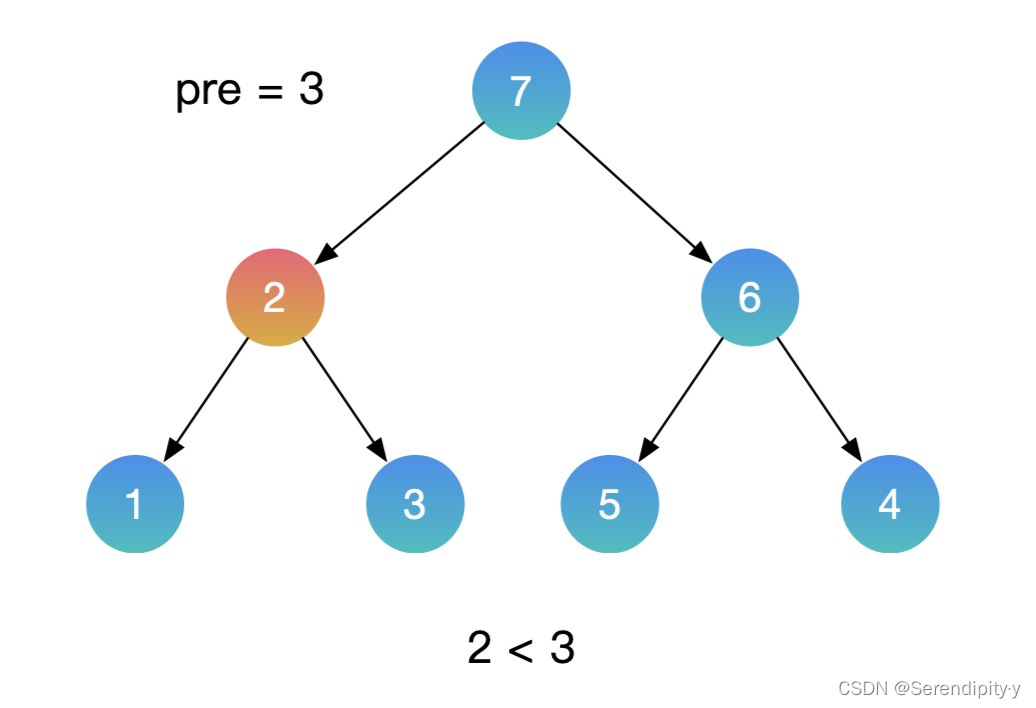
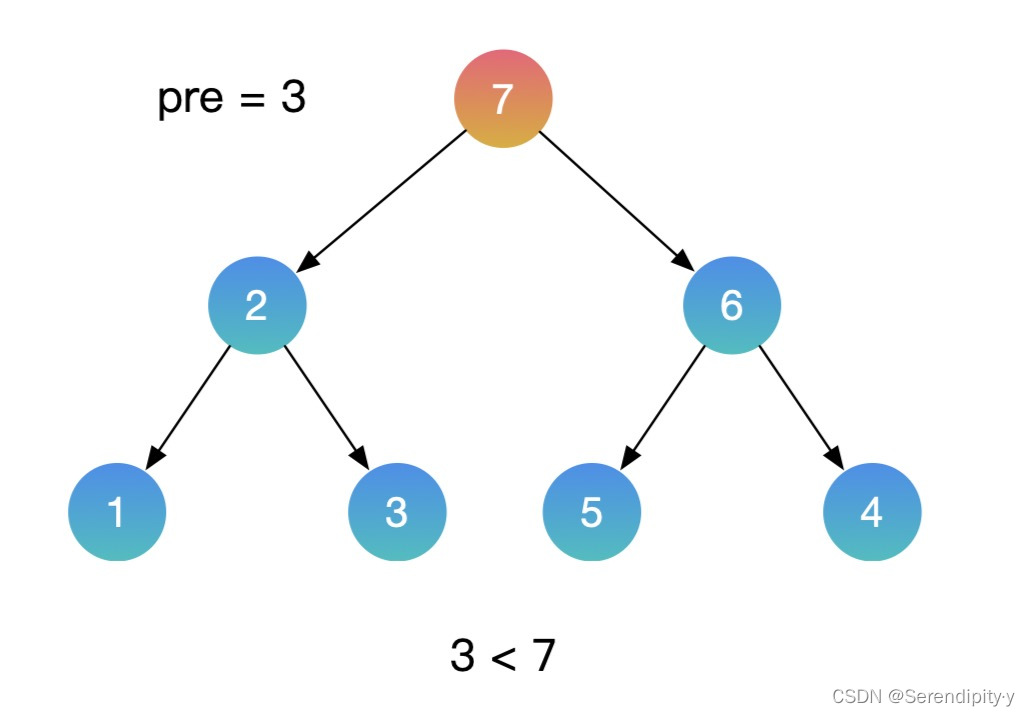
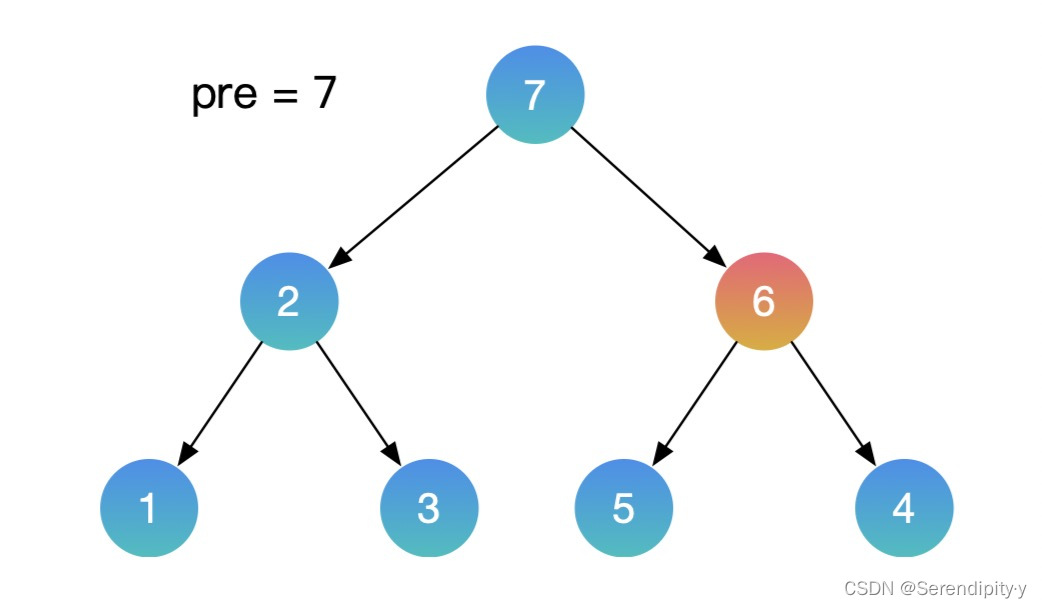
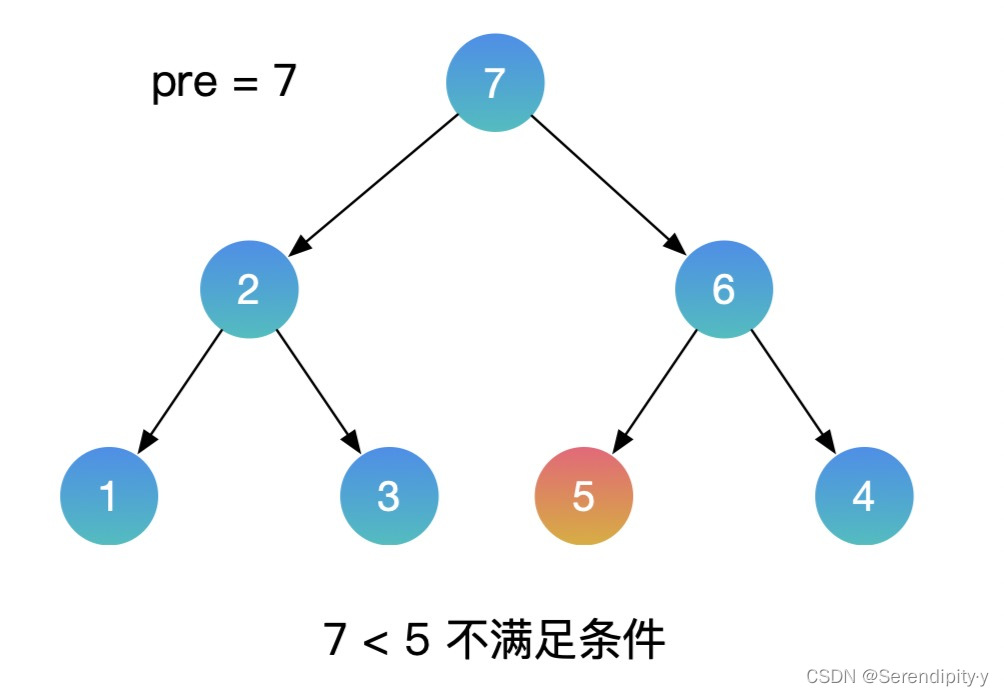
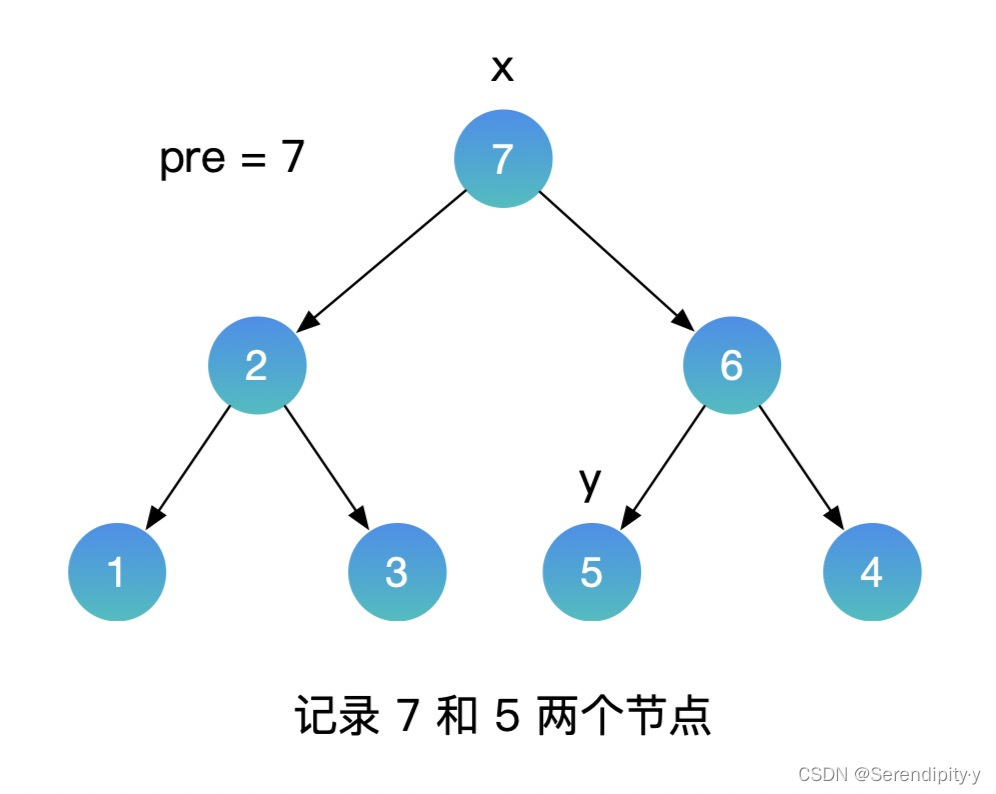
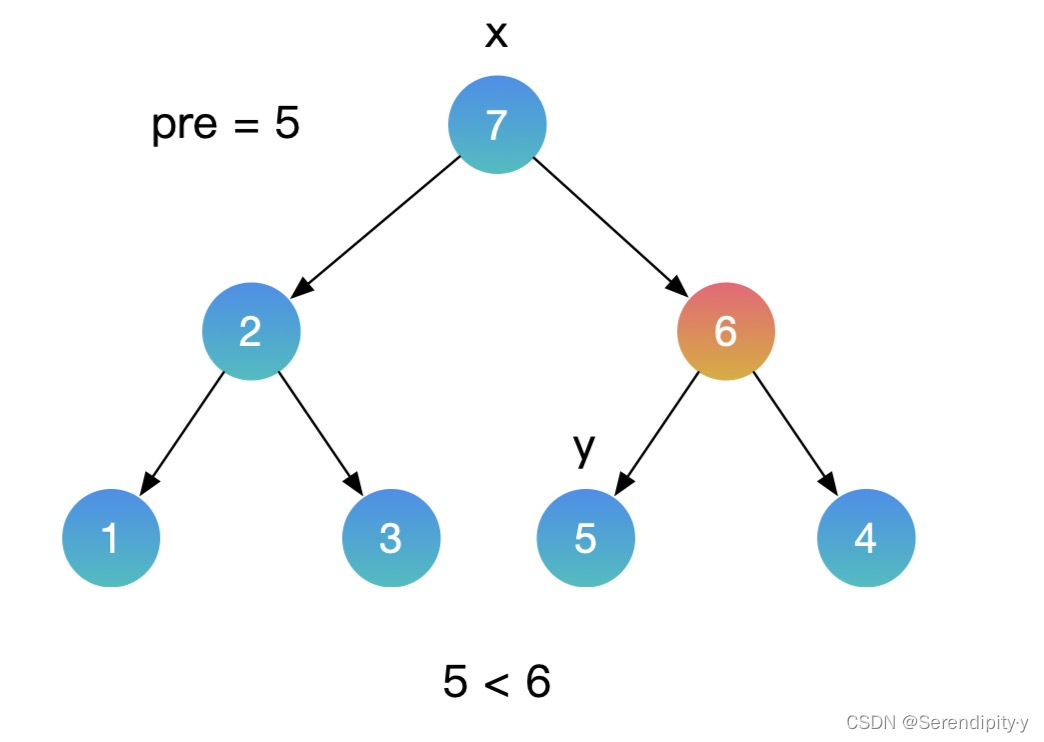
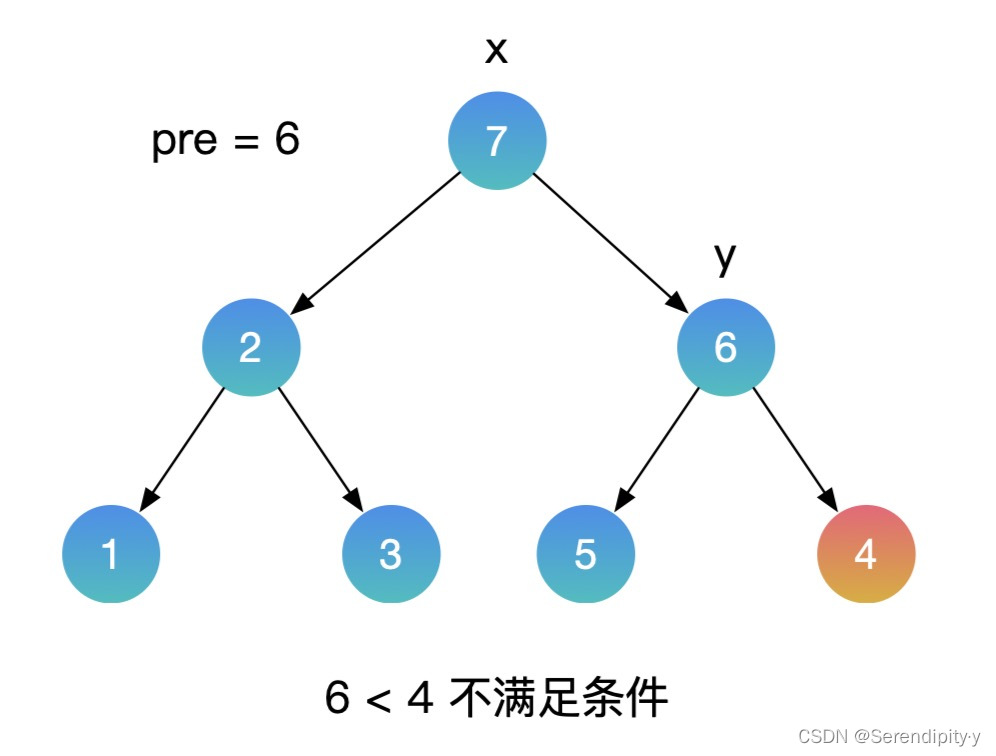
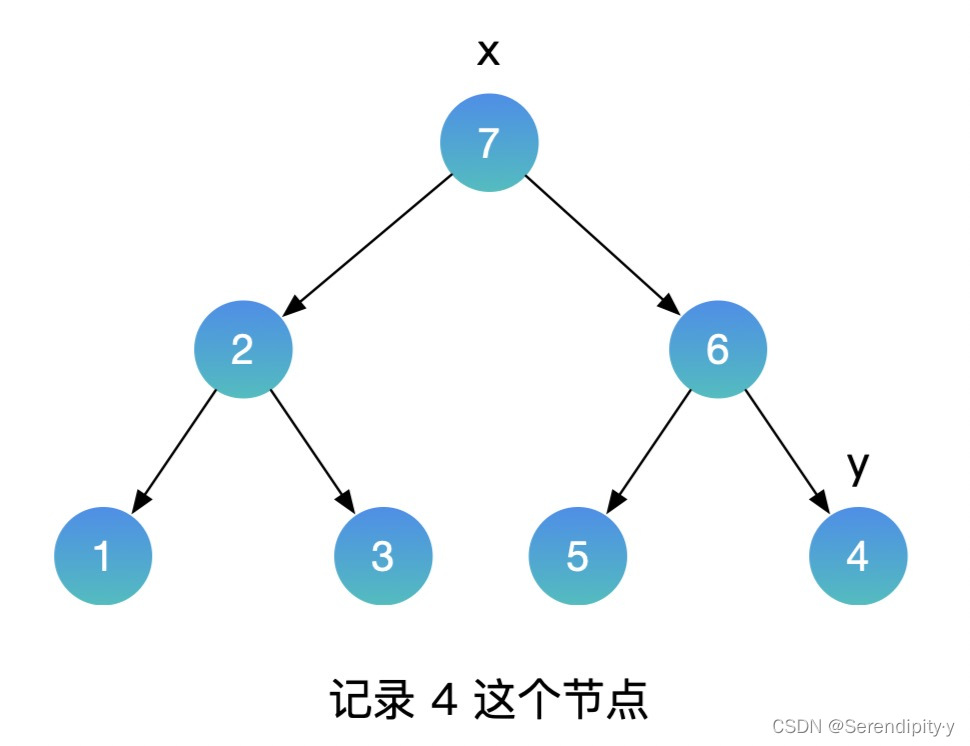
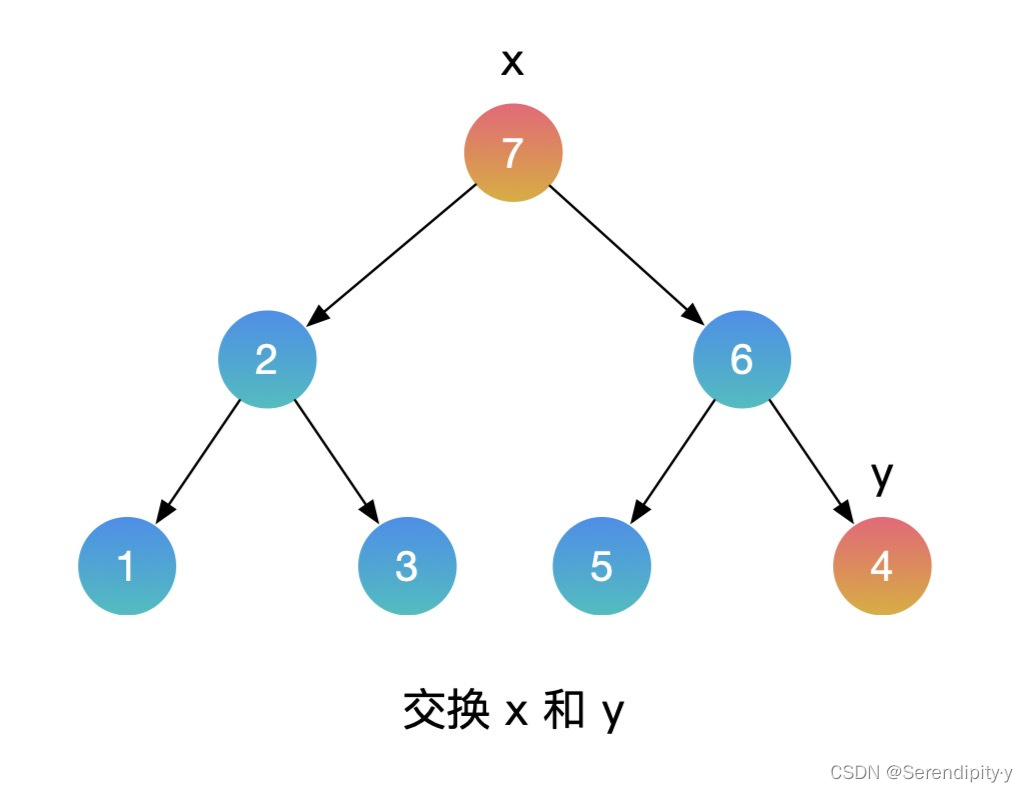
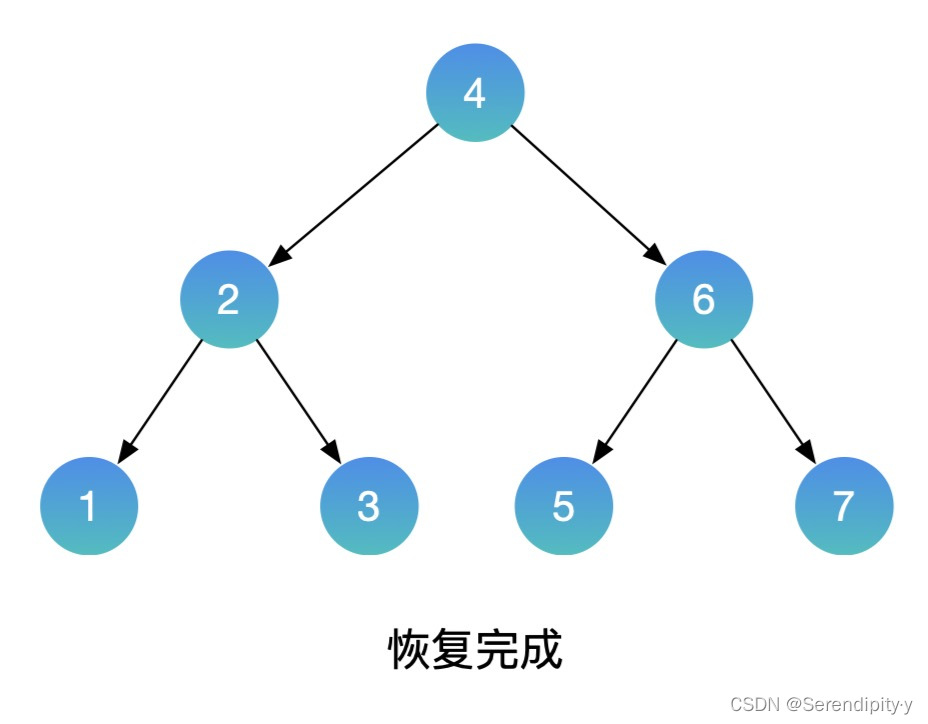
- Java 示例:
class Solution {
// 用两个变量x,y来记录需要交换的节点
private TreeNode x = null;
private TreeNode y = null;
private TreeNode pre = null;
public void recoverTree(TreeNode root) {
dfs(root);
// 如果x和y都不为空,说明二叉搜索树出现错误的节点,将其交换
if(x!=null && y!=null) {
int tmp = x.val;
x.val = y.val;
y.val = tmp;
}
}
// 中序遍历二叉树,并比较上一个节点(pre)和当前节点的值,如果pre的值大于当前节点值,则记录下这两个节点
private void dfs(TreeNode node) {
if(node==null) {
return;
}
dfs(node.left);
if(pre==null) {
pre = node;
}
else {
if(pre.val>node.val) {
y = node;
if(x==null) {
x = pre;
}
}
pre = node;
}
dfs(node.right);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- Python 示例:
class Solution(object):
def recoverTree(self, root):
# 用两个变量x,y来记录需要交换的节点
self.x = None
self.y = None
self.pre = None
# 中序遍历二叉树,并比较上一个节点(pre)和当前节点的值,如果pre的值大于当前节点值,则记录下这两个节点
def dfs(root):
if not root:
return
dfs(root.left)
if not self.pre:
self.pre = root
else:
if self.pre.val>root.val:
self.y = root
if not self.x:
self.x = self.pre
self.pre = root
dfs(root.right)
dfs(root)
# 如果x和y都不为空,说明二叉搜索树出现错误的节点,将其交换
if self.x and self.y:
self.x.val,self.y.val = self.y.val,self.x.val
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
③ 莫里斯遍历
- 解法②还不是真正的常数空间复杂度,想要达到常数空间,可以用“莫里斯遍历”,这种方式可以做到 O(1) 的空间复杂度去遍历一棵树。
- 回想一下中序遍历的递归版本,也就是一路往左走到底,左边走不通,再往右边走:
dfs(root.left)
打印节点 root
dfs(root.right)
- 1
- 2
- 3
- 如下所示,就是 4->3->1 这个过程,一路往左,走不通了再往右,也就是遍历 2:
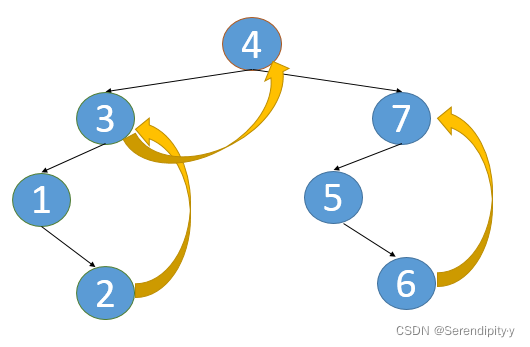
- 当然如果 2 的右边还有节点那么还会继续遍历下去。现在 2 的右边已经是空,对于递归来说操作系统自动出栈,然后会访问 3 这个节点。
- 既然 2 是叶子节点,左右子树都是空,可以利用这个空闲出来的信息,将 2 的右子树指向 3,这样当 2 遍历完后,再往右走,就会自动走到 3 这个节点。
- 同理,将 3 的右子树指向 4,将 6 的右子树指向 7。
- 这样的话,就可以省去额外的栈空间,利用叶子节点的右子树这个特点,将其重新赋予指向关系 ,就是莫里斯遍历的核心了。不过光是这样还不行,再回看上图,其实已经不是一棵树了,而是变成图,因为出现了循环。所以还需要将新加这个指向关系给去掉。
- 如下所示,假设已经遍历到 4 这个节点,那就意味着 4 在左子树都遍历完,对应的就是 1,2,3 都遍历完:
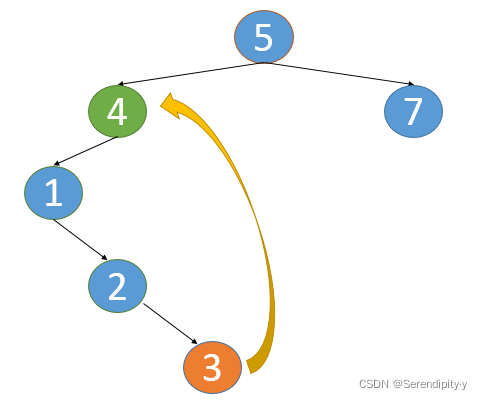
- 3.right=4 这个是新加上的,既然现在已经遍历到 4,就可以将 3.right=null,将这个指向关系还原即可。从上图中也可以看出,所谓新加的指向关系,就是找到根节点左子树的最右子树,然后将最右子树的 right 指向根节点。
- 完整执行过程如下:
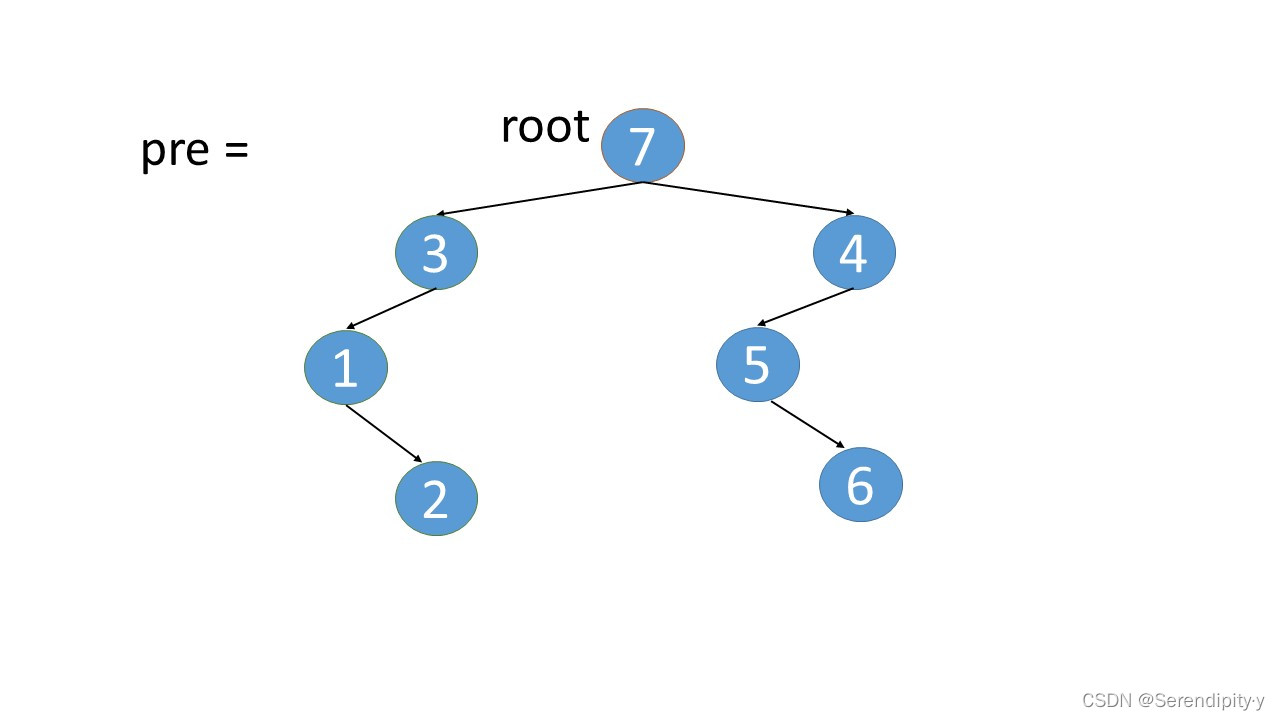
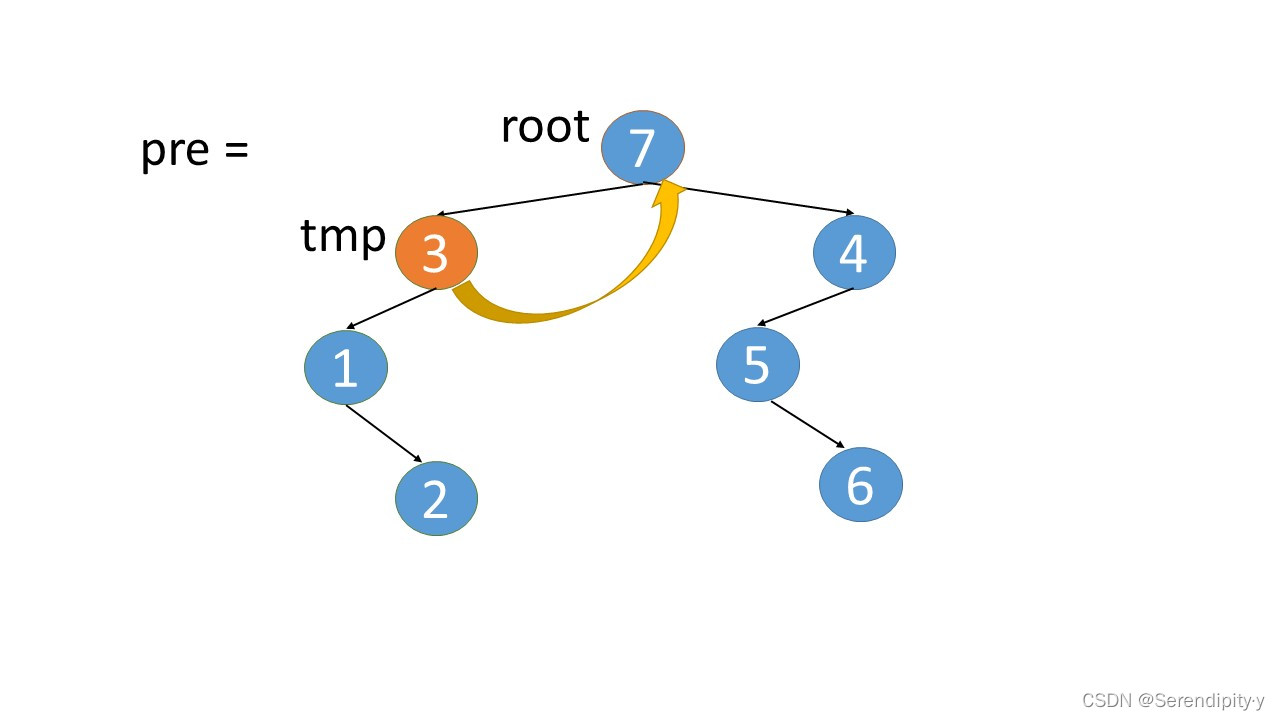
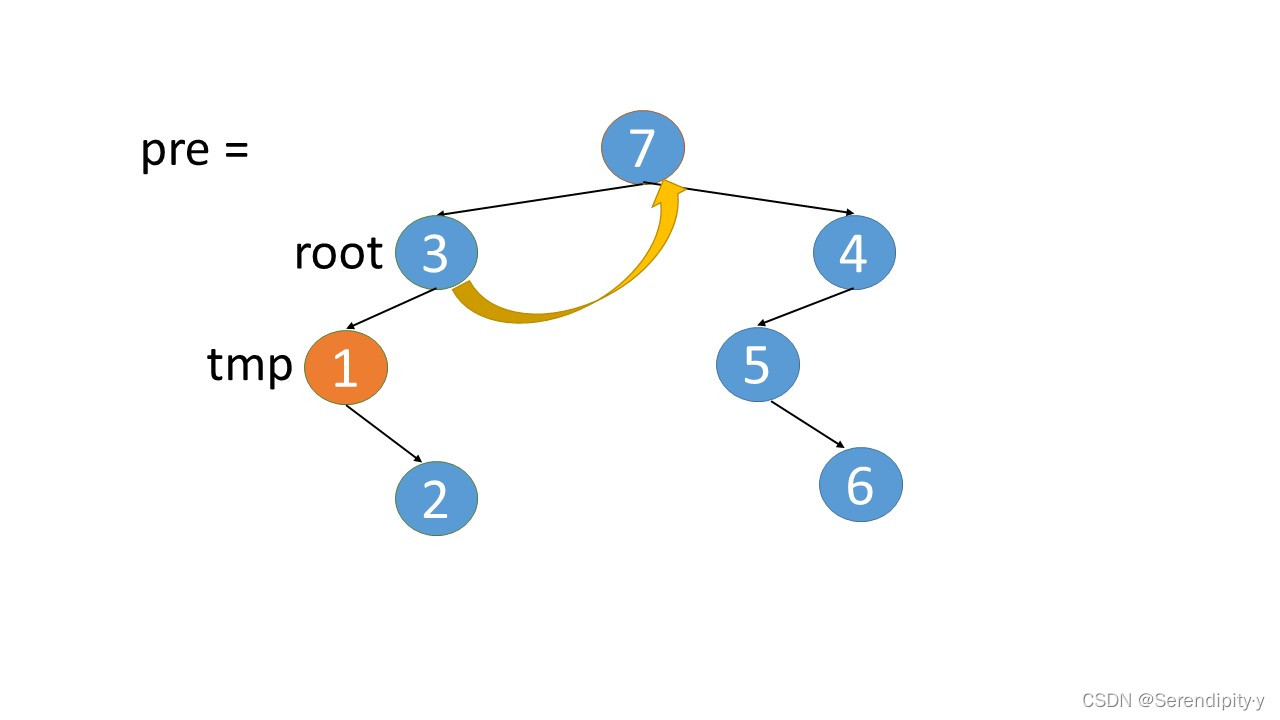
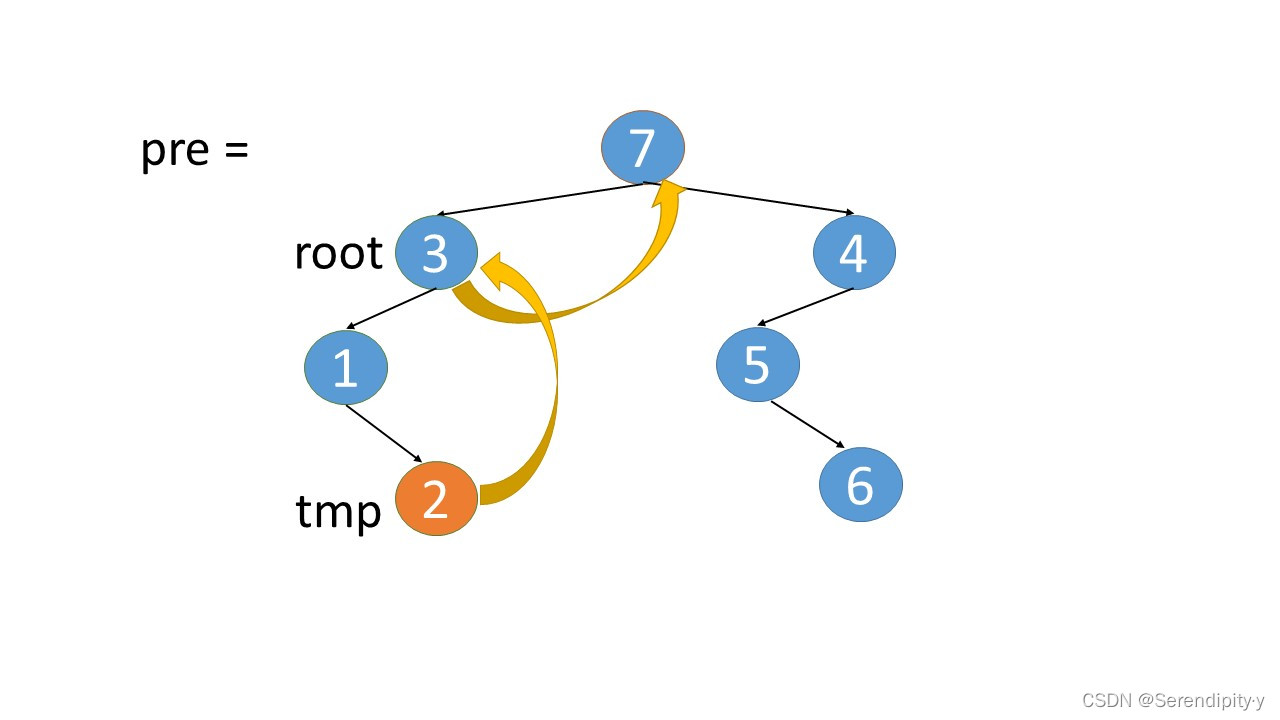
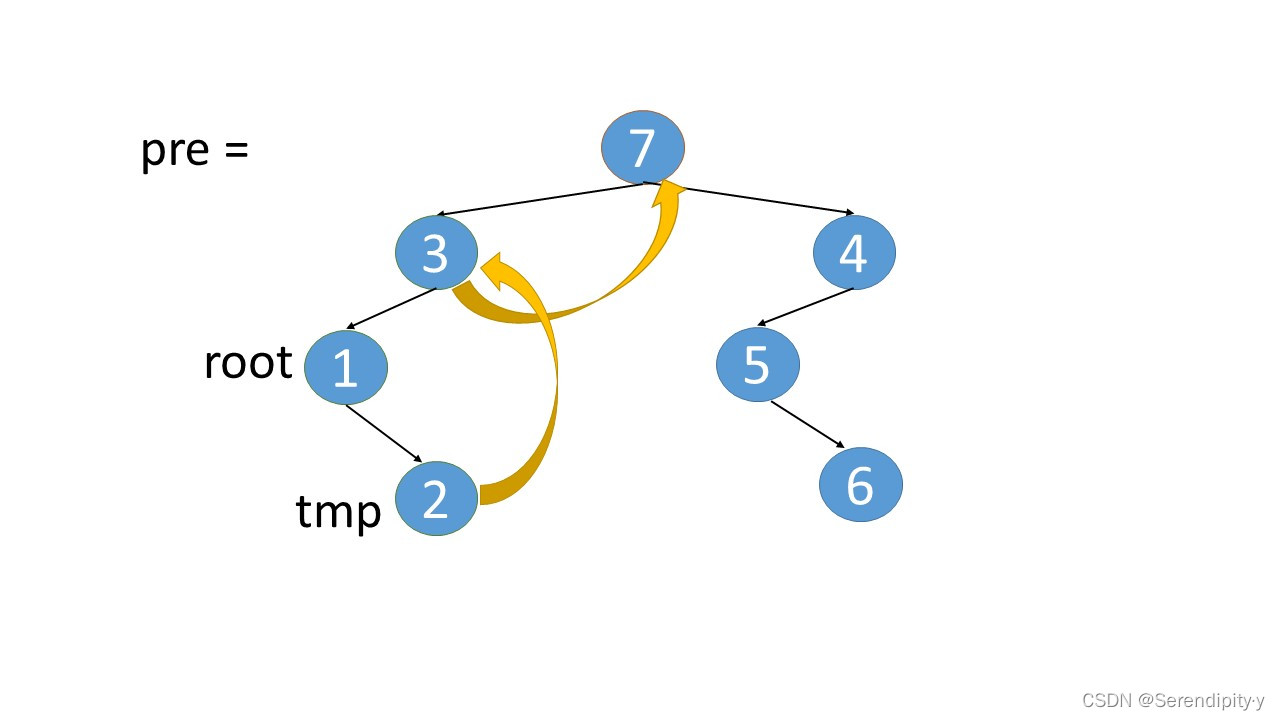
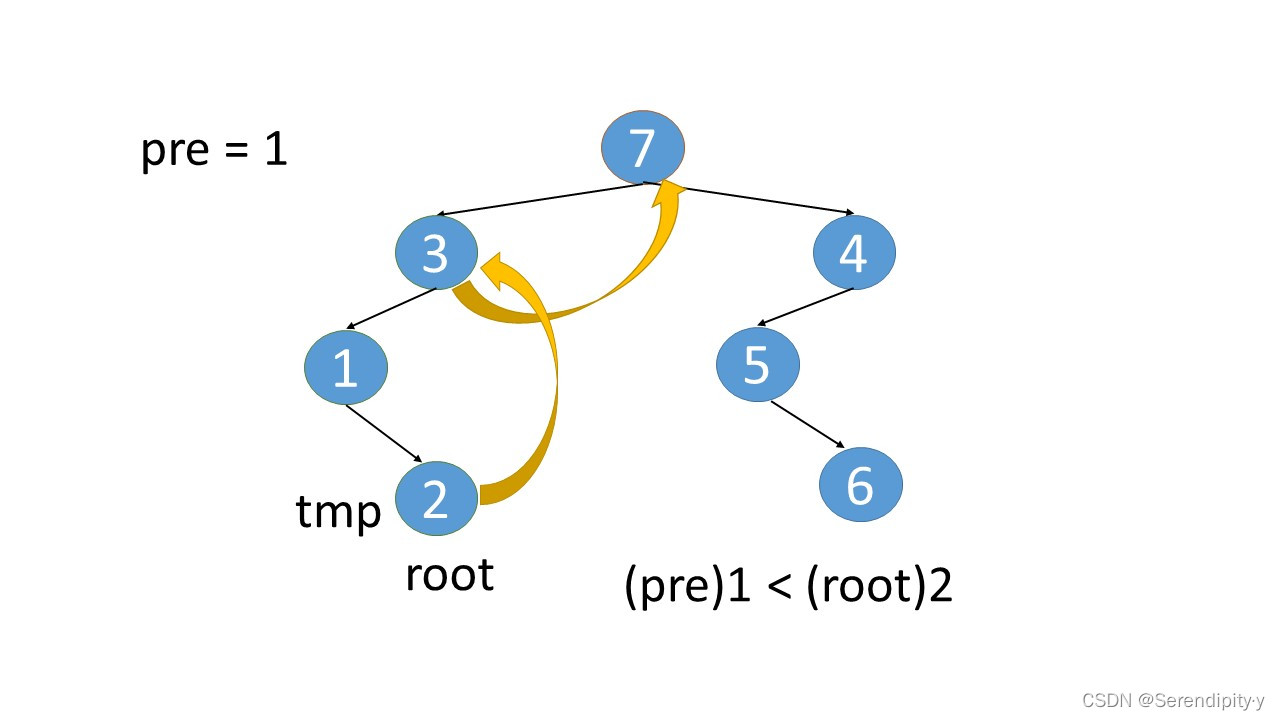
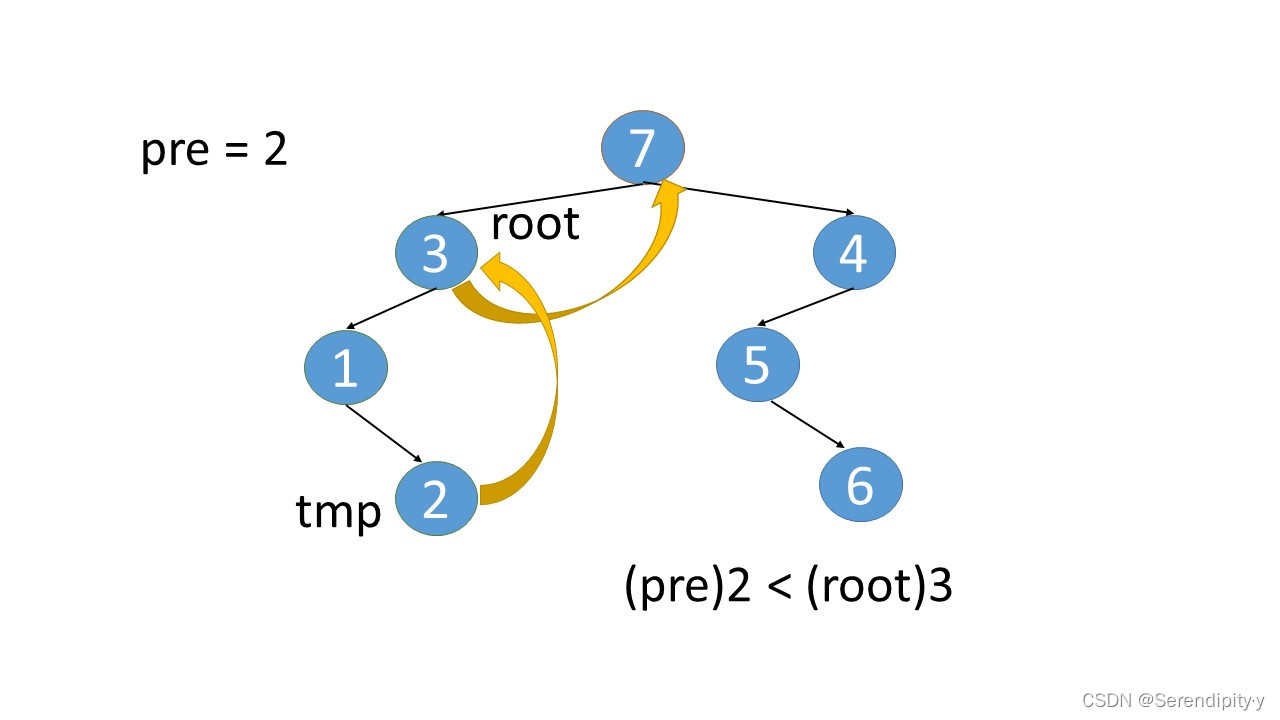
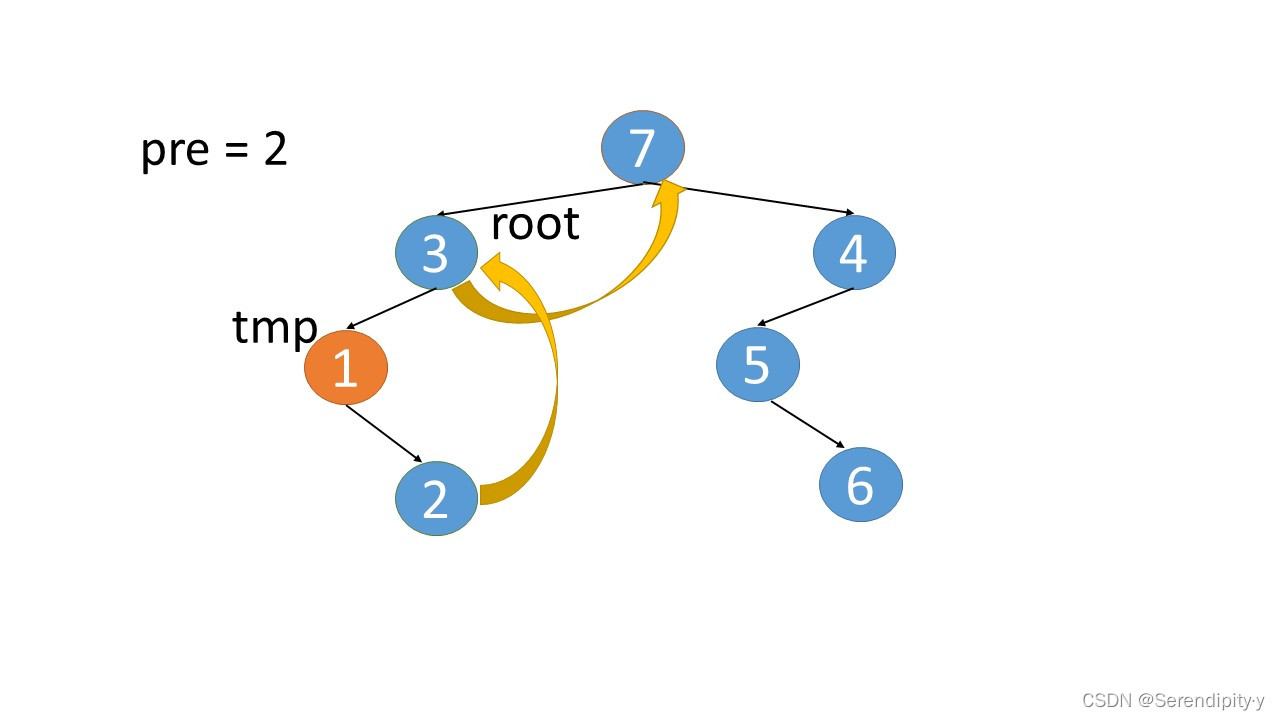
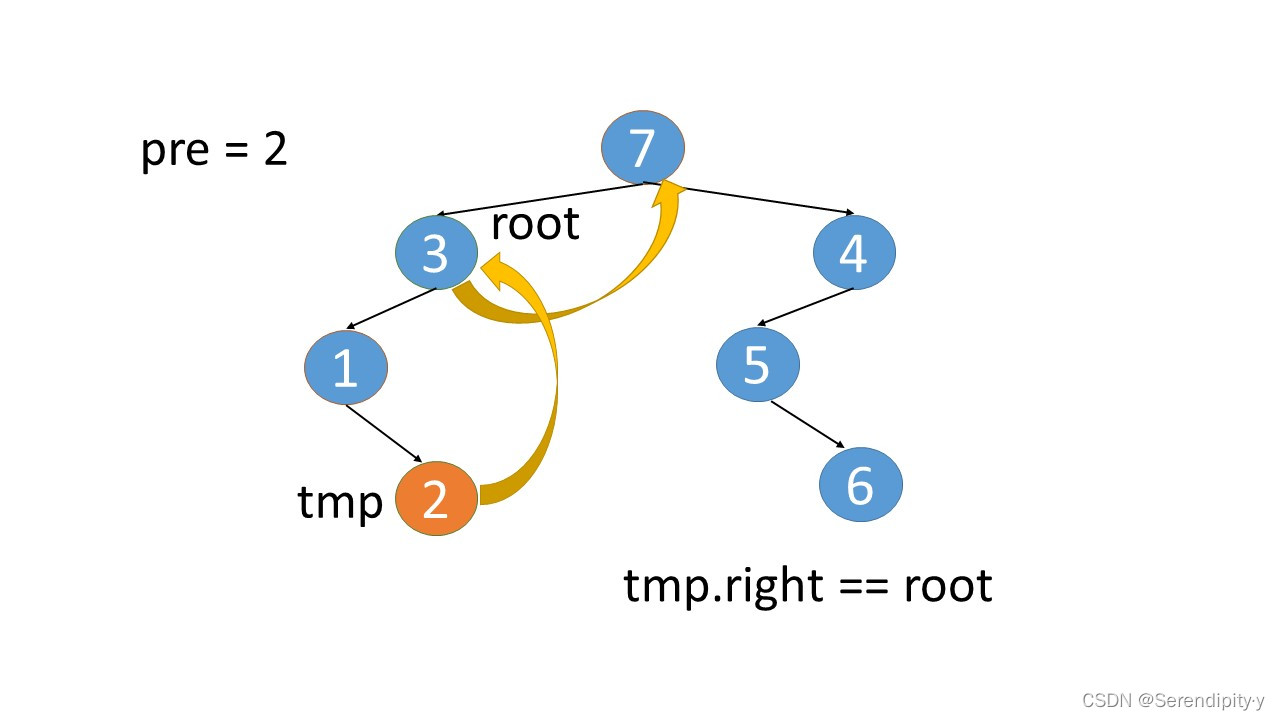
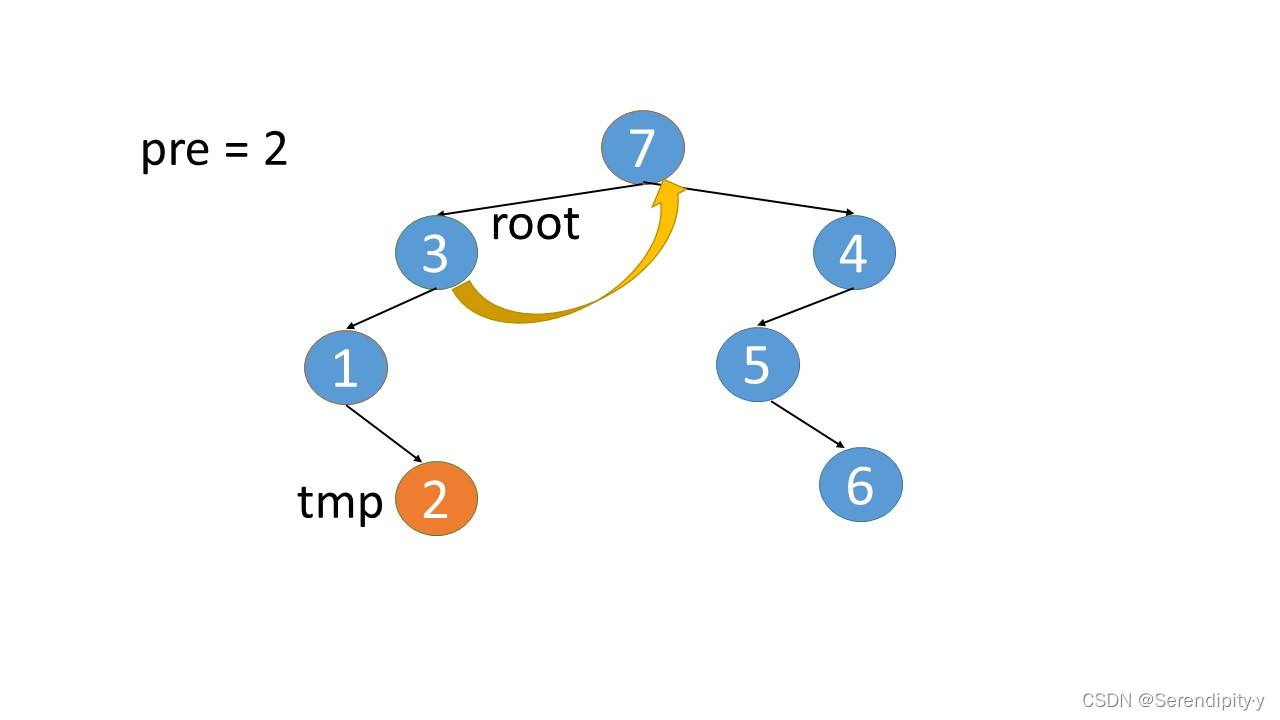
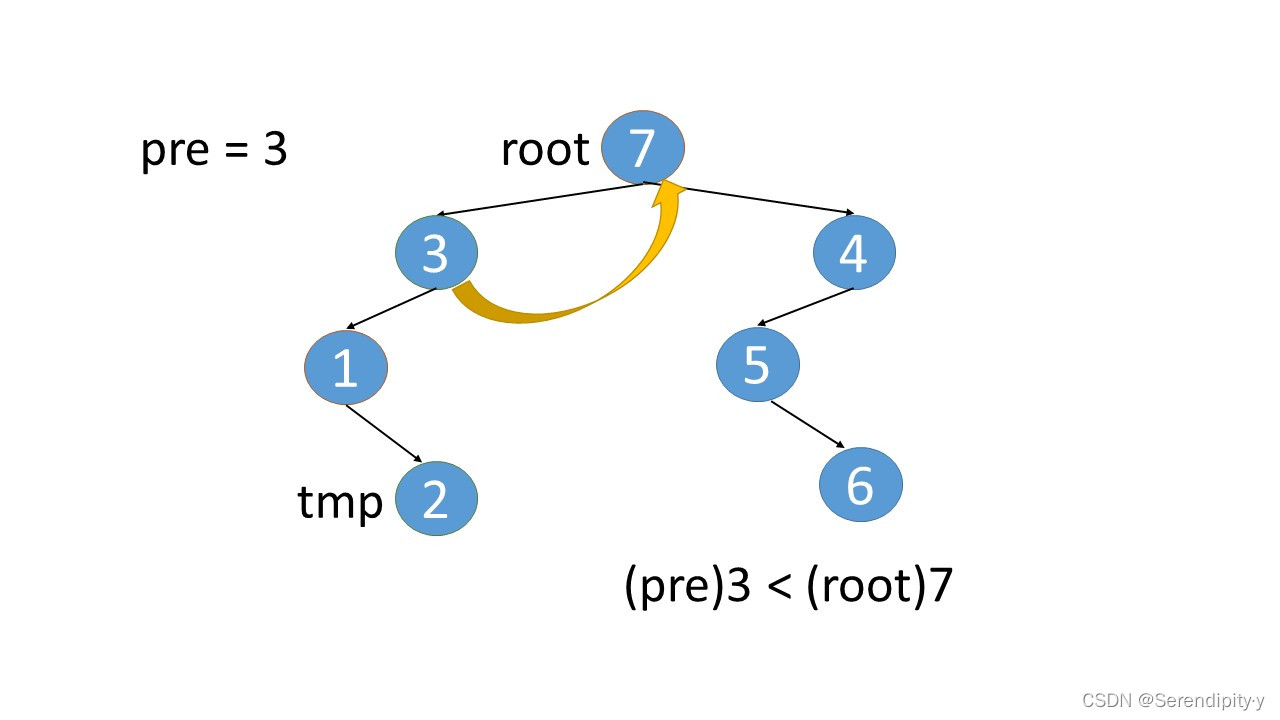
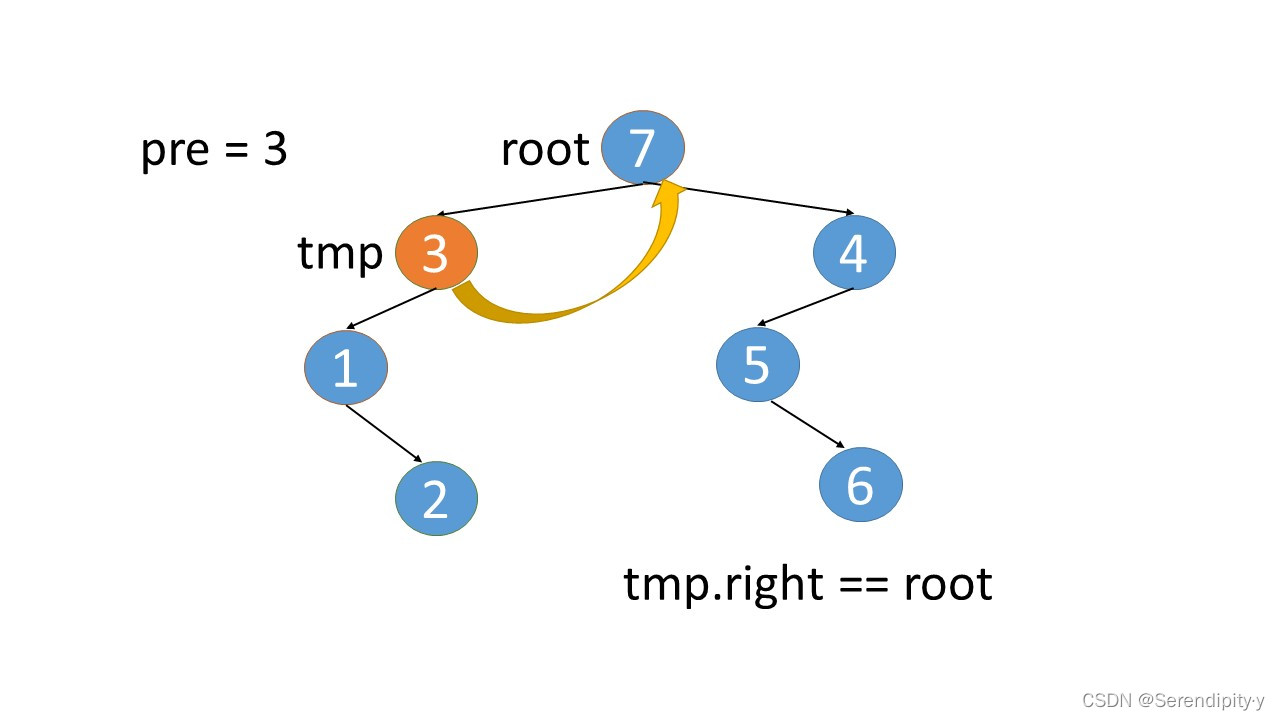
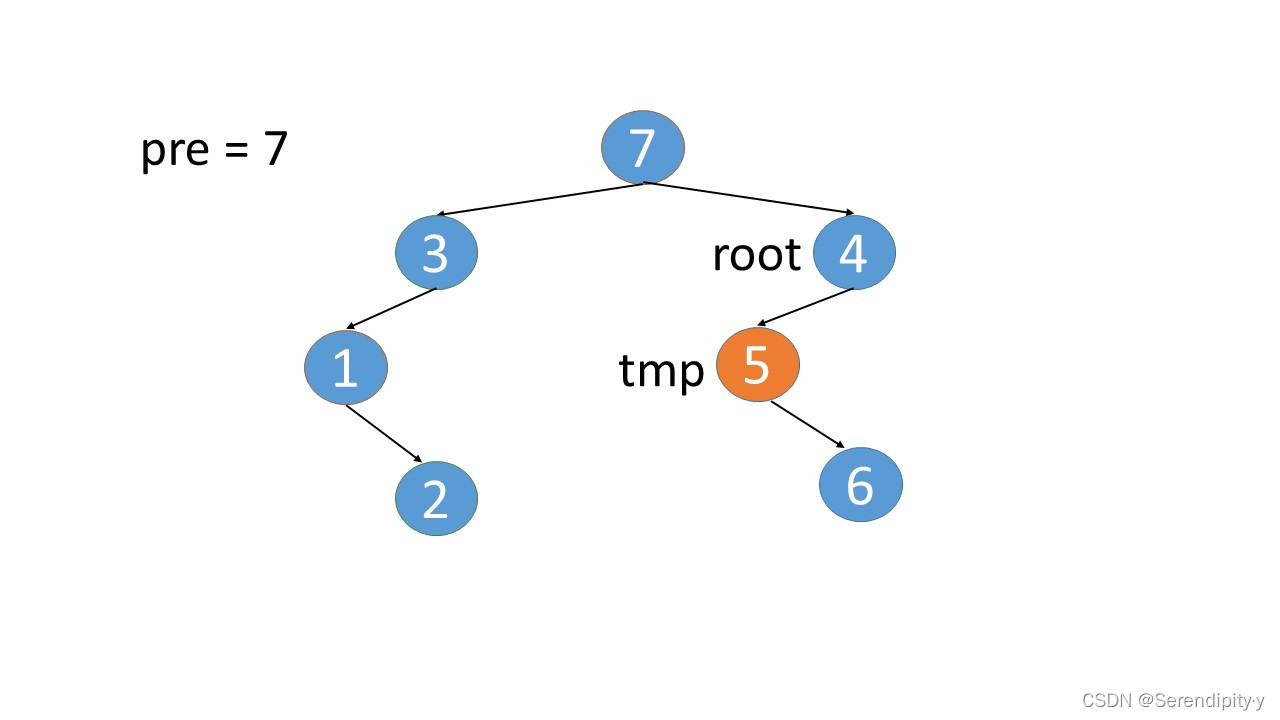
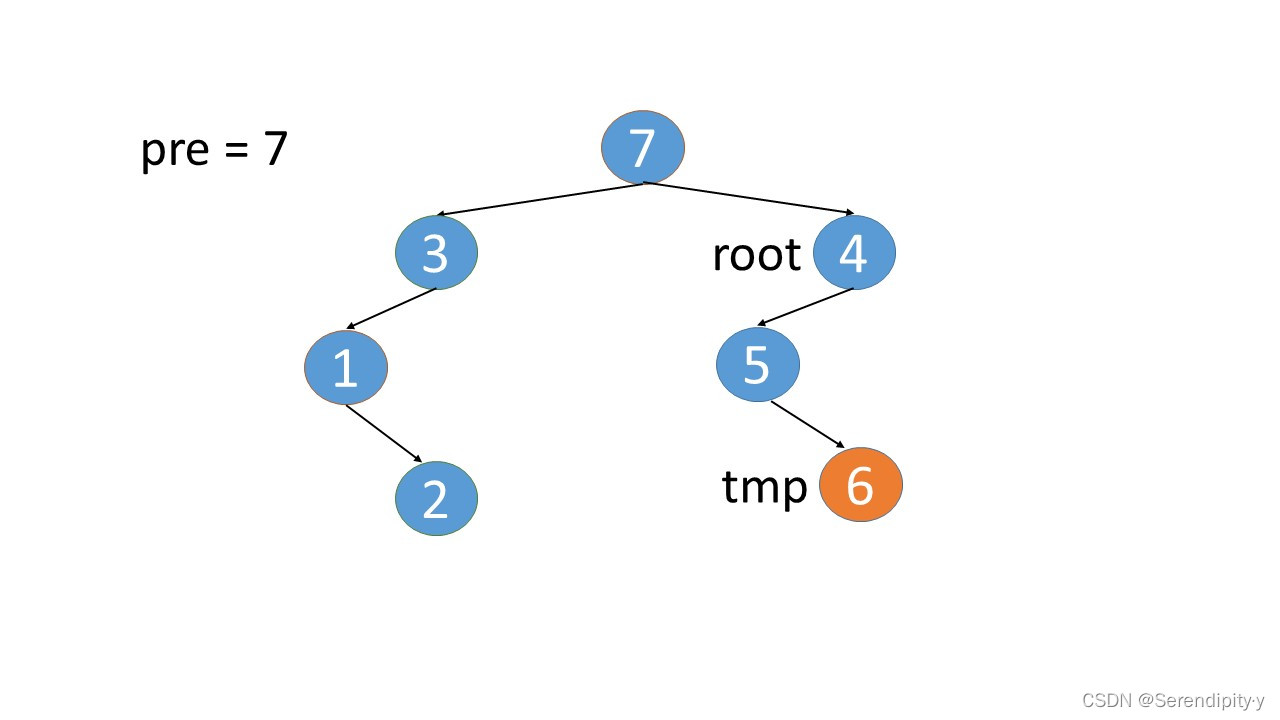
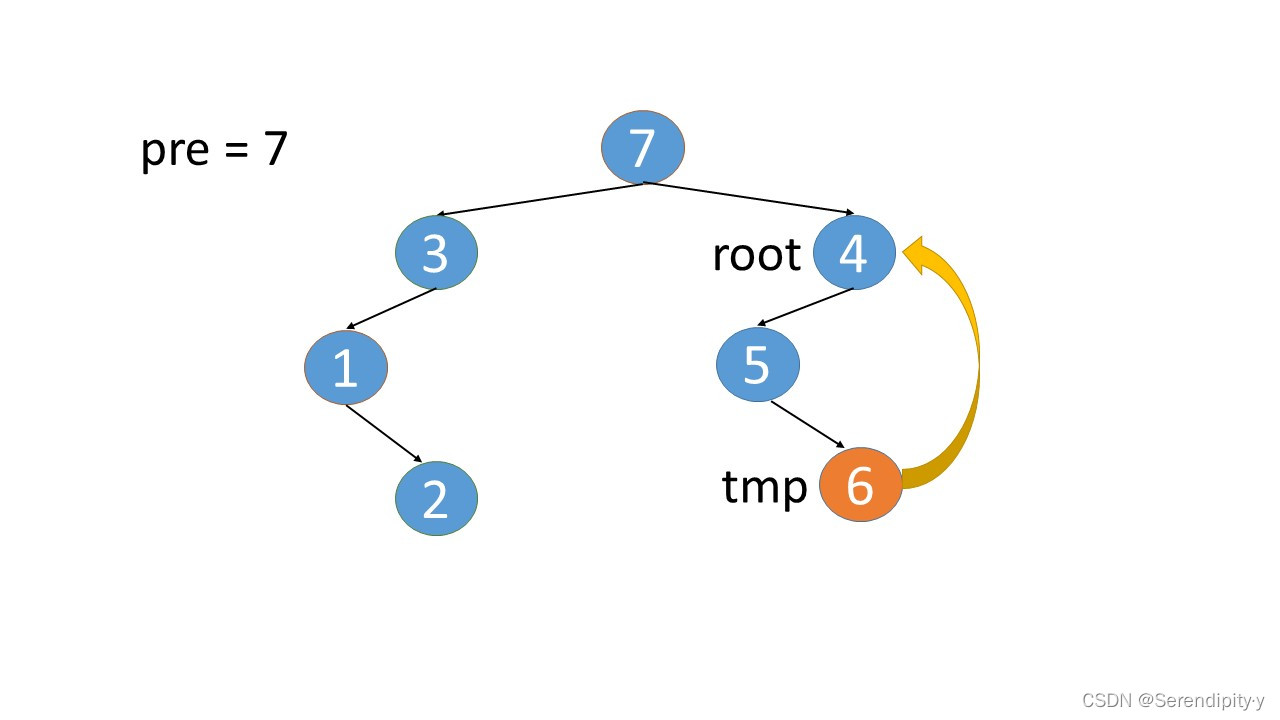
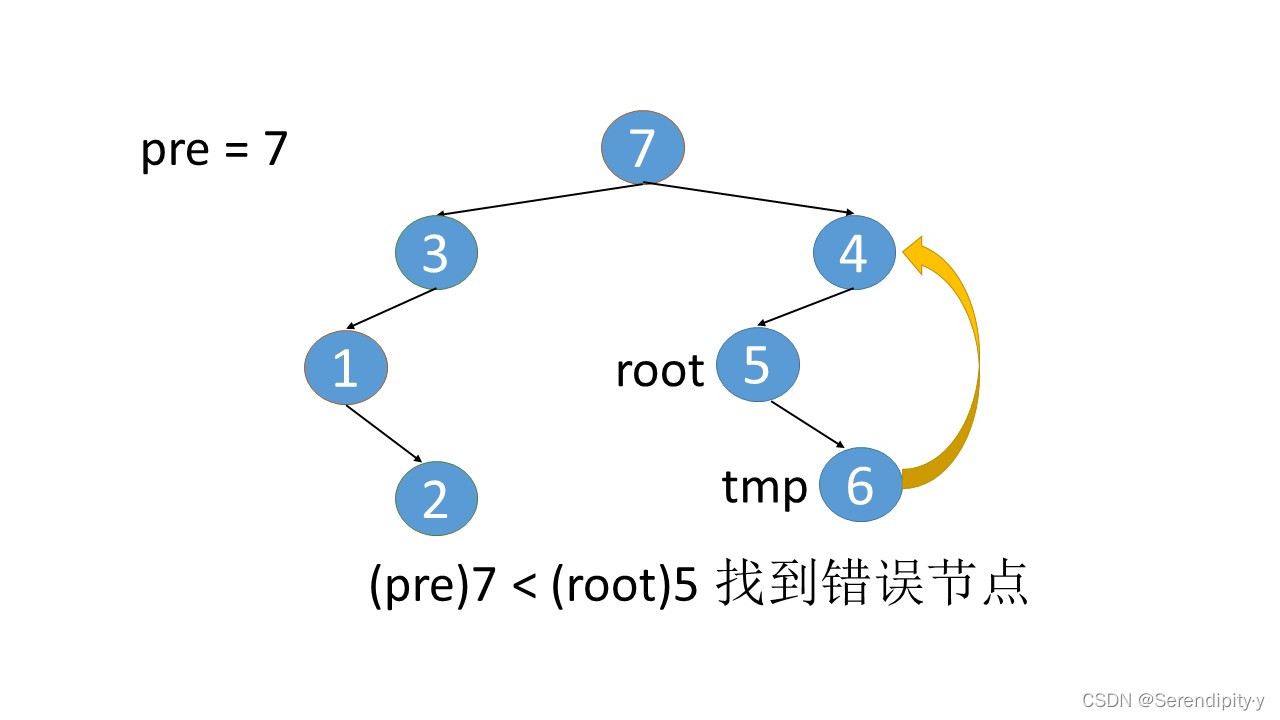
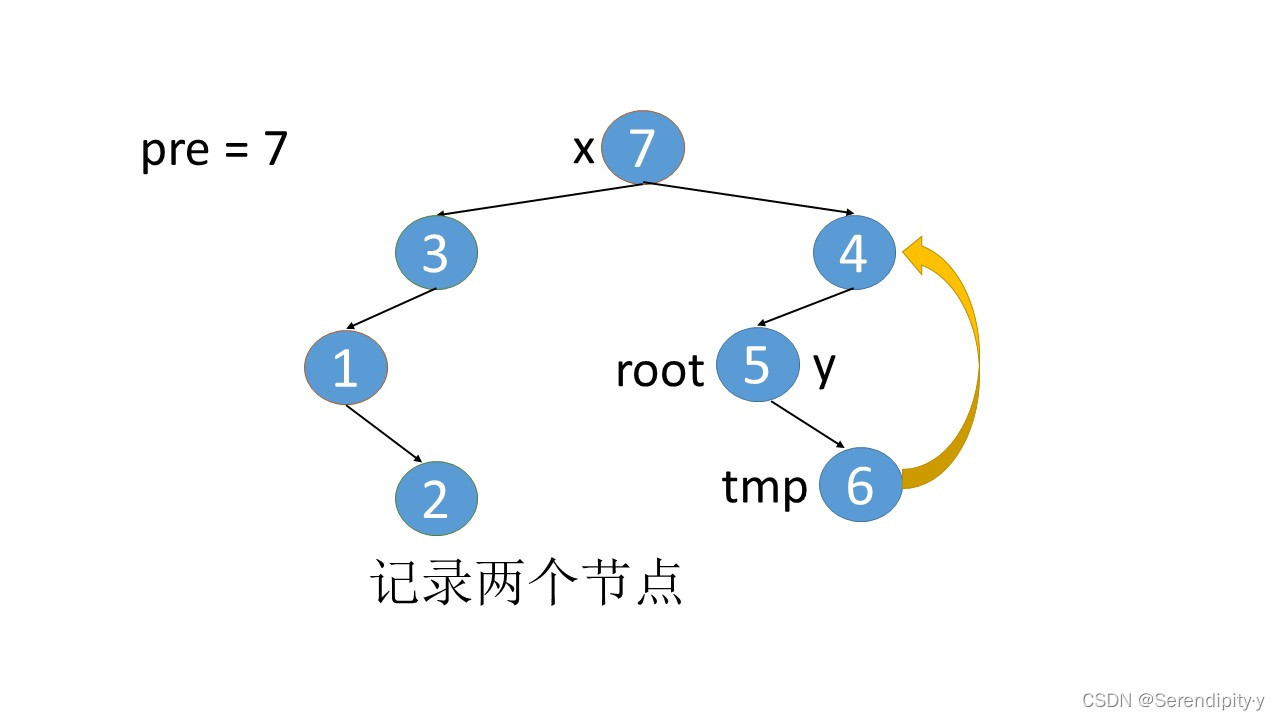
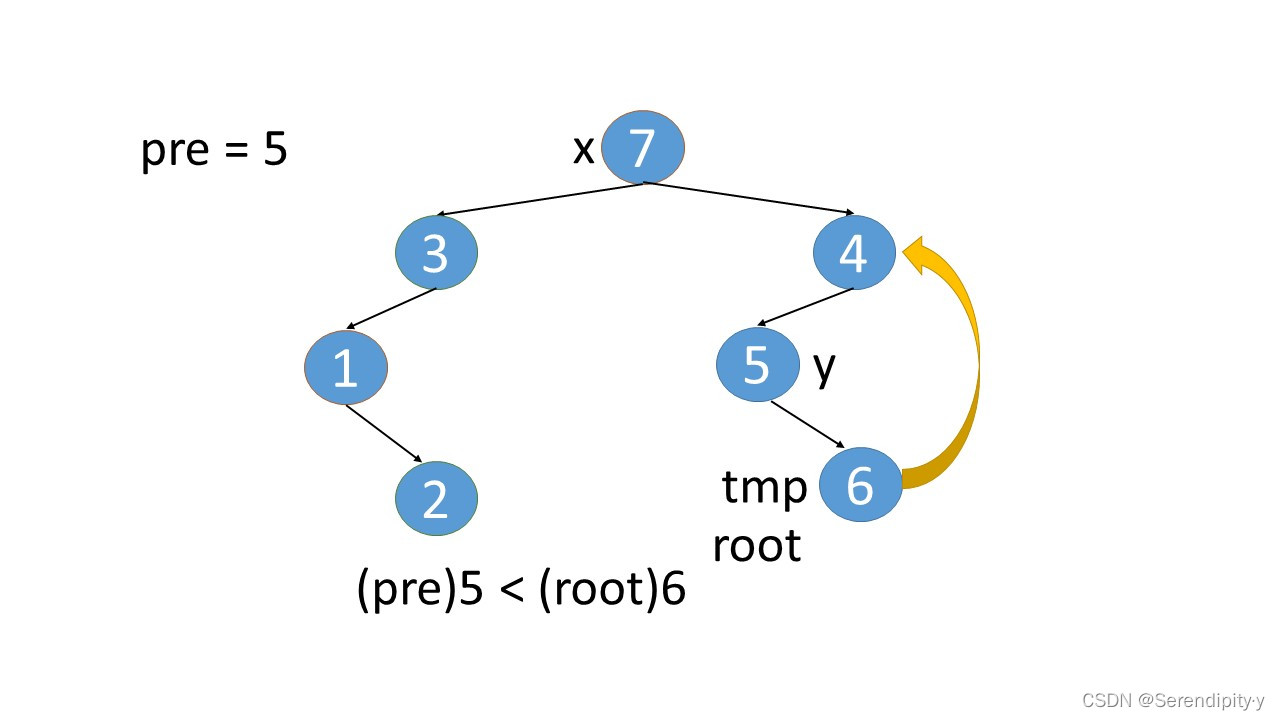
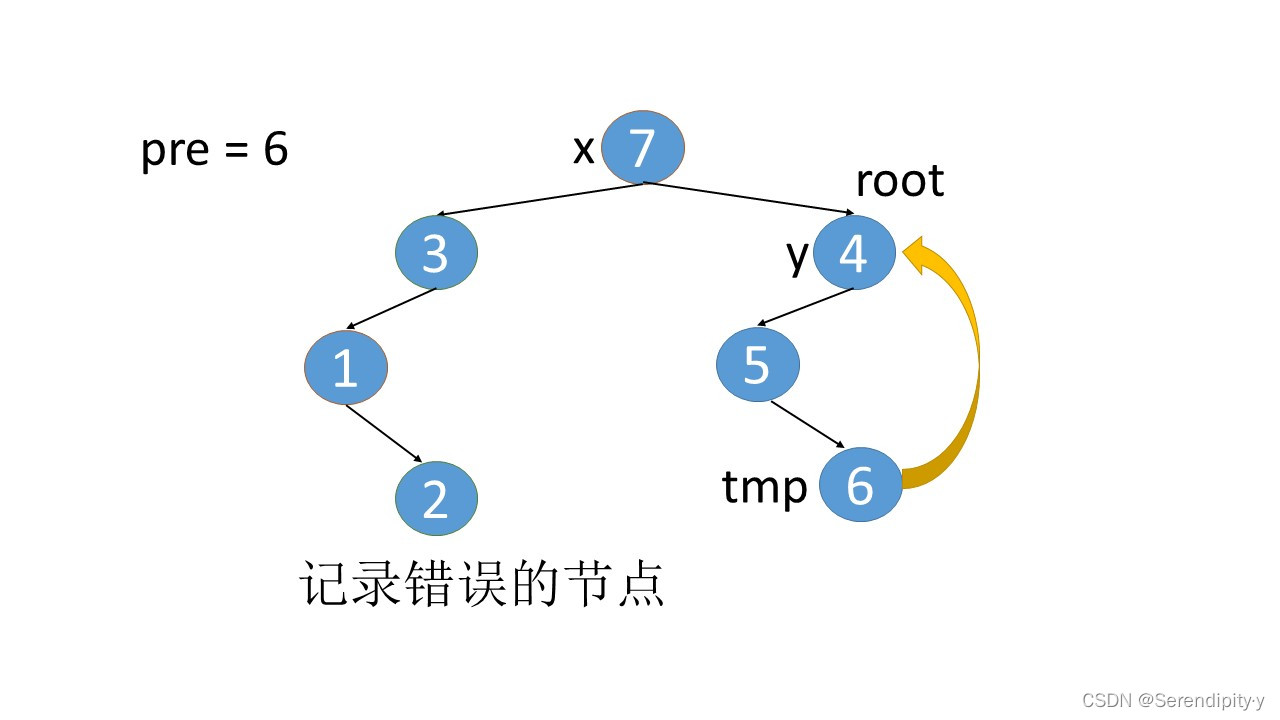
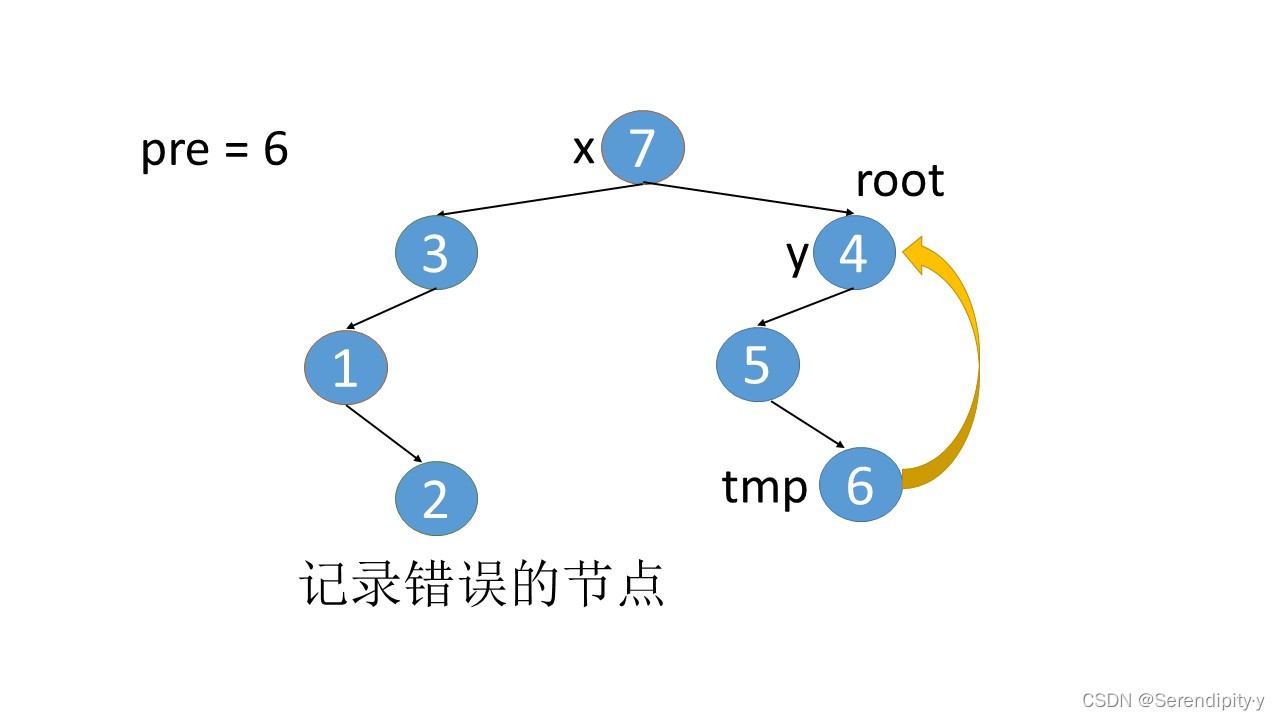
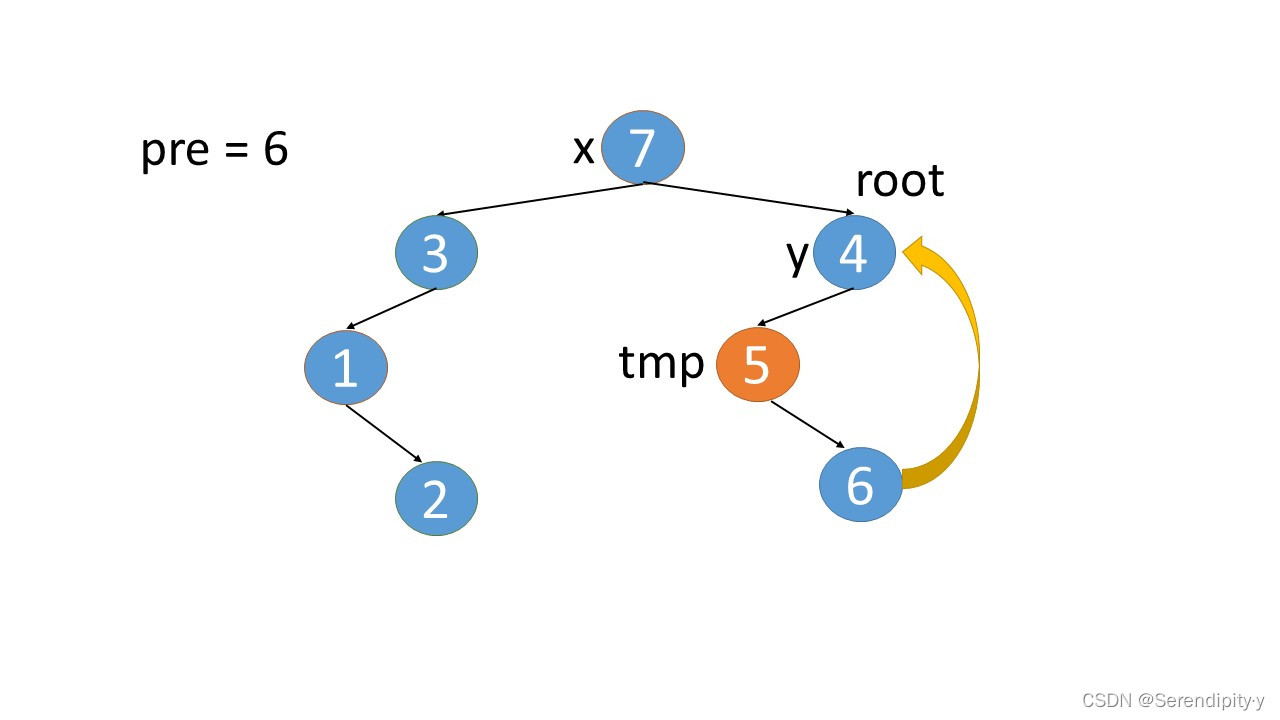
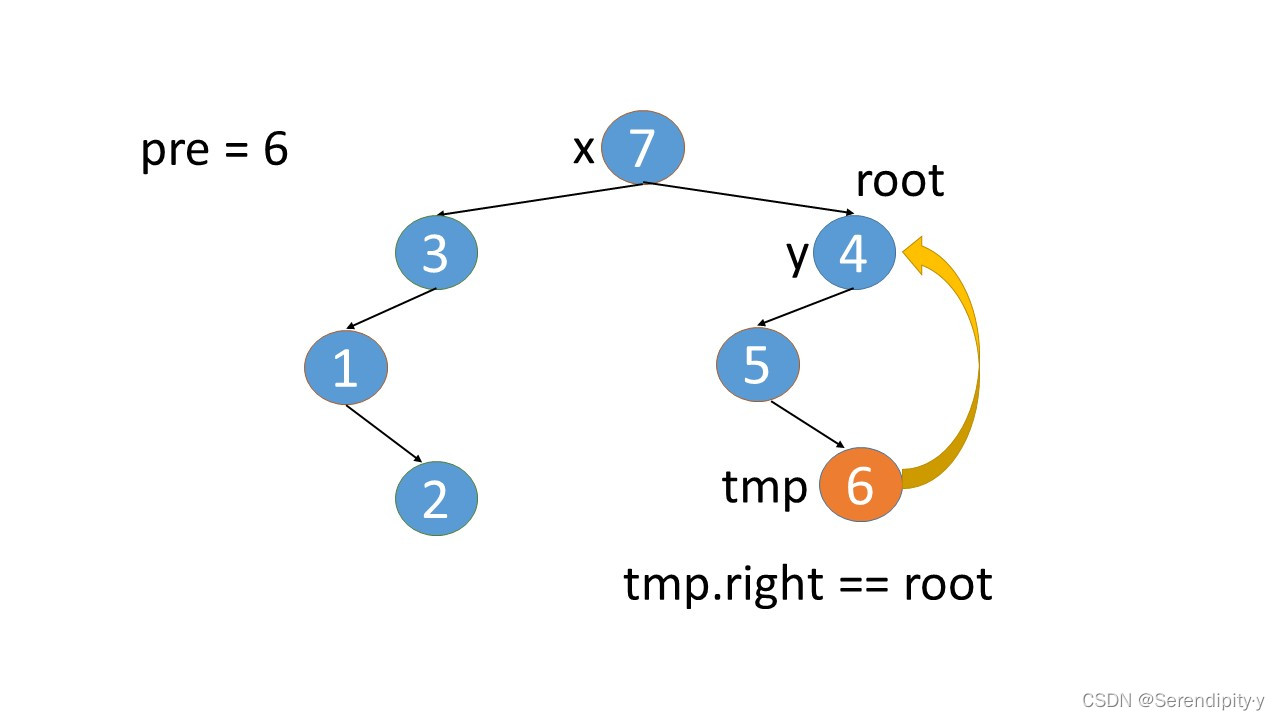
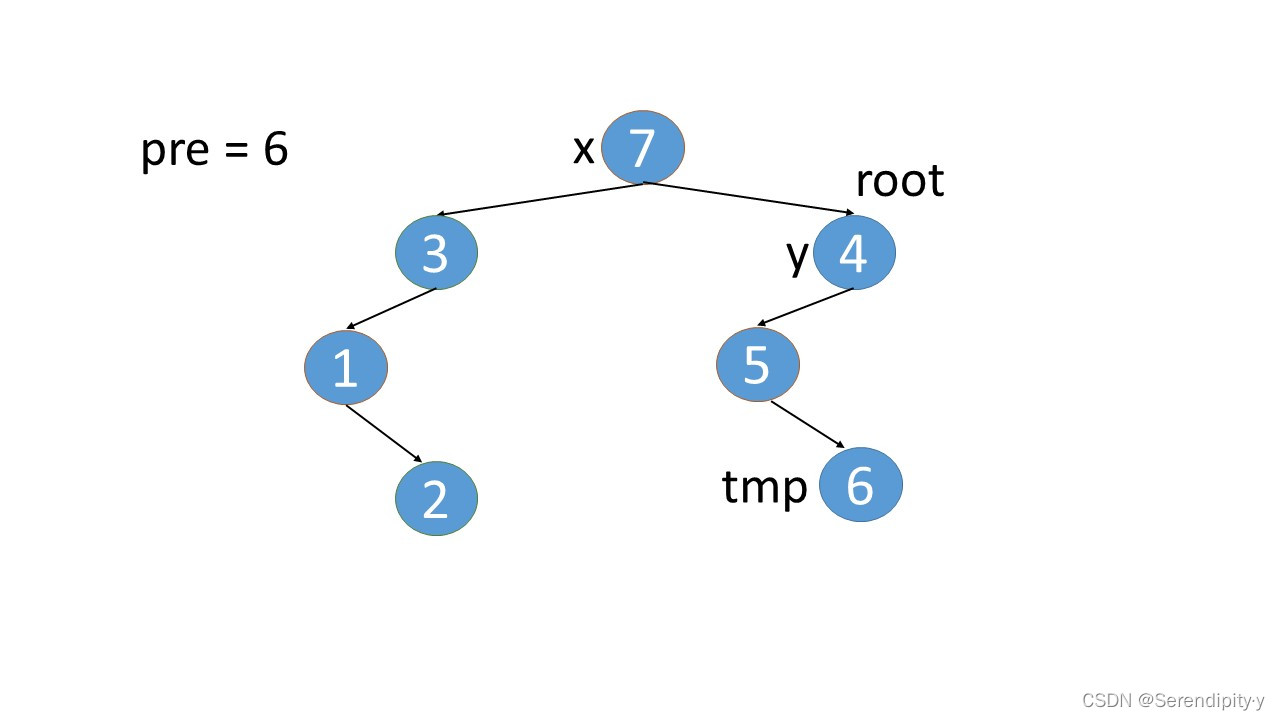
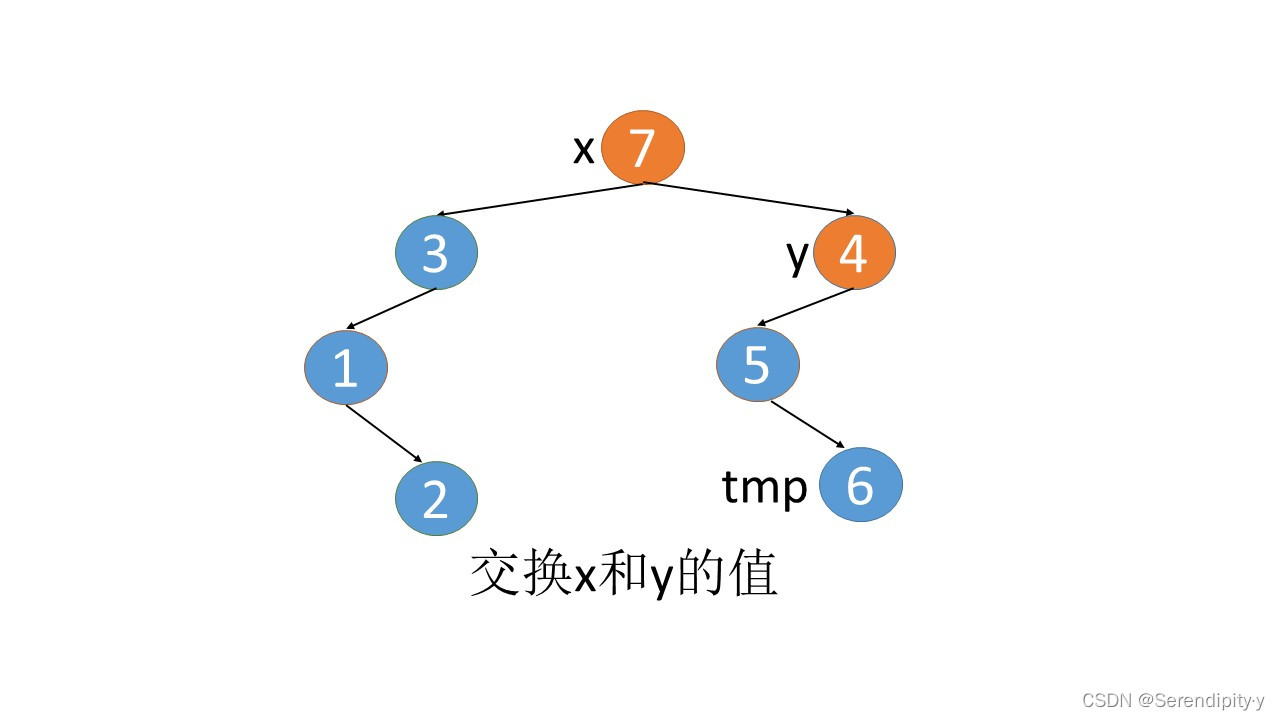
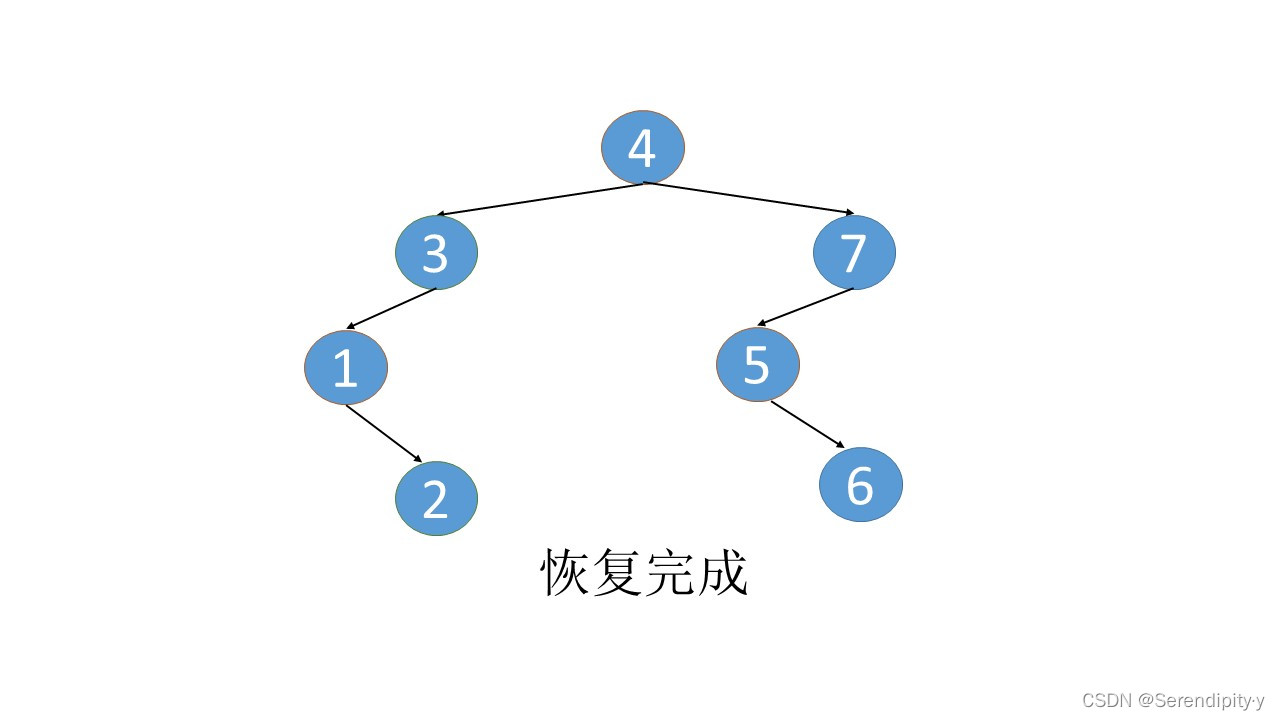
- 看完整个过程,3->1->2,这几个节点会走两遍:第一遍的时候,3 的左子树的最右节点是 2,于是将 2.right 指向 3;之后等 1,2 两个节点都遍历完后,当前节点走到了 3,又会触发一遍 根节点的左子树的最右节点这个循环查找逻辑,此时可以判断出最右的节点 2.right 是等于 root 的,所以就将 2.right 重新设置为空,即还原回去。
- Java 示例:
class Solution {
public void recoverTree(TreeNode root) {
if(root==null) {
return;
}
TreeNode x = null;
TreeNode y = null;
TreeNode pre = null;
TreeNode tmp = null;
while(root!=null) {
if(root.left!=null) {
tmp = root.left;
while(tmp.right!=null && tmp.right!=root) {
tmp = tmp.right;
}
if(tmp.right==null) {
tmp.right = root;
root = root.left;
}
else {
if(pre!=null && pre.val>root.val) {
y = root;
if(x==null) {
x = pre;
}
}
pre = root;
tmp.right = null;
root = root.right;
}
}
else {
if(pre!=null && pre.val>root.val) {
y = root;
if(x==null) {
x = pre;
}
}
pre = root;
root = root.right;
}
}
if(x!=null && y!=null) {
int t = x.val;
x.val = y.val;
y.val = t;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- Python 示例:
class Solution(object):
def recoverTree(self, root):
x = None
y = None
pre = None
tmp = None
while root:
if root.left:
tmp = root.left
while tmp.right and tmp.right!=root:
tmp = tmp.right
if tmp.right is None:
tmp.right = root
root = root.left
else:
if pre and pre.val>root.val:
y = root
if not x:
x = pre
pre = root
tmp.right = None
root = root.right
else:
if pre and pre.val>root.val:
y = root
if not x:
x = pre
pre = root
root = root.right
if x and y:
x.val,y.val = y.val,x.val
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122963015
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)