【数据结构与算法】之深入解析“解数独”的求解思路与算法示例
【摘要】
一、题目要求
编写一个程序,通过填充空格来解决数独问题。数独的解法需遵循如下规则:
数字 1-9 在每一行只能出现一次;
数字 1-9 在每一列只能出现一次;
数字 1-9 在每一...
一、题目要求
- 编写一个程序,通过填充空格来解决数独问题。
- 数独的解法需遵循如下规则:
-
- 数字 1-9 在每一行只能出现一次;
-
- 数字 1-9 在每一列只能出现一次;
-
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次;
-
- 数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
- 示例:

输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
- 1
- 2
- 输入的数独如上图所示,唯一有效的解决方案如下所示:

- 提示:
-
- board.length == 9;
-
- board[i].length == 9;
-
- board[i][j] 是一位数字或者 ‘.’;
-
- 题目数据 保证 输入数独仅有一个解。
二、思路分析
- 可以考虑按照「行优先」的顺序依次枚举每一个空白格中填的数字,通过递归 + 回溯的方法枚举所有可能的填法。当递归到最后一个空白格后,如果仍然没有冲突,说明我们找到了答案;在递归的过程中,如果当前的空白格不能填下任何一个数字,那么就进行回溯。
- 由于每个数字在同一行、同一列、同一个九宫格中只会出现一次,因此我们可以使用 line[i],column[j],block[x][y] 分别表示第 i 行,第 j 列,第 (x,y) 个九宫格中填写数字的情况。在下面给出的三种方法中,将会介绍两种不同的表示填写数字情况的方法。
九宫格的范围为 0≤x≤2 以及 0≤y≤2。具体地,第 i 行第 j 列的格子位于第 (⌊i/3⌋,⌊j/3⌋) 个九宫格中,其中 ⌊u⌋ 表示对
u 向下取整。
- 1
- 2
- 由于这些方法均以递归 + 回溯为基础,算法运行的时间(以及时间复杂度)很大程度取决于给定的输入数据,而我们很难找到一个非常精确的渐进紧界。因此这里只给出一个较为宽松的渐进复杂度上界 O(99×9),即最多有 9×9 个空白格,每个格子可以填 [1,9] 中的任意整数。
三、求解算法
① 递归
- 最容易想到的方法是用一个数组记录每个数字是否出现。由于我们可以填写的数字范围为 [1,9],而数组的下标从 0 开始,因此在存储时,我们使用一个长度为 9 的布尔类型的数组,其中 i 个元素的值为 True,当且仅当数字 i+1 出现过。例如用 line[2][3]=True 表示数字 4 在第 2 行已经出现过,那么当我们在遍历到第 2 行的空白格时,就不能填入数字 4。
- 首先对整个数独数组进行遍历,当遍历到第 i 行第 j 列的位置:
-
- 如果该位置是一个空白格,那么我们将其加入一个用来存储空白格位置的列表中,方便后续的递归操作;
-
- 如果该位置是一个数字 x,那么需要将 line[i][x−1],column[j][x−1] 以及 block[⌊i/3⌋][⌊j/3⌋][x−1] 均置为 True。
- 当结束了遍历过程之后,就可以开始递归枚举。当递归到第 i 行第 j 列的位置时,我们枚举填入的数字 x。根据题目的要求,数字 x 不能和当前行、列、九宫格中已经填入的数字相同,因此 line[i][x−1],column[j][x−1] 以及 block[⌊i/3⌋][⌊j/3⌋][x−1] 必须均为 False。
- 当填入了数字 x 之后,我们要将上述的三个值都置为 True,并且继续对下一个空白格位置进行递归。在回溯到当前递归层时,我们还要将上述的三个值重新置为 False。
- C++ 示例:
class Solution {
private:
bool line[9][9];
bool column[9][9];
bool block[3][3][9];
bool valid;
vector<pair<int, int>> spaces;
public:
void dfs(vector<vector<char>>& board, int pos) {
if (pos == spaces.size()) {
valid = true;
return;
}
auto [i, j] = spaces[pos];
for (int digit = 0; digit < 9 && !valid; ++digit) {
if (!line[i][digit] && !column[j][digit] && !block[i / 3][j / 3][digit]) {
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
board[i][j] = digit + '0' + 1;
dfs(board, pos + 1);
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = false;
}
}
}
void solveSudoku(vector<vector<char>>& board) {
memset(line, false, sizeof(line));
memset(column, false, sizeof(column));
memset(block, false, sizeof(block));
valid = false;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.emplace_back(i, j);
}
else {
int digit = board[i][j] - '0' - 1;
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
}
}
}
dfs(board, 0);
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- Java 示例:
class Solution {
private boolean[][] line = new boolean[9][9];
private boolean[][] column = new boolean[9][9];
private boolean[][][] block = new boolean[3][3][9];
private boolean valid = false;
private List<int[]> spaces = new ArrayList<int[]>();
public void solveSudoku(char[][] board) {
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
} else {
int digit = board[i][j] - '0' - 1;
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
}
}
}
dfs(board, 0);
}
public void dfs(char[][] board, int pos) {
if (pos == spaces.size()) {
valid = true;
return;
}
int[] space = spaces.get(pos);
int i = space[0], j = space[1];
for (int digit = 0; digit < 9 && !valid; ++digit) {
if (!line[i][digit] && !column[j][digit] && !block[i / 3][j / 3][digit]) {
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
board[i][j] = (char) (digit + '0' + 1);
dfs(board, pos + 1);
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = false;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
② 位运算优化
- 在方法①中,我们使用了长度为 9 的数组表示每个数字是否出现过,同样也可以借助位运算,仅使用一个整数表示每个数字是否出现过。
- 具体地,数 b 的二进制表示的第 i 位(从低到高,最低位为第 0 位)为 1,当且仅当数字 i+1 已经出现过。例如当 b 的二进制表示为 (011000100)2 时,就表示数字 3,7,8 已经出现过。
- 位运算有一些基础的使用技巧,下面列举了所有在代码中使用到的技巧:
-
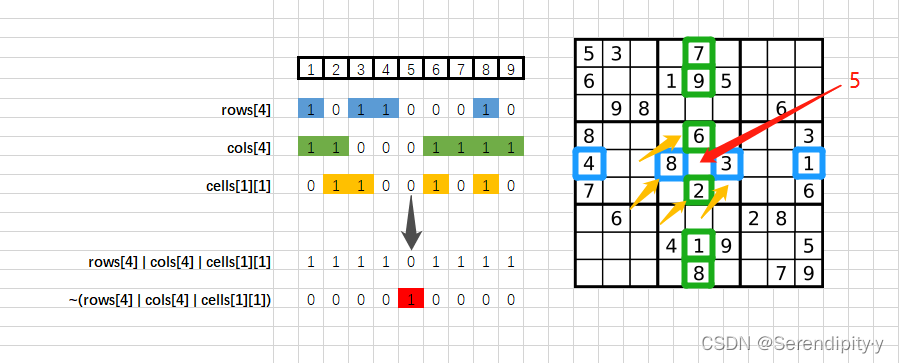
- 对于第 i 行第 j 列的位置,line[i] ∣ column[j] ∣ block[⌊i/3⌋][⌊j/3⌋] 中第 k 位为 1,表示该位置不能填入数字 k+1(因为已经出现过),其中 ∣ 表示按位或运算。如果我们对这个值进行 ∼ 按位取反运算,那么第 k 位为 1 就表示该位置可以填入数字 k+1,我们就可以通过寻找 1 来进行枚举。由于在进行按位取反运算后,这个数的高位也全部变成了 1,而这是我们不应当枚举到的,因此需要将这个数和 (111111111)2 =(1FF) 16 进行按位与运算 &,将所有无关的位置为 0;
-
- 可以使用按位异或运算 ∧,将第 i 位从 0 变为 1,或从 1 变为 0。具体地,与数 1<<i 进行按位异或运算即可,其中 << 表示左移运算;
-
- 可以用 b & (−b) 得到 b 二进制表示中最低位的 1,这是因为 (−b) 在计算机中以补码的形式存储,它等于 ∼b+1。b 如果和 ∼b 进行按位与运算,那么会得到 0,但是当 ∼b 增加 1 之后,最低位的连续的 1 都变为 0,而最低位的 0 变为 1,对应到 b 中即为最低位的 1,因此当 b 和 ∼b+1 进行按位与运算时,只有最低位的 1 会被保留;
-
- 当得到这个最低位的 1 时,我们可以通过一些语言自带的函数得到这个最低位的 1 究竟是第几位(即 i 值),具体可以参考下面的代码;
-
- 可以用 b 和最低位的 1 进行按位异或运算,就可以将其从 b 中去除,这样就可以枚举下一个 1。同样地,我们也可以用 b 和 b−1 进行按位与运算达到相同的效果,读者可以自行尝试推导。
- C++ 示例:
class Solution {
private:
int line[9];
int column[9];
int block[3][3];
bool valid;
vector<pair<int, int>> spaces;
public:
void flip(int i, int j, int digit) {
line[i] ^= (1 << digit);
column[j] ^= (1 << digit);
block[i / 3][j / 3] ^= (1 << digit);
}
void dfs(vector<vector<char>>& board, int pos) {
if (pos == spaces.size()) {
valid = true;
return;
}
auto [i, j] = spaces[pos];
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
for (; mask && !valid; mask &= (mask - 1)) {
int digitMask = mask & (-mask);
int digit = __builtin_ctz(digitMask);
flip(i, j, digit);
board[i][j] = digit + '0' + 1;
dfs(board, pos + 1);
flip(i, j, digit);
}
}
void solveSudoku(vector<vector<char>>& board) {
memset(line, 0, sizeof(line));
memset(column, 0, sizeof(column));
memset(block, 0, sizeof(block));
valid = false;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.emplace_back(i, j);
}
else {
int digit = board[i][j] - '0' - 1;
flip(i, j, digit);
}
}
}
dfs(board, 0);
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- Java 示例:
class Solution {
private int[] line = new int[9];
private int[] column = new int[9];
private int[][] block = new int[3][3];
private boolean valid = false;
private List<int[]> spaces = new ArrayList<int[]>();
public void solveSudoku(char[][] board) {
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
} else {
int digit = board[i][j] - '0' - 1;
flip(i, j, digit);
}
}
}
dfs(board, 0);
}
public void dfs(char[][] board, int pos) {
if (pos == spaces.size()) {
valid = true;
return;
}
int[] space = spaces.get(pos);
int i = space[0], j = space[1];
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
for (; mask != 0 && !valid; mask &= (mask - 1)) {
int digitMask = mask & (-mask);
int digit = Integer.bitCount(digitMask - 1);
flip(i, j, digit);
board[i][j] = (char) (digit + '0' + 1);
dfs(board, pos + 1);
flip(i, j, digit);
}
}
public void flip(int i, int j, int digit) {
line[i] ^= (1 << digit);
column[j] ^= (1 << digit);
block[i / 3][j / 3] ^= (1 << digit);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
③ 回溯 + 状态压缩
- 状态压缩:
-
- 使用 bitset<9> 来压缩存储每一行、每一列、每一个 3x3 宫格中 1-9 是否出现;
-
- 这样每一个格子就可以计算出所有不能填的数字,然后得到所有能填的数字 getPossibleStatus();
-
- 填入数字和回溯时,只需要更新存储信息;
-
- 每个格子在使用时,会根据存储信息重新计算能填的数字。
- 回溯:
-
- 每次都使用 getNext() 选择能填的数字最少的格子开始填,这样填错的概率最小,回溯次数也会变少;
-
- 使用 fillNum() 在填入和回溯时负责更新存储信息;
-
- 一旦全部填写成功,一路返回 true ,结束递归。
- C++ 示例:
class Solution {
public:
bitset<9> getPossibleStatus(int x, int y)
{
return ~(rows[x] | cols[y] | cells[x / 3][y / 3]);
}
vector<int> getNext(vector<vector<char>>& board)
{
vector<int> ret;
int minCnt = 10;
for (int i = 0; i < board.size(); i++)
{
for (int j = 0; j < board[i].size(); j++)
{
if (board[i][j] != '.') continue;
auto cur = getPossibleStatus(i, j);
if (cur.count() >= minCnt) continue;
ret = { i, j };
minCnt = cur.count();
}
}
return ret;
}
void fillNum(int x, int y, int n, bool fillFlag)
{
rows[x][n] = (fillFlag) ? 1 : 0;
cols[y][n] = (fillFlag) ? 1 : 0;
cells[x/3][y/3][n] = (fillFlag) ? 1: 0;
}
bool dfs(vector<vector<char>>& board, int cnt)
{
if (cnt == 0) return true;
auto next = getNext(board);
auto bits = getPossibleStatus(next[0], next[1]);
for (int n = 0; n < bits.size(); n++)
{
if (!bits.test(n)) continue;
fillNum(next[0], next[1], n, true);
board[next[0]][next[1]] = n + '1';
if (dfs(board, cnt - 1)) return true;
board[next[0]][next[1]] = '.';
fillNum(next[0], next[1], n, false);
}
return false;
}
void solveSudoku(vector<vector<char>>& board)
{
rows = vector<bitset<9>>(9, bitset<9>());
cols = vector<bitset<9>>(9, bitset<9>());
cells = vector<vector<bitset<9>>>(3, vector<bitset<9>>(3, bitset<9>()));
int cnt = 0;
for (int i = 0; i < board.size(); i++)
{
for (int j = 0; j < board[i].size(); j++)
{
cnt += (board[i][j] == '.');
if (board[i][j] == '.') continue;
int n = board[i][j] - '1';
rows[i] |= (1 << n);
cols[j] |= (1 << n);
cells[i / 3][j / 3] |= (1 << n);
}
}
dfs(board, cnt);
}
private:
vector<bitset<9>> rows;
vector<bitset<9>> cols;
vector<vector<bitset<9>>> cells;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122766419
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)