【数据结构与算法】之深入解析“搜索旋转排序数组II”的求解思路与算法示例
【摘要】
一、题目要求
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了...
一、题目要求
- 已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
- 在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了旋转 ,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标从 0 开始计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
- 给你旋转后的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
- 必须尽可能减少整个操作步骤。
- 示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
- 1
- 2
- 示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
- 1
- 2
- 提示:
-
- 1 <= nums.length <= 5000;
-
- 104 <= nums[i] <= 104;
-
- 题目数据保证 nums 在预先未知的某个下标上进行了旋转;
-
- -104 <= target <= 104。
- 进阶:
-
- 这是【数据结构与算法】之深入解析“搜索旋转排序数组”的求解思路与算法示例 的延伸题目,本题中的 nums 可能包含重复元素。
-
- 这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
二、求解算法
① 二分查找
- 是【数据结构与算法】之深入解析“搜索旋转排序数组”的求解思路与算法示例 的升级版,搜索旋转排序数组中,整数数组 nums 原本是个升序排列且无重复元素的数组,而在本题搜索旋转排序数组Ⅱ中,整数数组 nums 成了非降序排列且可能出现重复元素的数组,就是在数组从【无重复元素】的数组变成了【可能存在重复元素】的数组。
- 数组被旋转以后,总有一部分还是有序的。没重复元素的时候,比如 [4,5,6,7,0,1,2] 中,找到 mid,不管是 0 ~ mid 或者 mid ~ n-1,总还有部分是有序的。要是 nums[low] <= nums[mid],那就是左区间有序,否则右区间有序。但是现在出现了重复元素以后,这样判断可能会失效,因为可能有 [4,5,4,4,4] 这种情况,此时 nums[low] == nums[mid] == nums[high],这就没法判断左区间和右区间哪个是有序的。
- 碰到这种情况,一般的解决办法就是收缩区间,收缩区间就是 low 向右移动,同时 high 向左移动,直至出现 num[low] != nums[mid] 或者 nums[mid] != nums[high] 的情况。
- 具体步骤:
-
- 找出 mid,如果 nums[mid] == target,直接返回;
-
- 如果 nums[low] == nums[mid] == nums[high],low 向右移动,high 向左移动;
-
- 如果 [low,mid-1] 有序:
-
-
- target 在 [nums[low],nums[mid]] 中,范围缩小至 [low,mid-1];
-
-
-
- target 不在 [nums[low],nums[mid]] 中,范围缩小至 [mid+1,high]。
-
-
- 如果 [mid+1,high] 有序:
-
-
- target 在 [nums[mid+1],nums[high]] 中,范围缩小至 [mid+1,high];
-
-
-
- target 不在 [nums[mid+1],nums[high]] 中,范围缩小至 [low,mid-1]。
-
- 以 nums = [3,1,2,3,3,3,3], target = 2 为例:
-
- 首先初始化 low 和 high 指针:
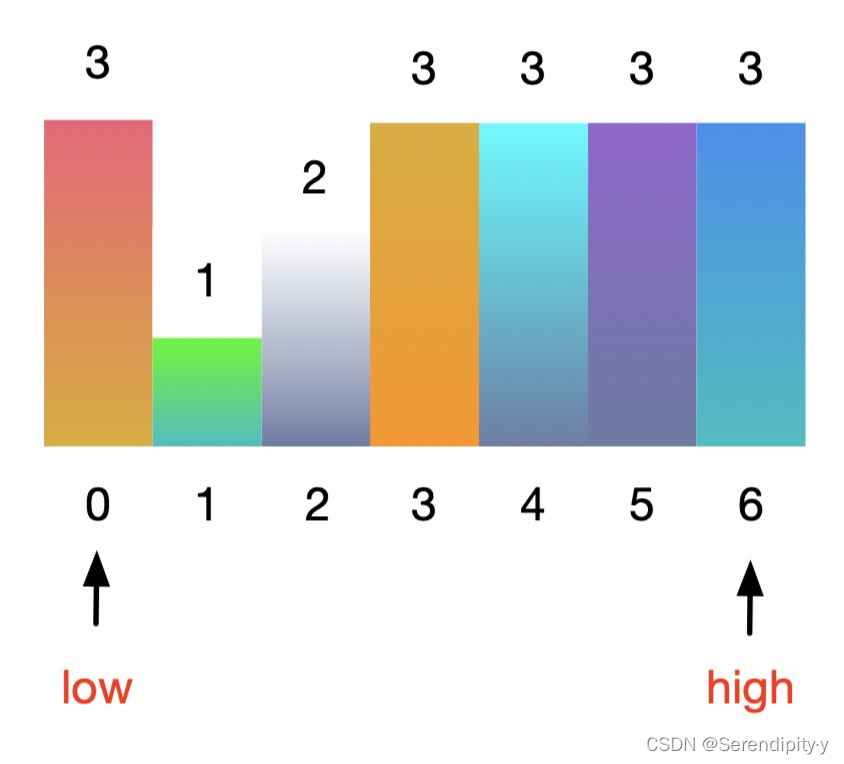
low, high = 0, len(nums) - 1
- 1
-
- 然后,low = 0,high = 6,mid = low + (high - low) // 2 = 3:
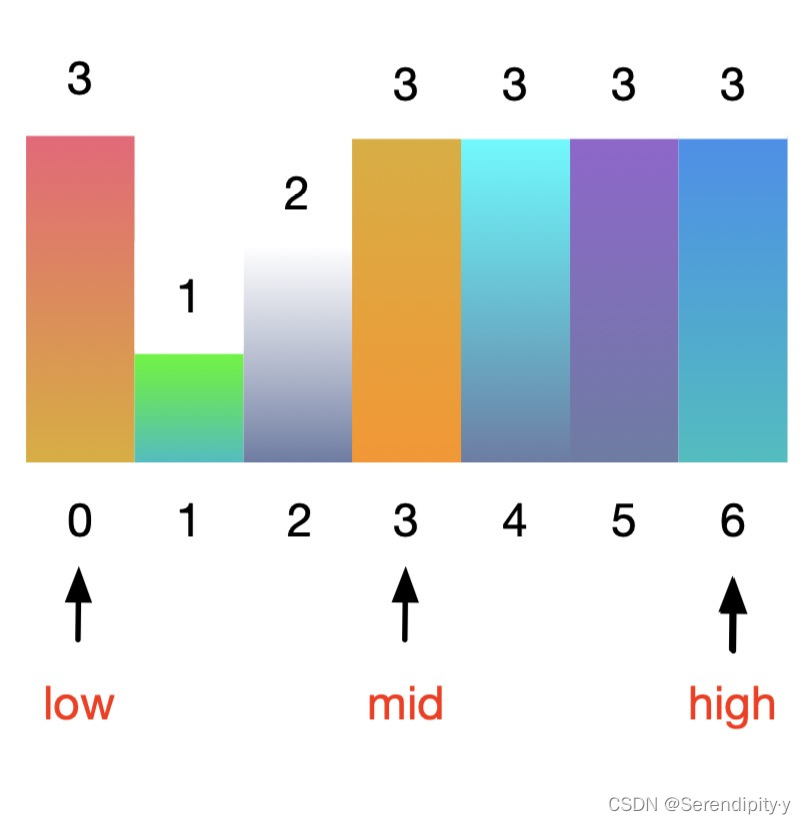
mid = low + (high - low) // 2
- 1
-
- 此时 nums[low] == nums[mid] == nums[high],low 向右移动,high 向左移动:

# 相当于去重
if nums[low] == nums[mid] == nums[high]:
low += 1
high -= 1
- 1
- 2
- 3
- 4
-
- 继续,low = 1,high = 5,mid = low + (high - low) // 2 = 3:

-
- 此时 nums[low] < nums[mid],且 target 在左区间内,所以 high 向左移动至 mid - 1 = 2:
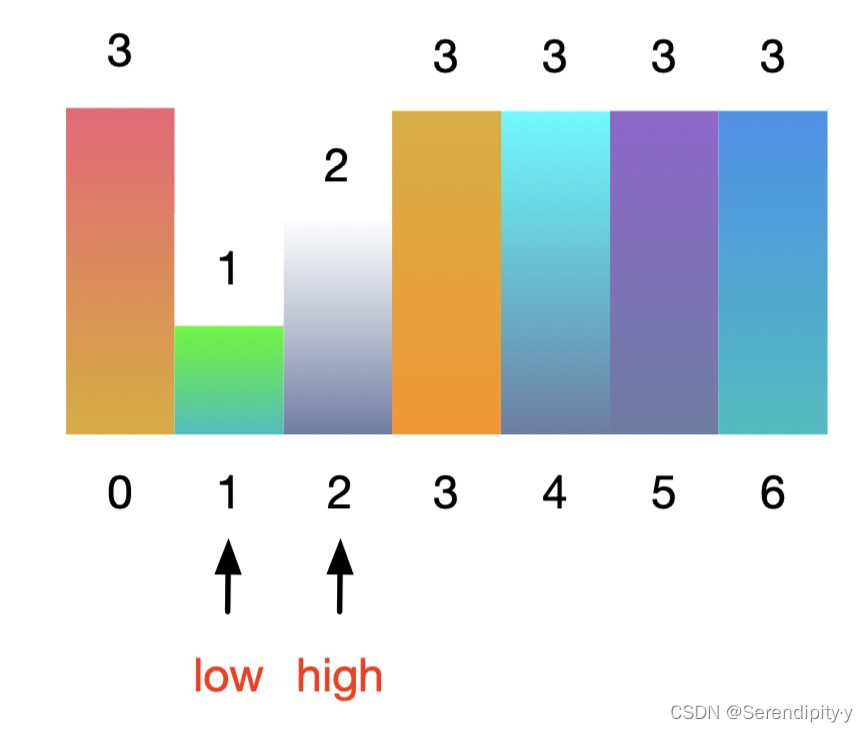
# 如果左区间有序
elif nums[low] <= nums[mid]:
# target 在左区间
if nums[low] <= target < nums[mid]:
high = mid - 1
- 1
- 2
- 3
- 4
- 5
-
- 继续,low = 1,high = 2,mid = low + (high - low) // 2 = 1:
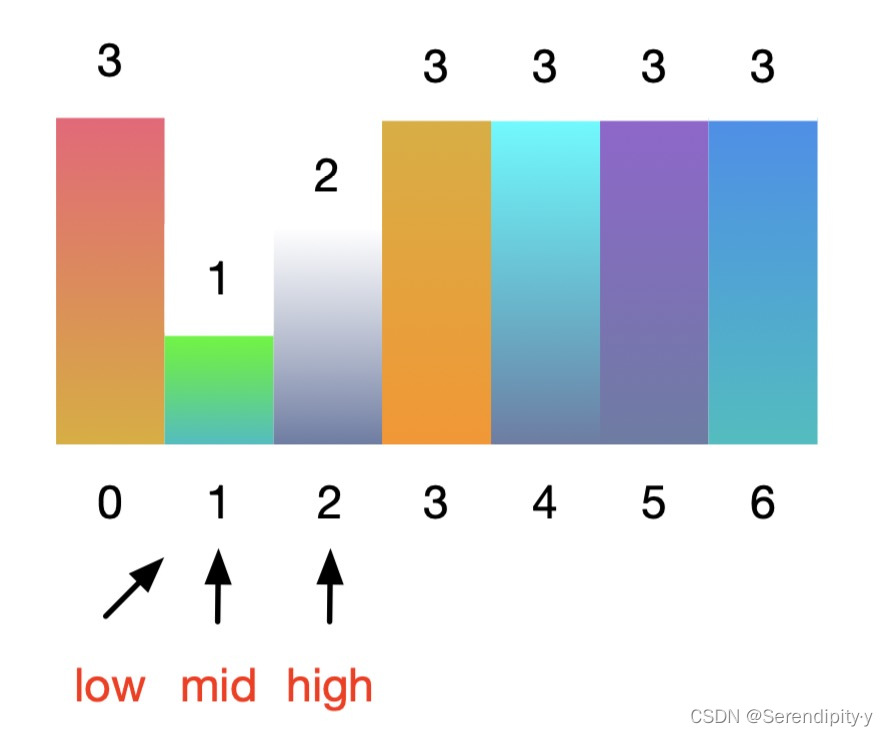
-
- 此时 nums[low] <= nums[mid],且 target 在右区间内,所以 low 向右移动至 mid + 1 = 2:
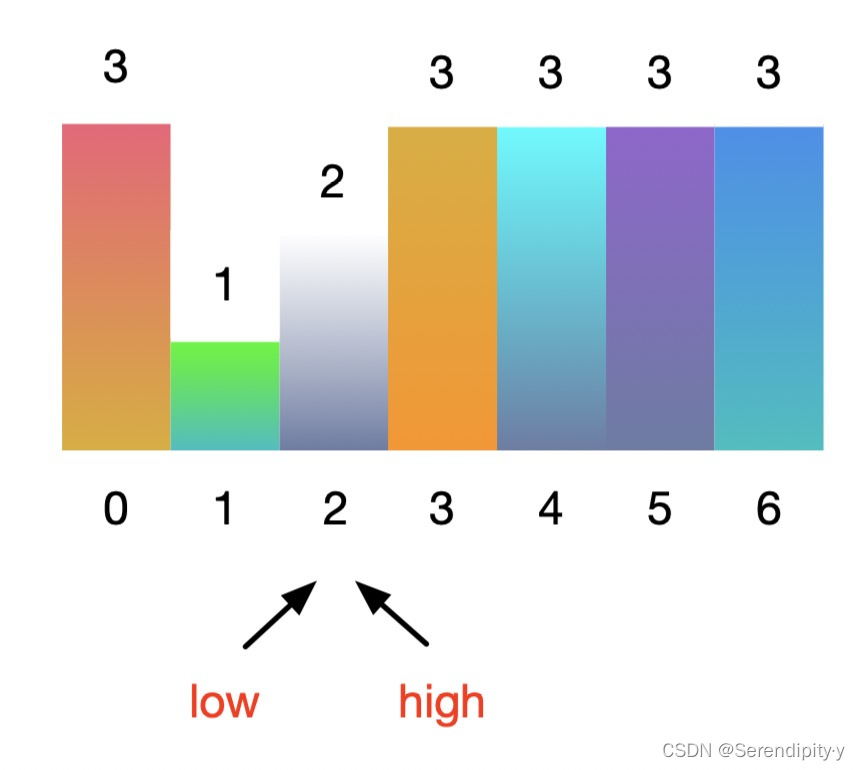
-
- 最后,low = 2,high = 2,mid = low + (high - low) // 2 = 2,此时 nums[mid] == target,直接返回 True。
# 如果找到,返回结果
if nums[mid] == target:
return True
- 1
- 2
- 3
- Java 示例:
class Solution {
public boolean search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return false;
}
if (n == 1) {
return nums[0] == target;
}
int low = 0, high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[low] == nums[mid] && nums[mid] == nums[high]) {
++low;
--high;
} else if (nums[low] <= nums[mid]) {
if (nums[low] <= target && target < nums[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[high]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
}
return false;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- Python 示例:
class Solution:
def search(self, nums: List[int], target: int) -> bool:
if not nums:
return False
low, high = 0, len(nums) - 1
while low <= high:
mid = low + (high - low) // 2
# 如果找到,返回结果
if nums[mid] == target:
return True
# 相当于去重
if nums[low] == nums[mid] == nums[high]:
low += 1
high -= 1
# 如果左区间有序
elif nums[low] <= nums[mid]:
# target 在左区间
if nums[low] <= target < nums[mid]:
high = mid - 1
# target 在右区间
else:
low = mid + 1
# 如果右区间有序
else:
# target 在右区间
if nums[mid] < target <= nums[high]:
low = mid + 1
# target 在左区间
else:
high = mid - 1
return False
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
② 二分查找(LeetCode 官方解法)
- 对于数组中有重复元素的情况,二分查找时可能会有 a[l]=a[mid]=a[r],此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。
- 例如 nums=[3,1,2,3,3,3,3],target=2,首次二分时无法判断区间 [0,3] 和区间 [4,6] 哪个是有序的。对于这种情况,只能将当前二分区间的左边界加一,右边界减一,然后在新区间上继续二分查找。
- Java 示例:
class Solution {
public boolean search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return false;
}
if (n == 1) {
return nums[0] == target;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
} else if (nums[l] <= nums[mid]) {
if (nums[l] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return false;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- C++ 示例:
class Solution {
public:
bool search(vector<int> &nums, int target) {
int n = nums.size();
if (n == 0) {
return false;
}
if (n == 1) {
return nums[0] == target;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
} else if (nums[l] <= nums[mid]) {
if (nums[l] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return false;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122869062
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)