【数据结构与算法】之深入解析“合并区间”的求解思路与算法示例

一、题目要求

• 以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。
• 示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]

  

 

  
1
  
2
  
3
 

• 示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间

  

 

  
1
  
2
  
3
 

• 提示：
• • 1 <= intervals.length <= 104；
• • intervals[i].length == 2；
• • 0 <= starti <= endi <= 104。

二、求解算法

① 排序 + 双指针

• 对 vector<vector> 排序，需要按照先比较区间开始，如果相同再比较区间结束，使用默认的排序规则即可；
• 使用双指针，左边指针指向当前区间的开始；
• 使用一个变量来记录连续的范围 t；

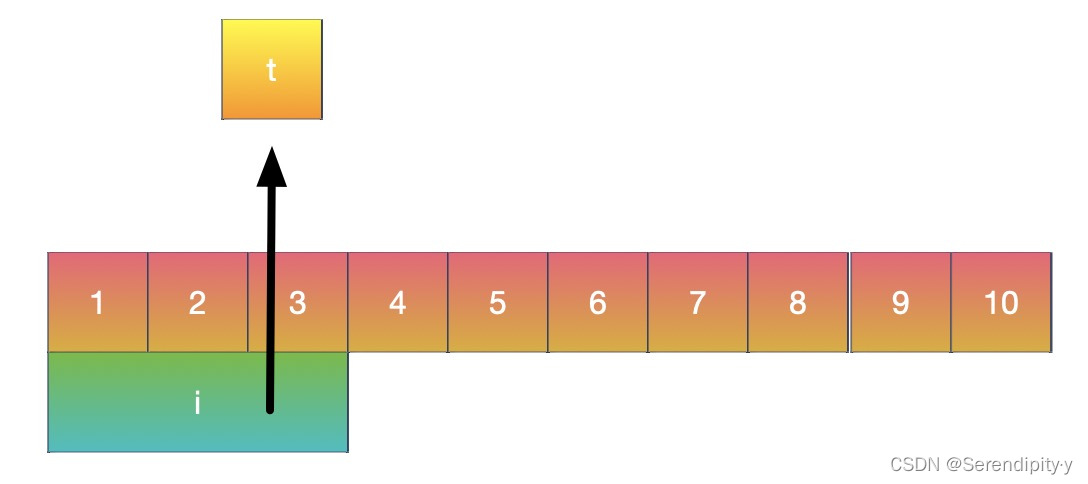
• 右指针开始往后寻找，如果后续的区间的开始值比 t 还小，说明重复了，可以归并到一起；

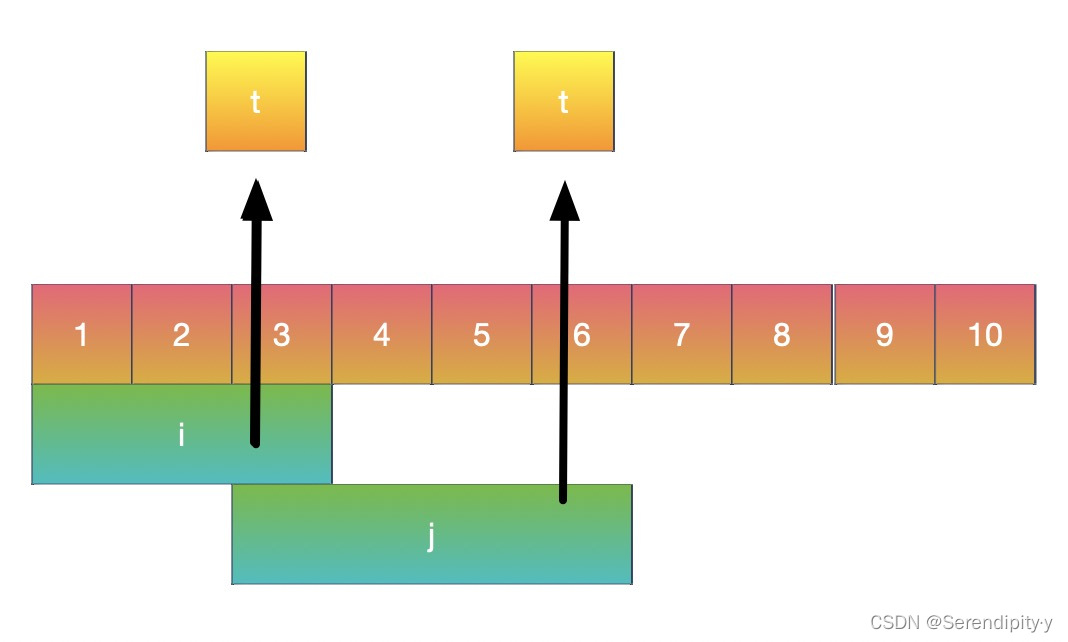
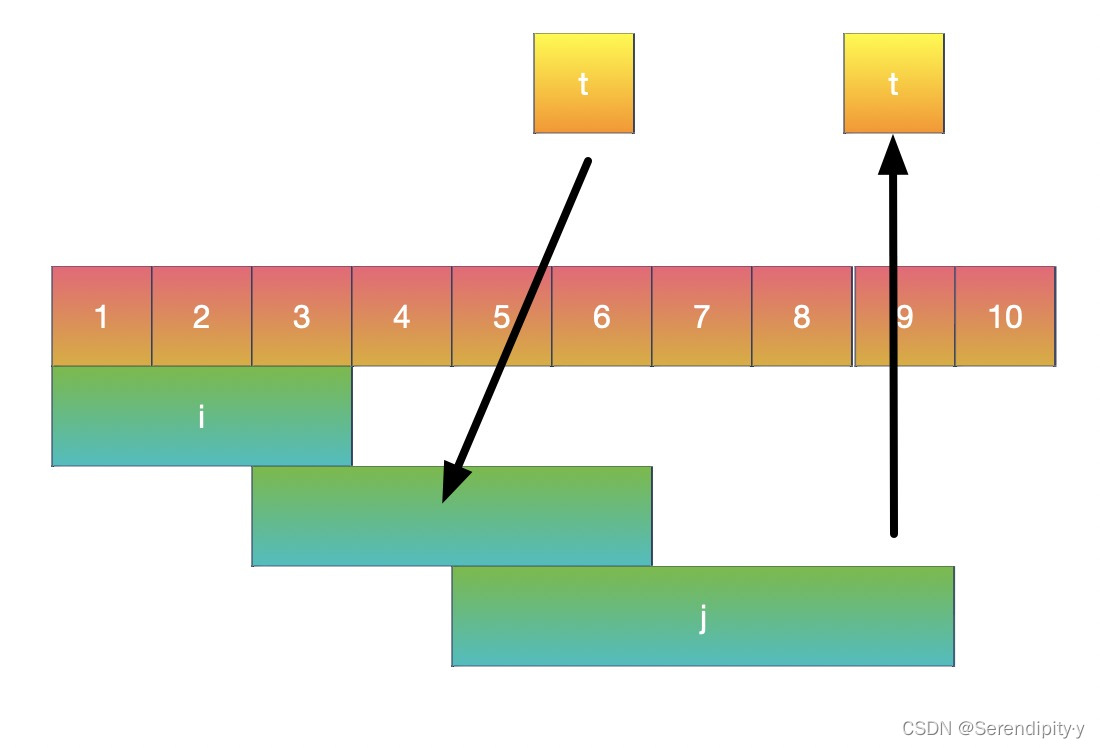
• 此时更新更大的结束值到 t；
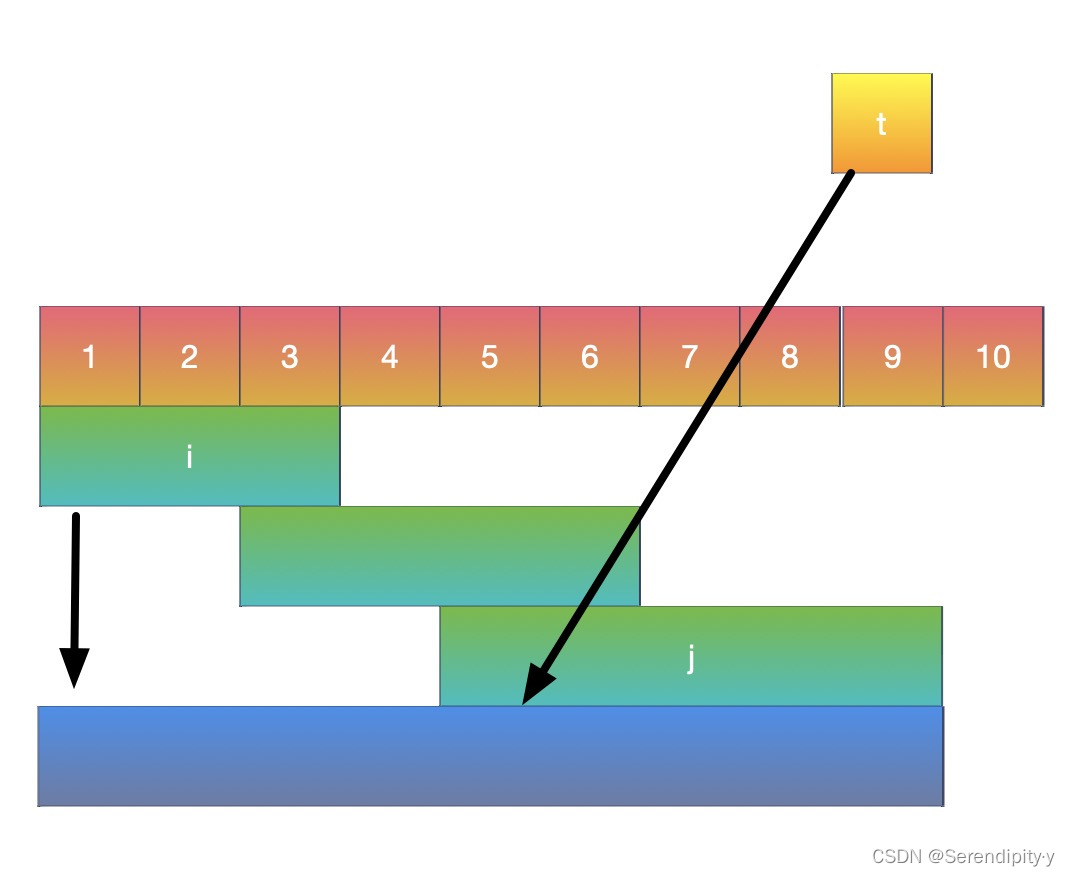
• 直到区间断开，将 t 作为区间结束，存储到答案里；

• 然后移动左指针，跳过中间已经合并的区间。

• C++ 示例：

    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> ans;
        for (int i = 0; i < intervals.size();) {
            int t = intervals[i][1];
            int j = i + 1;
            while (j < intervals.size() && intervals[j][0] <= t) {
                t = max(t, intervals[j][1]);
                j++;
            }
            ans.push_back({ intervals[i][0], t });
            i = j;
        }
        return ans;
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

• Java 示例：

public int[][] merge(int[][] intervals) {
        List<int[]> inter = Arrays.asList(intervals);
        List<int[]> newInter = new ArrayList<>(inter);
        newInter.sort((o1, o2) -> o1[0] - o2[0]);
        
        List<int[]> res = new ArrayList<>();
        for(int i = 0; i < newInter.size(); )
        {
            int t = newInter.get(i)[1];
            int j = i + 1;
            while(j < newInter.size() && newInter.get(j)[0] <= t)
            {
                t = Math.max(t, newInter.get(j)[1]);
                j++;
            }
            res.add(new int[]{newInter.get(i)[0], t});
            i = j;
        }

        int[][] ans = new int[res.size()][2];
        for(int i = 0; i < res.size(); i++)
        {
            ans[i][0] = res.get(i)[0];
            ans[i][1] = res.get(i)[1];
        }
        return ans;
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
 

② 排序（LeetCode 官方解法）

• 如果按照区间的左端点排序，那么在排完序的列表中，可以合并的区间一定是连续的。如下图所示，标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间，它们在排完序的列表中是连续的：

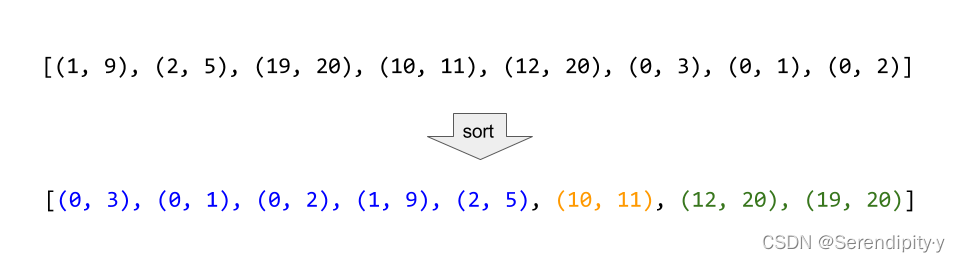
• 用数组 merged 存储最终的答案，将列表中的区间按照左端点升序排序，然后将第一个区间加入 merged 数组中，并按顺序依次考虑之后的每个区间：
• • 如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；
• • 否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。
• 上述算法的正确性可以用反证法来证明：在排完序后的数组中，两个本应合并的区间没能被合并，那么说明存在这样的三元组 (i,j,k) 以及数组中的三个区间 a[i],a[j],a[k] 满足 i<j<k 并且 (a[i],a[k]) 可以合并，但 (a[i],a[j]) 和 (a[j],a[k]) 不能合并。这说明它们满足下面的不等式：

• 联立这些不等式（注意还有一个显然的不等式 a[j].start≤a[j].end），可以得到：

• 产生了矛盾，这说明假设是不成立的。因此，所有能够合并的区间都必然是连续的。
• C++ 示例：

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) {
            return {};
        }
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> merged;
        for (int i = 0; i < intervals.size(); ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (!merged.size() || merged.back()[1] < L) {
                merged.push_back({L, R});
            }
            else {
                merged.back()[1] = max(merged.back()[1], R);
            }
        }
        return merged;
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

• Java 示例：

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0) {
            return new int[0][2];
        }
        Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });
        List<int[]> merged = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
                merged.add(new int[]{L, R});
            } else {
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

文章来源: blog.csdn.net，作者：Serendipity·y，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Forever_wj/article/details/122813016