逻辑点点
apk下载链接:资源分享汇总
游戏规则:把圆点放进一定的方格中,使得每行每列的圆点数目和所给定的数字一样,而且圆点按照相邻的分为一组,分组结果也要和给定的一样
隐含规则:每一组都是1*n的形状,一组和另一组是完全相隔的,即一组的圆点不是另一组的圆点的八邻居
在下面的适当的位置,我依次解释了5个方法:
方法一:极小数字的处理
方法二:极大数字的处理
方法三:各组互斥
方法四:可选组
方法五:对大组位置的枚举
(1)


方法一:极小数字的处理
每个格子最终只有2种状态,放圆点和不放圆点
当一行中已经确定位置的圆点数量达到了该行标定的数字,那么其他格子就都是不放圆点的了,列的话同理。
包括特殊情况:如果数字是0,这一行(列)就直接标注出来不放圆点。
这个看起来没什么用,实际上关键在于已经知道最终状态的一定要先标注出来,对于后面的工作是有影响的。
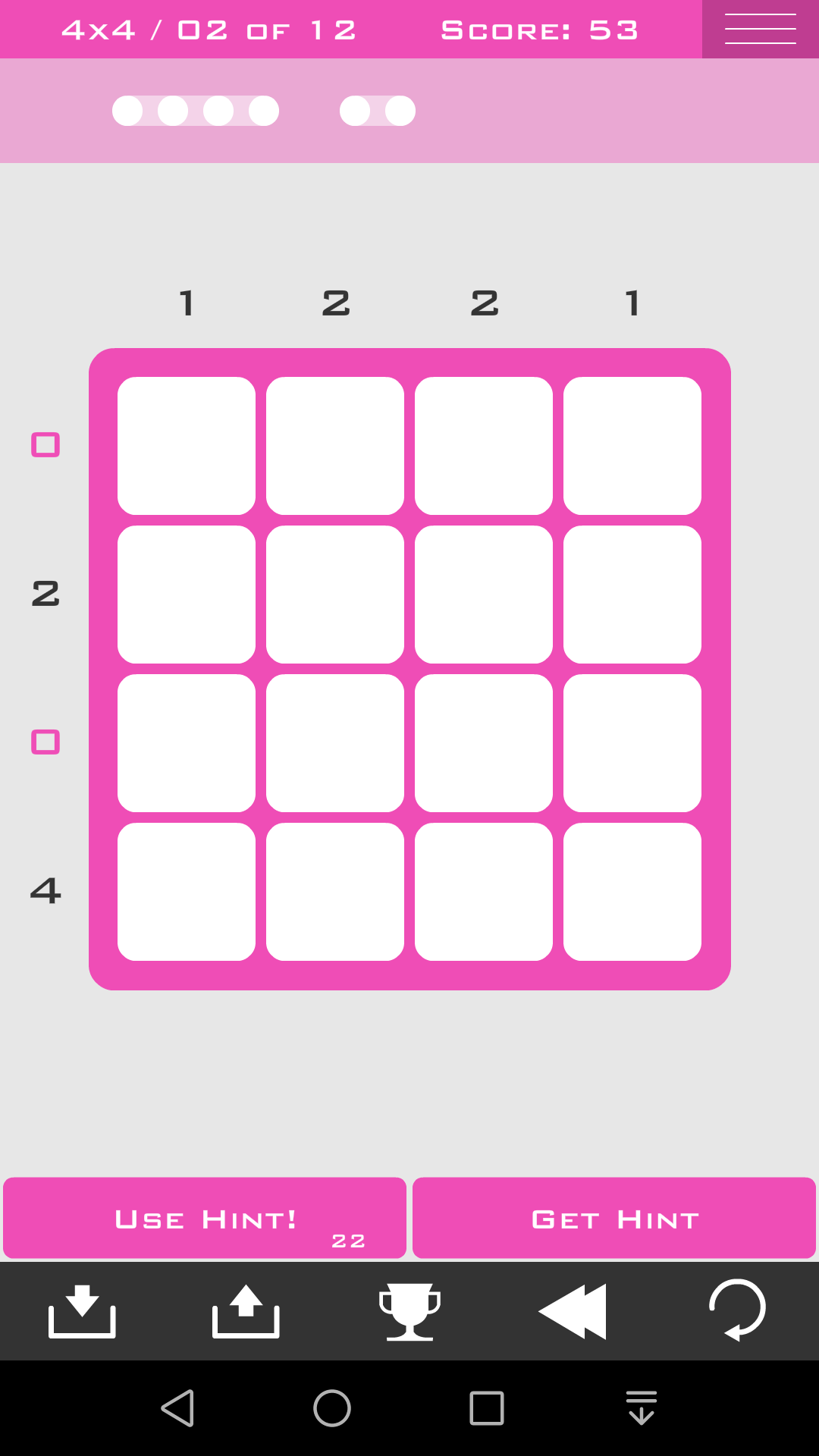
方法二:极大数字的处理:
和极小数字的处理同理,当一行中有可能放圆点(包括确定放圆点)的位置的数量等于这一行标注的数字时,这些格子就一定都是放圆点的,应该立刻标注出来,列的话同理。
包括特殊情况:如果数字是棋盘的长宽size,那么这一行(列)就都放圆点。
(2)

(3)


(4)

(5)


(6)


(7)


(8)

(9)


(10)


(11)


(12)


(1)


(2)


(3)


(4)


(5)


(6)


(7)


(8)


(9)


(10)


(11)


(12)

(13)


(14)


(15)


(16)


(17)


(18)

(19)

(20)


(21)


(22)


(23)


(24)


(25)


(26)

(27)


(28)


(29)

(30)


(1)


(2)


(3)

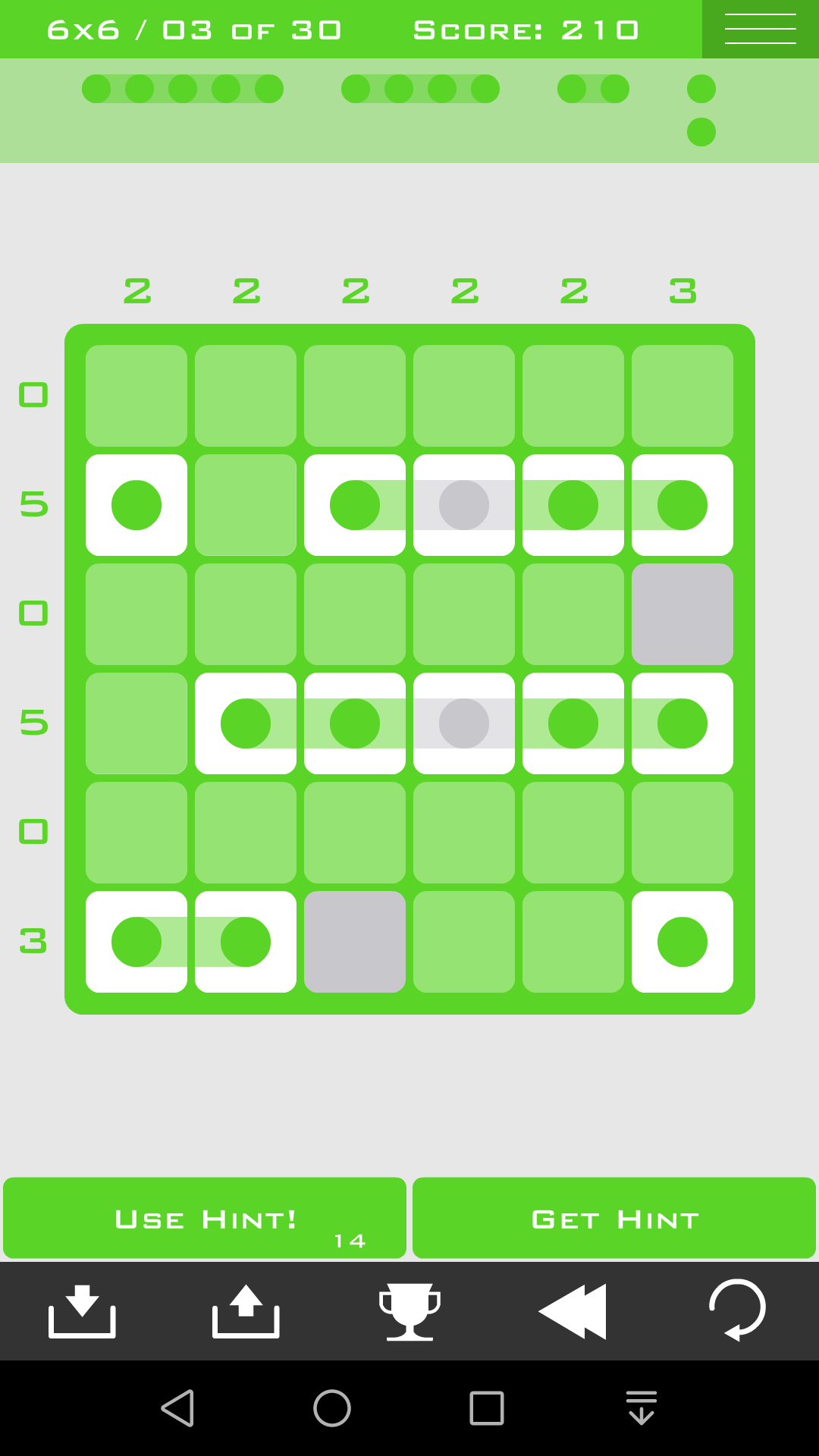
(4)


(5)

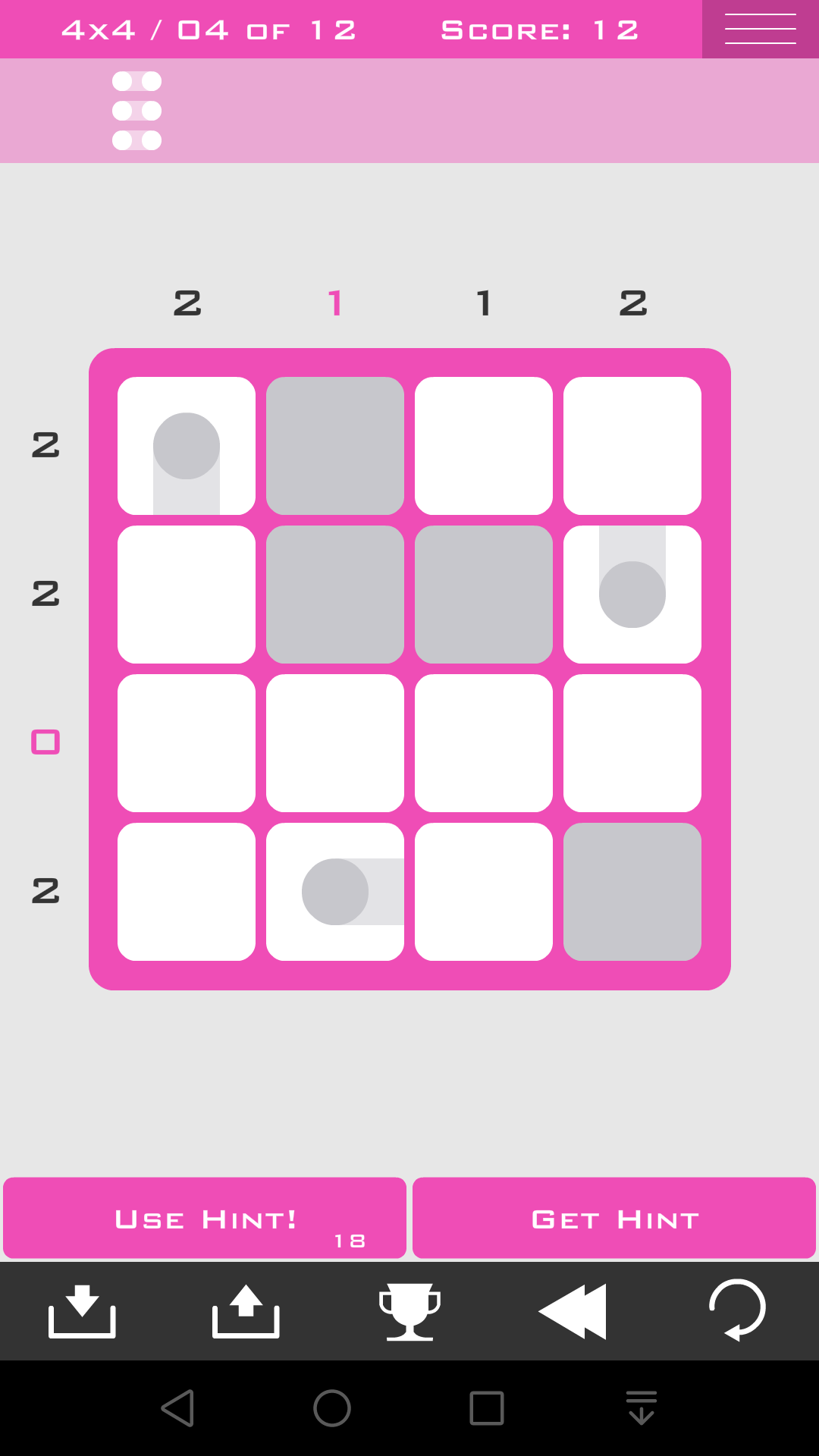
方法三:各组互斥
因为各组是互斥的,所以可以确定一些格子是没有圆点的
为了叙述方便可以分成2种组:
(1)单个圆点构成的组,例如这第(5)关最终会有2个这样的组
单个圆点构成的组,它的八邻居都是不放圆点的
(2)n(n>1)个圆点构成的组,如果确定了这组的方向(可能还没确定该组所有圆点的位置,但是确定了2个圆点的位置即可确定方向是水平还是竖直),那么每个圆点的八邻居中,不在该组所在行列的6个邻居都是不放圆点的

这里标注黑色三角形的圆点,它的邻居中的6个就是不放圆点的,对于超出边界的自然就是直接忽略了
接下来,按照极大数字的处理:

最后:

(6)


(7)


(8)


(9)


(10)

(11)


(12)


(13)


(14)


(15)


(16)


(17)
(18)


(19)


(20)


(21)

注意,虽然格子的最终状态只有2种,但是如果是提示的格子,那么除了给子本身之外,还知道邻居的情况。
其实也就是对《方法三:各组互斥》的拓展。
也就是说刚开始就可以确定的是:

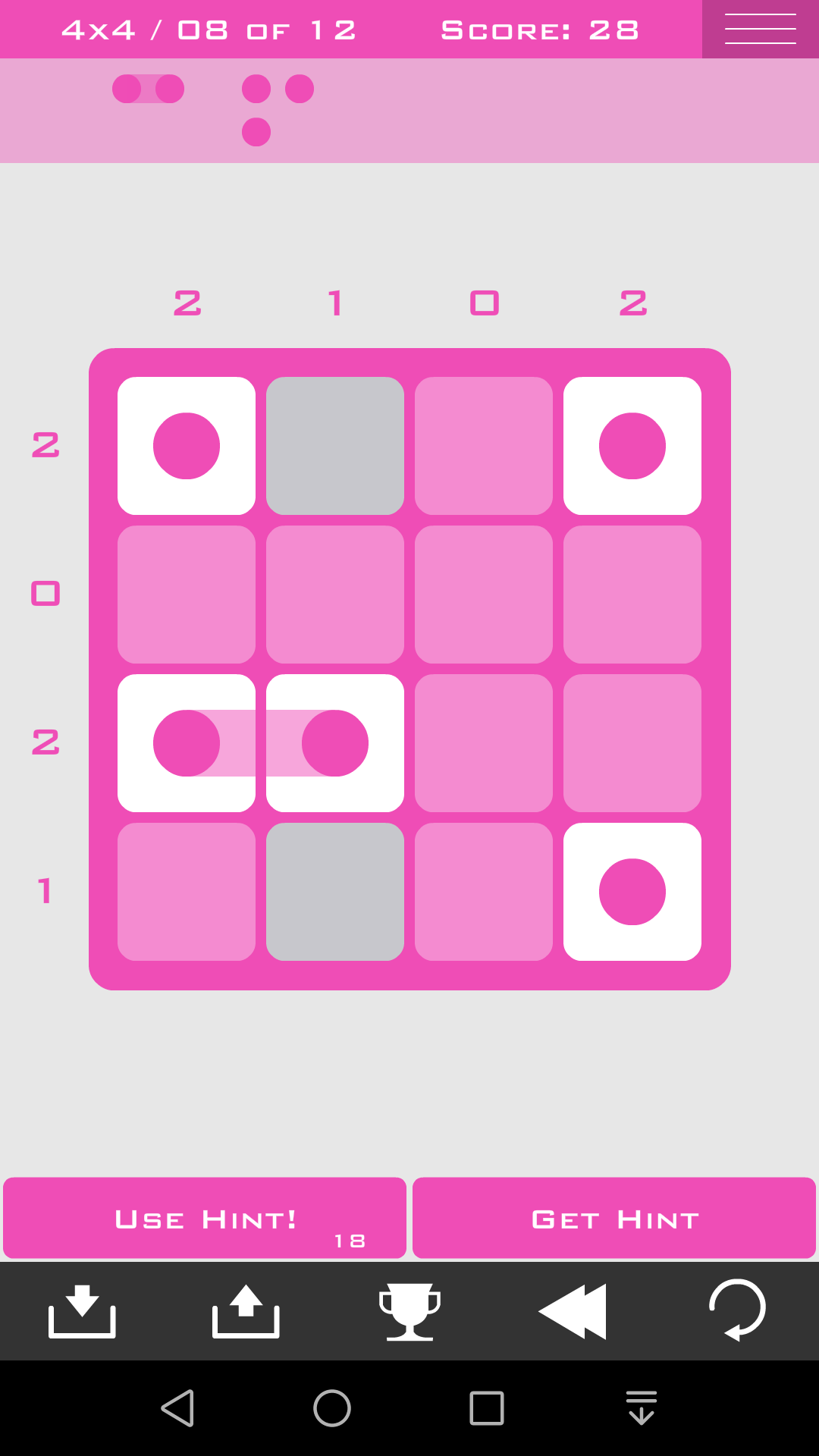
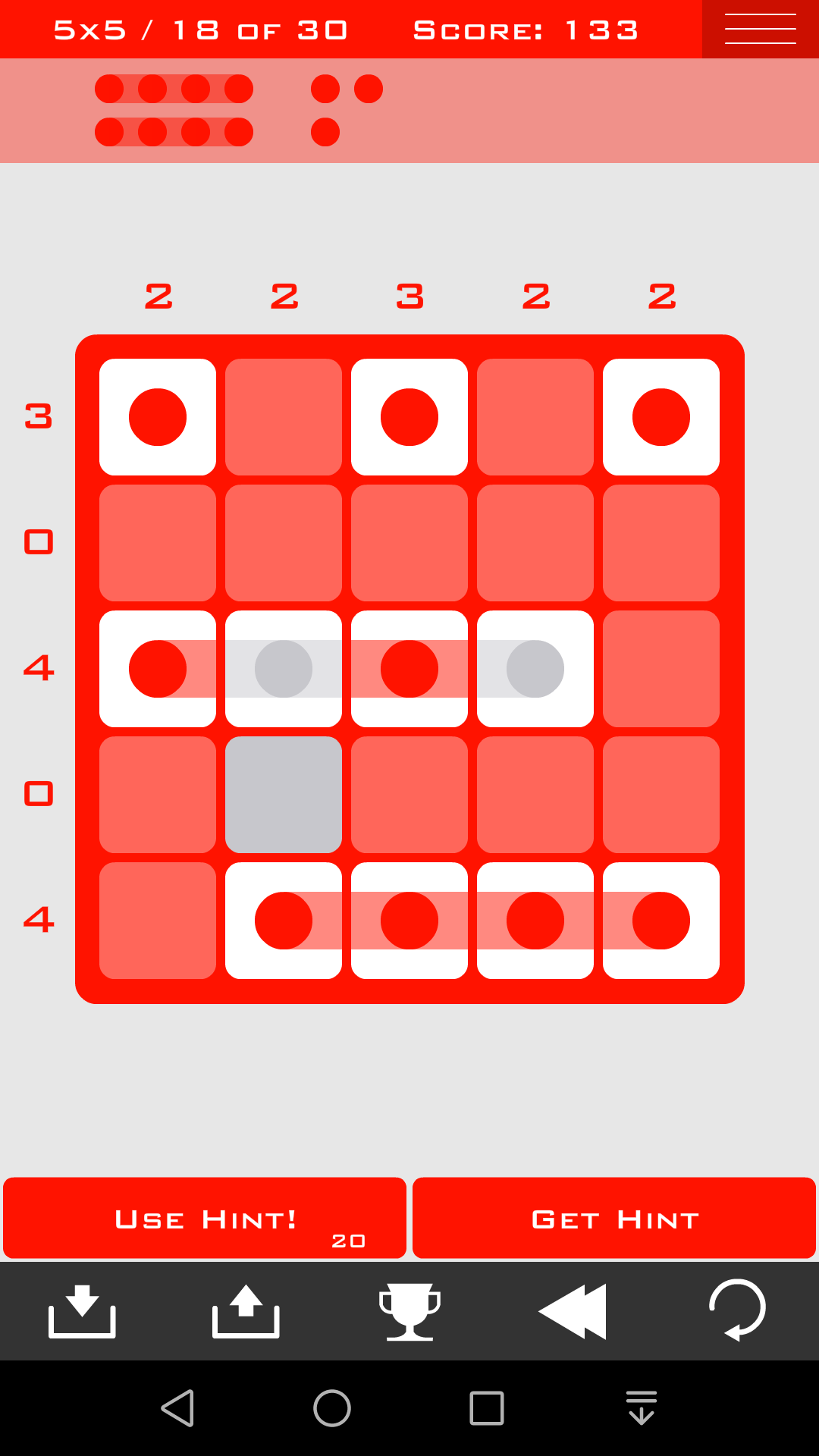
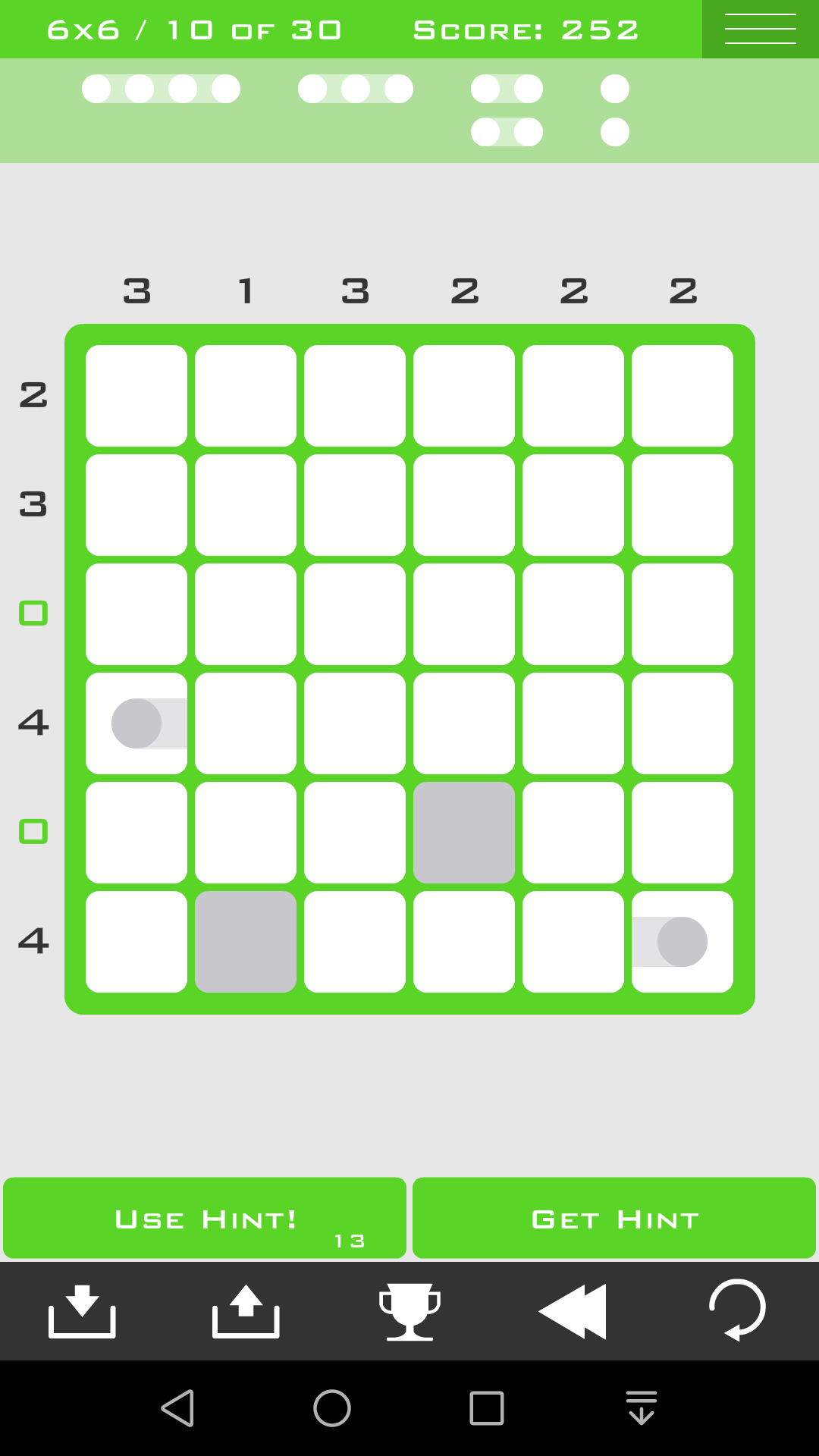
方法四:可选组
如果一行(列)接近完全确定但不能完全确定,可以考虑可选的组的限制
比如这一关,只有1*4的组,没有1*3的组,所以第4行一定是1*4的组

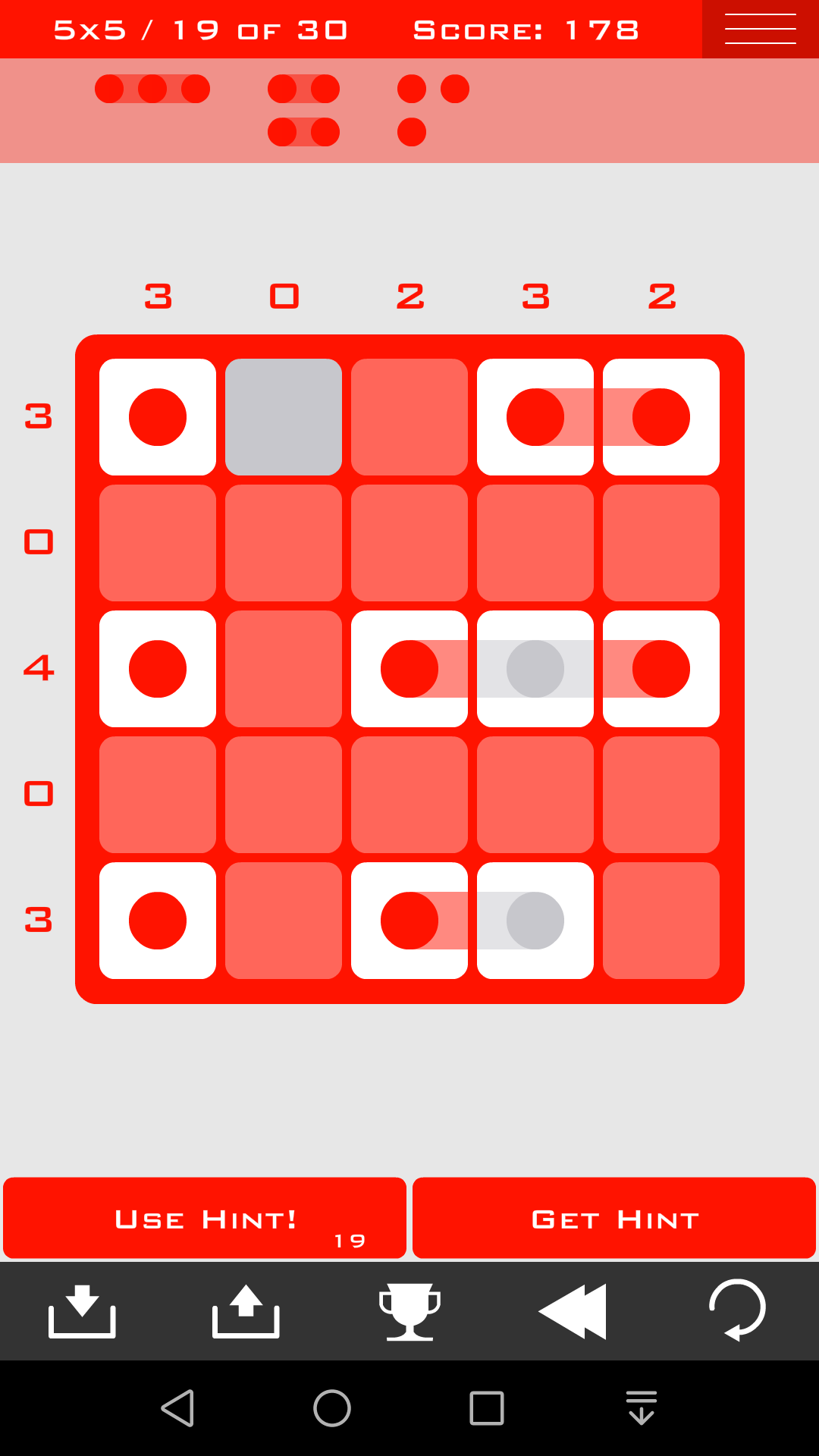
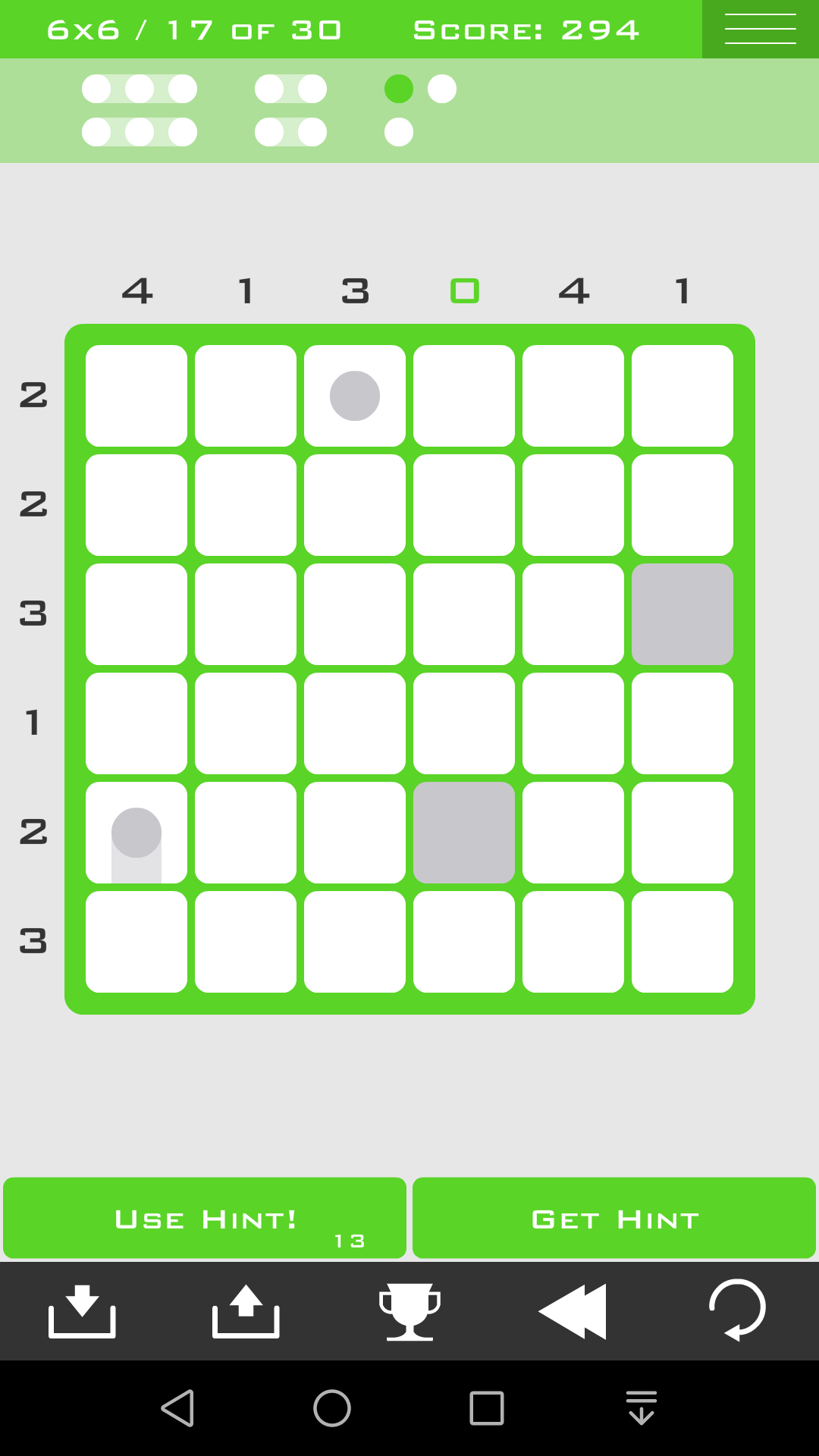
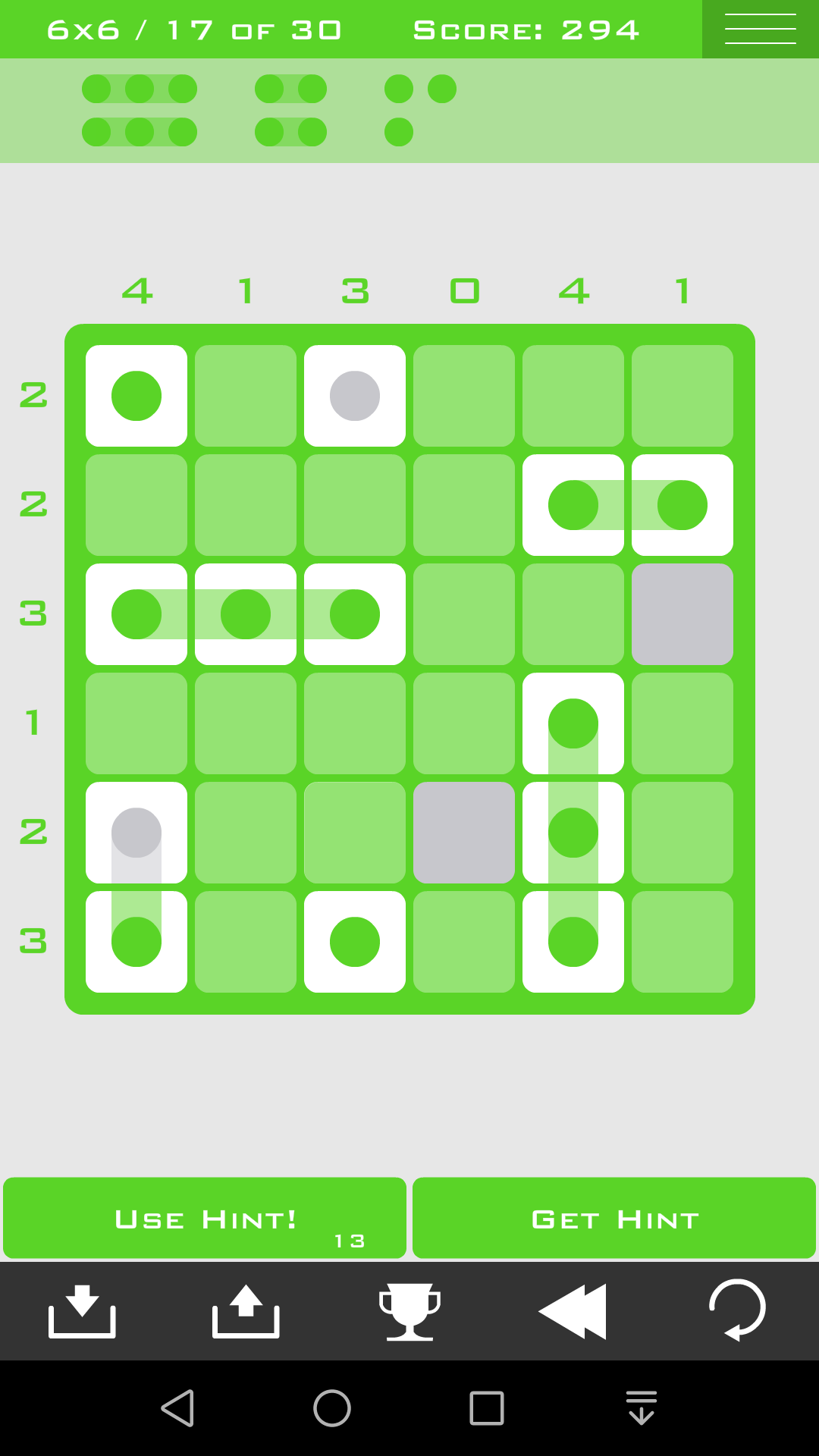
这里继续使用《方法四:可选组》,而且要和《方法三:各组互斥》结合起来
现在只剩下2个1*2的组和2个1*1的组
如果第6行是1*2的组那么第1、2行要放3个组,很明显是无法做到的,
所以第6行一定是2个1*1的组,第1、2行一定是2个1*2的组,而且一横一竖
这样答案就出来了,由于对称性的存在,答案并不唯一
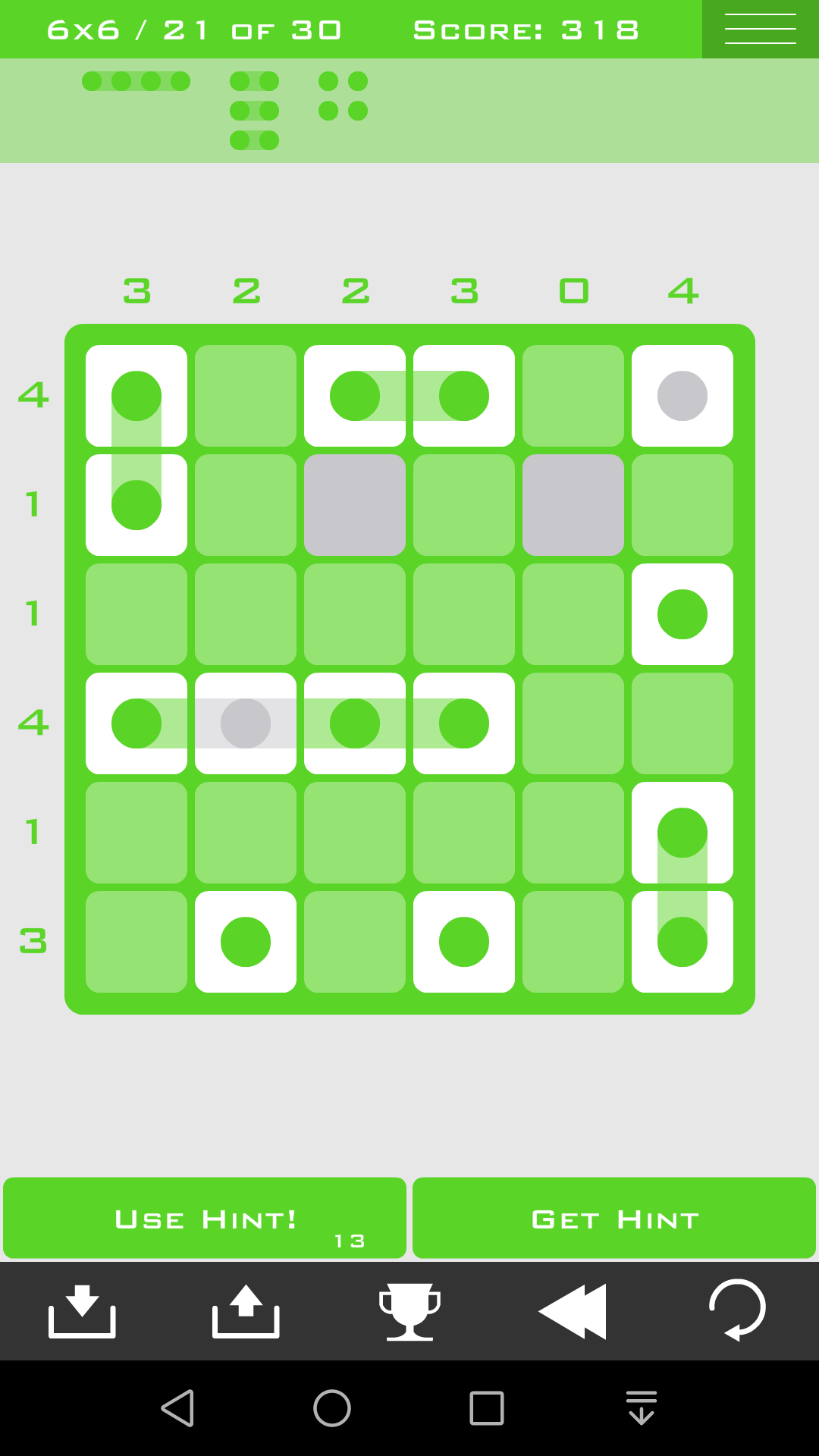
(22)

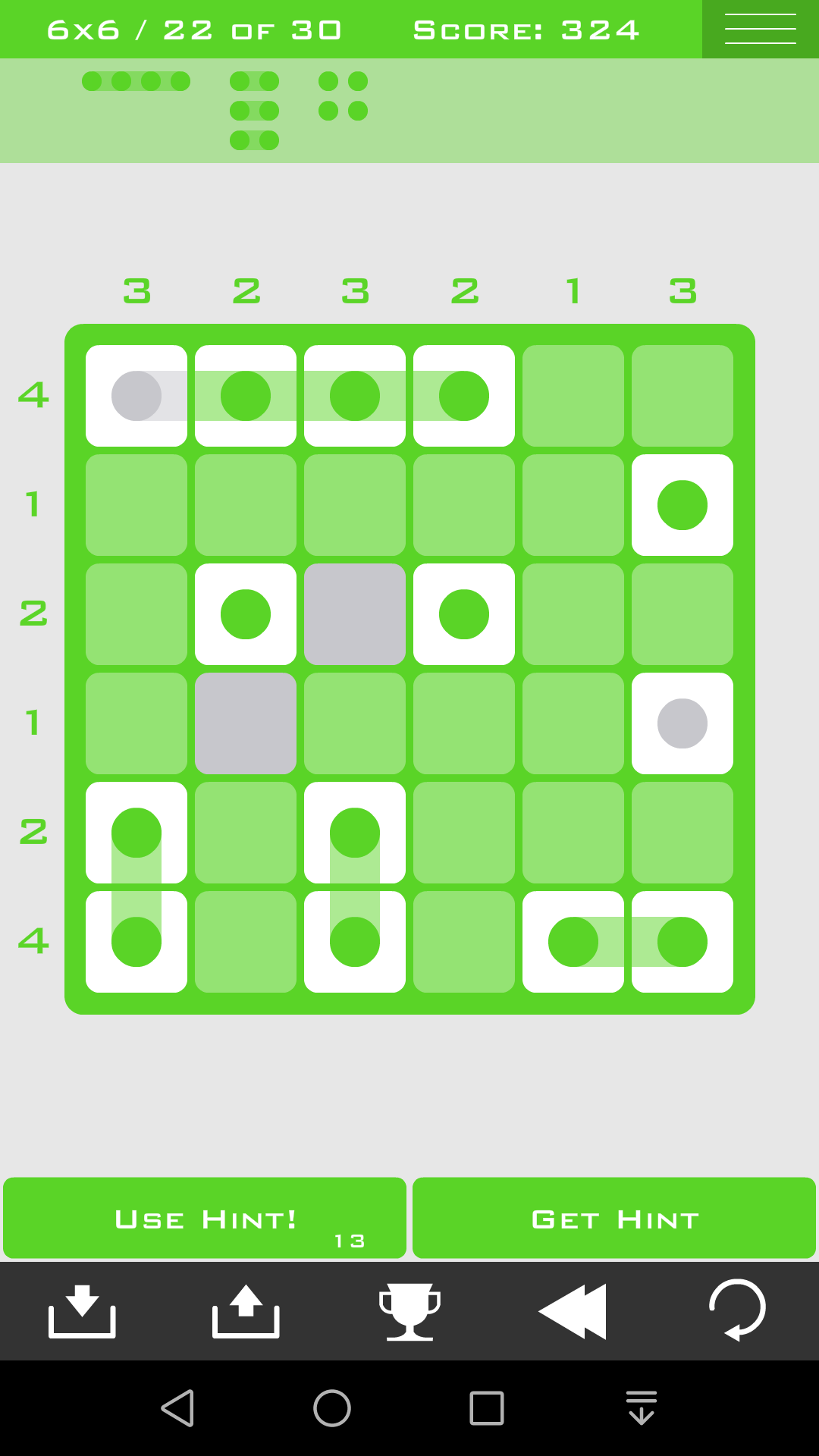
(23)


(24)


(25)


(26)

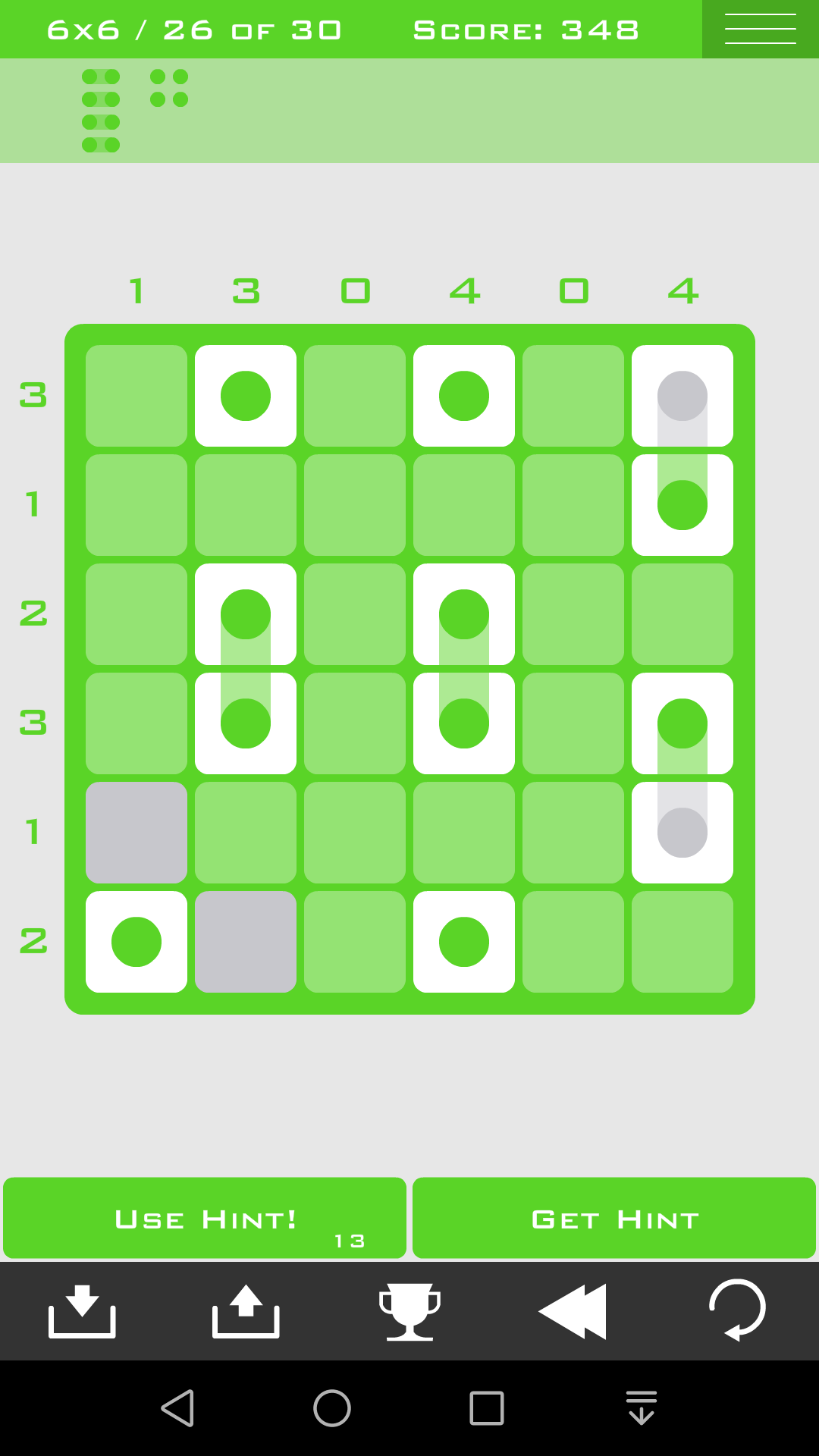
(27)


(28)


(29)


(30)

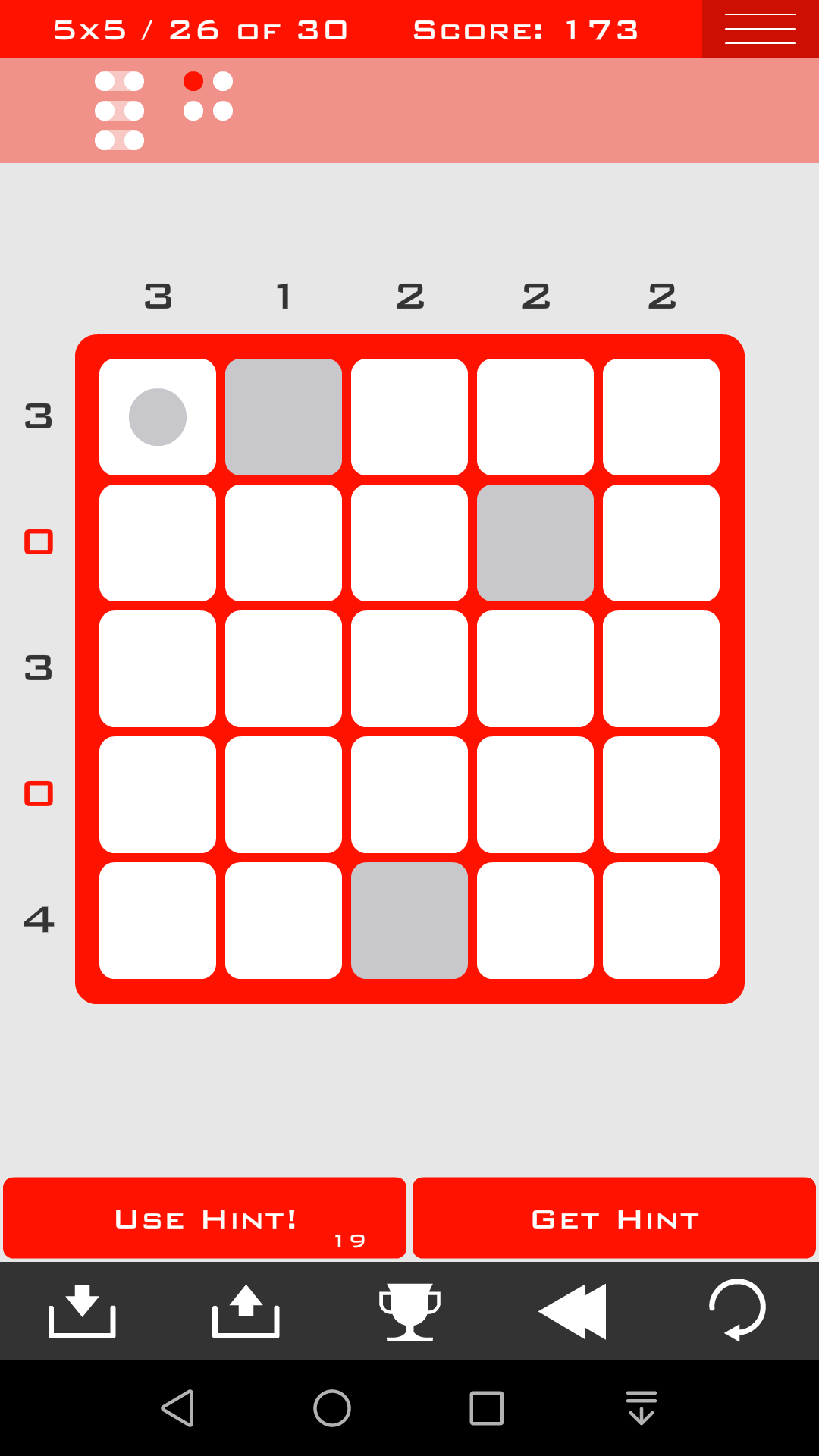
首先还是用方法一二三

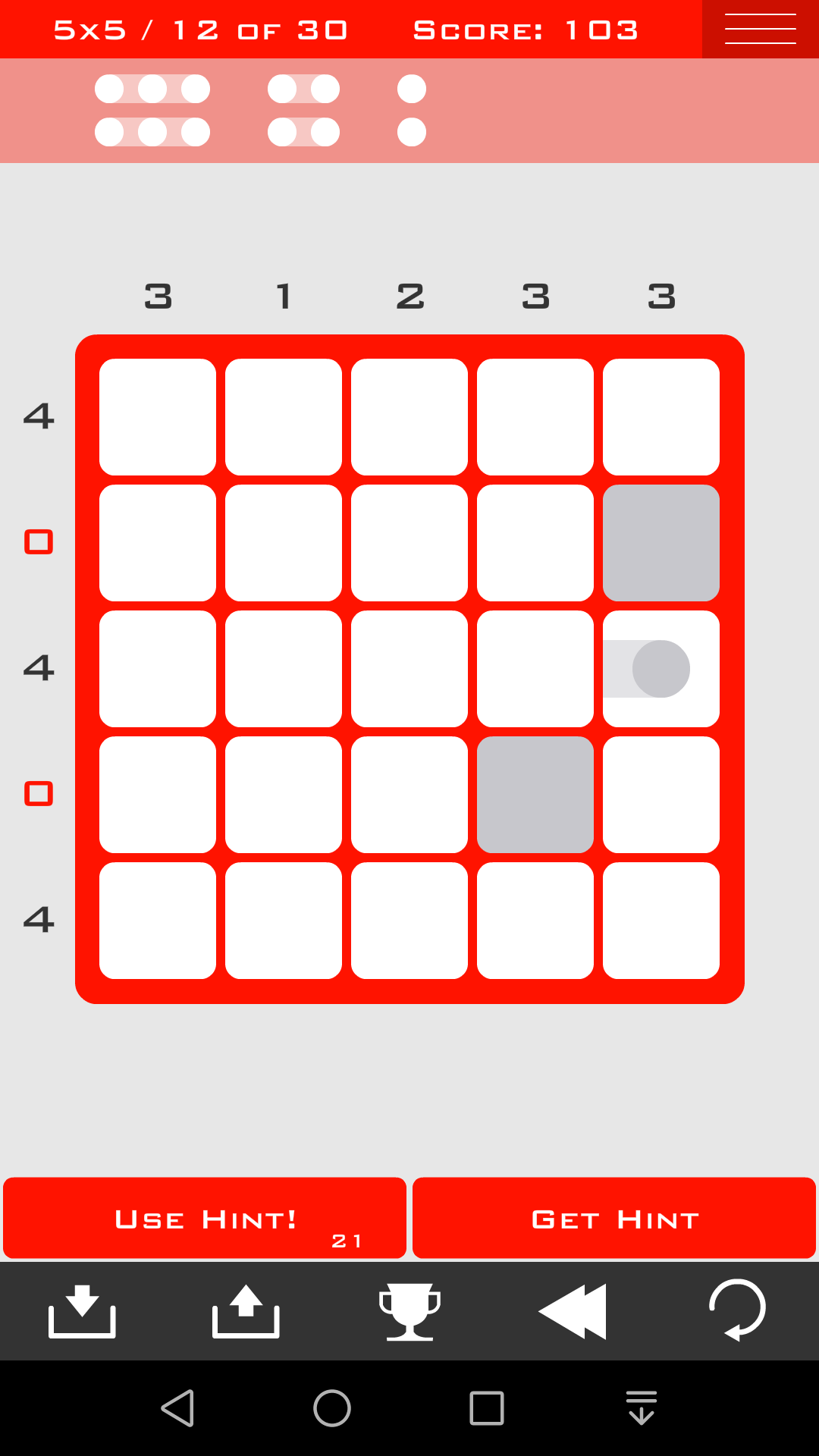
方法五:对大组位置的枚举
考虑最长的那个组怎么放,枚举所有可能的情况
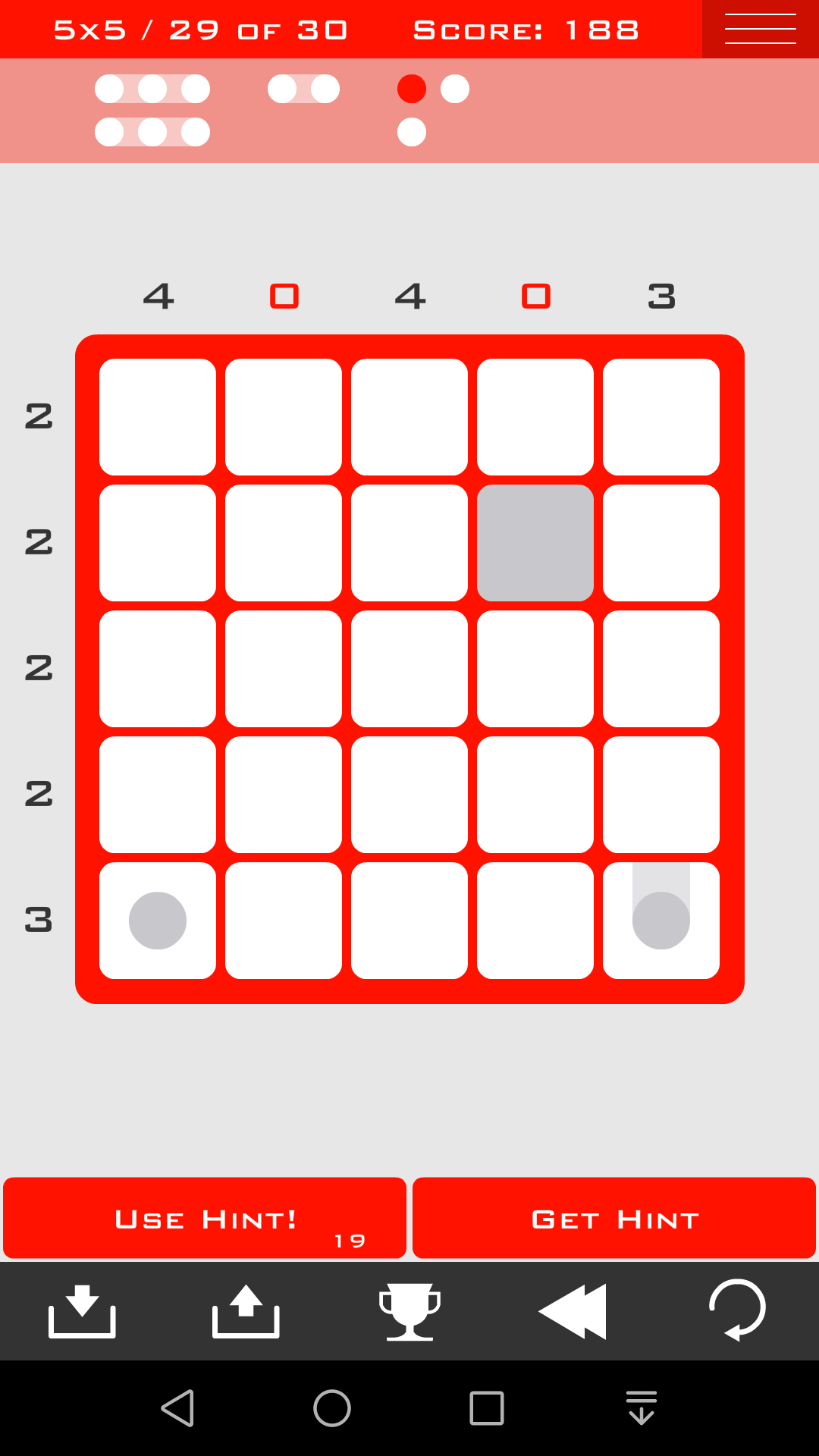
比如这一关,1*3的组肯定是竖着放,而且在第1列或者第3列或者第6列
如果在第1列或者第6列,根据方法一二三很快就能得到,这是无解的
如果在第3列,根据方法一二三很快就能得到解

至此,4*4的,5*5的,6*6的全部通关。
后面还有更大的棋盘,但是需要的方法我已经总结完毕,无非只是计算量大些。
如果计算量过大,还可以编程解决,我的代码在我的另外一篇博客中:战舰系列
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/122905939
- 点赞
- 收藏
- 关注作者


评论(0)