利用 scipy.signal中的spectrogram分析信号的时频联合分布
简 介: 通过时频分布可以分析出时变信号的内部频谱结构的变化。但对于普通的窄带信号,求取的频谱中具有比较高的峰值,在使用普通的热力图显示的时候,过高的峰值数据会将峰值比较小的频谱进行压制。对结果中的过高峰值进行限幅可以凸显结果中的细节。
关键词: spectrogram,DTMF,时频分布
§01 时频分布
1.1 基本概念
利用 时频联合分布 可以方便分析非平稳信号。其中包括两大类:
- 线性视频表示:比如短视Fourier变换,小波变换,Gabor变换等;
- 二次型视频表示,比如功率谱,视频分布等。
典型的视频分布例子有:Page分布、Wigner-ville分布、Choi-Williams分布等等。

▲ 线性调频信号
1.2 分析scipy软件包
利用 scipy.signal.spectrogram 可以非常方便获得信号的时频分布。它是利用STFT来计算信号的时频分布的。
(1)调用方法
scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, mode='psd')
- 1
Ⅰ.参数:
-
x:array_like
测量值的时间序列 -
fs:float, 可选参数
x时间序列的采样频率。默认为1.0。 -
window:str 或 tuple 或 array_like, 可选参数
希望使用的窗口。如果window是字符串或元组,则将其传递给get_window生成窗口值,默认情况下为DFT-even。参考get_window有关窗口和必需参数的列表。如果窗口是数组,它将直接用作窗口,并且其长度必须为nperseg。默认为形状参数为0.25的Tukey窗口。 -
nperseg:int, 可选参数
每个段的长度。默认为无,但是如果window是str或tuple,则设置为256,如果window是数组,则设置为窗口的长度。 -
noverlap:int, 可选参数
段之间重叠的点数。如果没有,noverlap = nperseg // 8。默认为没有。 -
nfft:int, 可选参数
如果需要零填充的FFT,则使用的FFT的长度。如果为None,则FFT长度为nperseg。默认为无。 -
detrend:str 或 function 或 False, 可选参数
指定如何使每个段趋势消失。如果detrend是一个字符串,它将作为类型参数传递给detrend函数。如果它是一个函数,它将采用一个段并返回一个去趋势的段。如果detrend是假,不进行趋势消除。默认为‘constant’。 -
return_onesided:bool, 可选参数
如果为True,则返回真实数据的one-sided频谱。如果为False,则返回two-sided频谱。默认为True,但是对于复杂数据,始终返回two-sided频谱。 -
caling:{ ‘density’, ‘spectrum’ }, 可选参数
如果x的单位为V且fs的单位为fs,则在计算Sxx的单位为V ** 2 /Hz的功率谱密度(‘density’)和计算Sxx的单位为V ** 2的功率谱(‘spectrum’)之间进行选择。赫兹。默认为‘density’。 -
axis:int, 可选参数
计算频谱图的轴;默认值位于最后一个轴上(即axis=-1)。 -
ode:str, 可选参数
定义期望的返回值类型。选项为[‘psd’,‘complex’,‘magnitude’,‘angle’,‘phase’]。 ‘complex’等效于stft没有填充或边界扩展。 ‘magnitude’返回STFT的绝对大小。 ‘angle’和‘phase’分别返回带展开和不展开的STFT的复角。
Ⅱ.返回值:
- f:ndarray
采样频率数组。 - t:ndarray
细分时间数组。 - Sxx:ndarray
x的频谱图。默认情况下,Sxx的最后一个轴对应于段时间。
1.3 问题来源
在 电话双音频拨号声音中的干扰信号 分析了带有干扰的电话双音频干扰信号,对该信号求取Spectrogram,显示他们的时频联合分布对应拨码信号突变时,频谱出现了较大的变化。如下图所示:

▲ 图1.3.1 电话信号中出现三个错误码
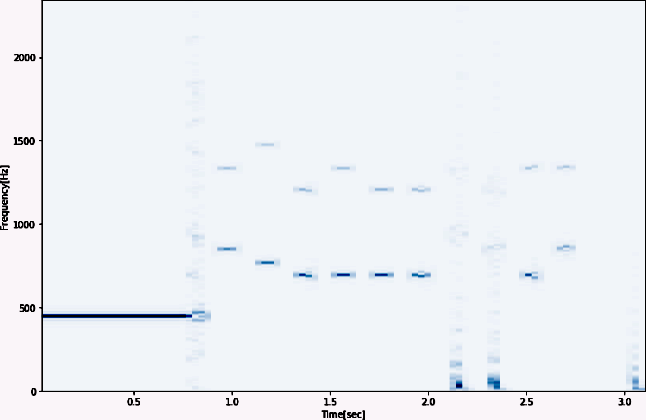
▲ 图1.3.2 对应的Spectrogram对应的频谱
对于这种情况,在 检测DTMF信号中的时间间隔 中分析,应该是该信号在发送的过程中出现的间断。因此,其中的高低频谱应该还是存在的。但是在上面的时频联合分布中可以看到对应的高低频谱线消失。
现在看来应该是在使用 scipy.signal.spectrogram的过程中,使用pcolormesh显示是所使用的参数不对造成显示不清楚。
验证这个结论,在一定程度上,还是为DTMF信号分析提供依据。
§02 分析DTMF信号
2.1 读取显示波形
2.1.1 显示信号波形
import sys,os,math,time
import matplotlib.pyplot as plt
from numpy import *
from scipy.io import wavfile
wavefile = '/home/aistudio/work/ERROR/一次拨号出现三个数字错误.wav'
sample_rate,sig = wavfile.read(wavefile)
print("sample_rate: {}\n".format(sample_rate), "shape(sig): {}\n".format(shape(sig)))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
sample_rate: 8000
shape(sig): (25265,)
- 1
- 2

▲ 图2.1.1 错误三个新号码的信号波形图
plt.clf()
plt.figure(figsize=(10,6))
plt.plot(sig)
plt.xlabel("n")
plt.ylabel("sample")
plt.grid(True)
plt.tight_layout()
plt.savefig('/home/aistudio/stdout.jpg')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
2.1.2 显示信号频谱
由于频谱中存在着谱线,它们的高度会出现很大的差异。如果在同一频谱图将它们绘制出来,那么幅值较小的结构就会看不清楚。
比如下面是对Sxx直接使用pcolormesh进行显示,可以看到马哥电话号码的高频频谱都不太清楚。对于三个受到干扰的拨码对应的频谱几乎消失了。

▲ 图2.1.2 直接显示变换结果
这种情况一开始让我错以为被破坏的信号中的频率也都出现的很大的变化。
如果使用对最高值进行限幅,可以在一定程度上将取值大的数据对于数值小的频谱的压制。
f,t,Sxx = signal.spectrogram(sig, fs=sample_rate, nperseg=512, noverlap=256, nfft=512)
plt.clf()
plt.figure(figsize=(10,6))
startid = 20
endid = 120
threshold = 20000
Sxx[where(Sxx>threshold)] = threshold
plt.pcolormesh(t, f[startid:endid], Sxx[startid:endid,:])
plt.xlabel("Time(s)")
plt.ylabel("Frequency(Hz)")
plt.grid(True)
plt.tight_layout()
plt.savefig('/home/aistudio/stdout.jpg')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
下面是对S写中所有超过20000的数据都使用20000进行限幅,最终显示的热力图。可以看到:
- 原本幅值比较小的高频信号频谱可以比较清晰的显示了;
- 对应波形破坏的三个信号,其中的高低频的分量还是存在的;这验证了拨码信号中间中断的假设。

▲ 图2.1.3 显示的时频联合分布
下面是利用计算机声卡录制的电话拨号信号的时频分布图。对照可以看到它们对应的电话编码是一致的。

▲ 图2.1.4 利用计算机声卡录制的电话双音频信号的时频分布
分析在线信号
在昨天(2022-01-22)利用电话双音频拨码信号采集采集了旧式电话连线后的音频信号。
- 采集信号数据:
-
数据文件:online-wave2.mp3
时间长度:2606秒
格式:MP3
信号波形
import sys,os,math,time
import matplotlib.pyplot as plt
from numpy import *
from scipy.io import wavfile
from scipy import signal
wavefile = '/home/aistudio/work/ONLINE-WAVE2.mp3'
from pydub import AudioSegment
sound = AudioSegment.from_file(file=wavefile)
left = sound.split_to_mono()[0]
sample_rate = sound.frame_rate
sig = frombuffer(left._data, int16)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
startid = int(sample_rate * 2.5)
endid = int(sample_rate * 5.2)
plt.clf()
plt.figure(figsize=(10,6))
plt.plot(sig[startid:endid])
plt.xlabel("n")
plt.ylabel("sample")
plt.grid(True)
plt.tight_layout()
plt.savefig('/home/aistudio/stdout.jpg')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12

▲ 前10秒的数据波形

▲ 图2.2.2 在2.5 ~ 5.2秒之间的数据
信号时频分布
data = sig[startid:endid]
f,t,Sxx = signal.spectrogram(data, fs=sample_rate, nperseg=2048, noverlap=2000, nfft=8192)
threshold= 150000
Sxx[where(Sxx>threshold)]=threshold
plt.clf()
plt.figure(figsize=(10,6))
plt.pcolormesh(t,f[50:350], Sxx[50:350,:])
plt.xlabel("Time(s)")
plt.ylabel("Frequency(Hz)")
plt.grid(True)
plt.tight_layout()
plt.savefig('/home/aistudio/stdout.jpg')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

▲ 图2.2.3 音频信号的时频分析
§总 结
通过时频分布可以分析出时变信号的内部频谱结构的变化。但对于普通的窄带信号,求取的频谱中具有比较高的峰值,在使用普通的热力图显示的时候,过高的峰值数据会将峰值比较小的频谱进行压制。对结果中的过高峰值进行限幅可以凸显结果中的细节。
■ 相关文献链接:
● 相关图表链接:
- 线性调频信号
- 图1.3.1 电话信号中出现三个错误码
- 图1.3.2 对应的Spectrogram对应的频谱
- 图2.1.1 错误三个新号码的信号波形图
- 图2.1.2 直接显示变换结果
- 图2.1.3 显示的时频联合分布
- 图2.1.4 利用计算机声卡录制的电话双音频信号的时频分布
- 前10秒的数据波形
- 图2.2.2 在2.5 ~ 5.2秒之间的数据
- 图2.2.3 音频信号的时频分析
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/122634775
- 点赞
- 收藏
- 关注作者


评论(0)