【蓝桥杯Java_C组·从零开始卷】第六节(二)、蓝桥杯常用数学公式
目录
1、欧几里得定理
package Action;
public class demo {
/*
* 求最大公约数 最小公倍数 思路：根据欧几里得定理 gcd(a,b)=gcd(b,a%b);
*/
static int gcd(int a, int b) {
// 出口：b=0;5和0的最大公约数是5
if (b == 0)
return a;
return gcd(b, a % b);
}
static int lcm(int a, int b) {
return a * b / gcd(a, b);
}
public static void main(String[] args) {
System.out.println(gcd(45, 35));
System.out.println(lcm(45, 35));
System.out.println(gcd(42, 60));
System.out.println(lcm(42, 60));
}
}
2、最大公约数
问题描述
70044与113148的最大公约数是多少？
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
package Action;
public class demo {
public static void main(String[] args) {
int max = 0;
for (int i = 1; i <= 70044; i++) {
if (70044 % i == 0 && 113148 % i == 0) {
max = i;
}
}
System.out.println(max);
}
}
3、最小公倍数
问题描述
已知一个正整数N，问从1~N中任选出三个数，他们的最小公倍数最大可以为多少。
输入格式
输入一个正整数N。
输出格式
输出一个整数，表示你找到的最小公倍数。
样例输入
9
样例输出
504
在一组数中找三个数，使他们的最小公倍数最大。首先，先从两个数的最大公倍数开始，当两个数互质的时候，最小公倍数就是它们的乘积，当然，这也是最大的最小公倍数，所以，拓展到三个数，就是要找出三个两两互质的数。有一个结论我们得先知道，就是相邻的两个自然数是互质的。
一组从1~N的数中，最大的三个数就是N,N-1，N-2,如果这三个数两两互质，那么当然是最大的最小公倍数。
由上面的结论可知，N和N-1，N-1和N-2两两互质。
如果N是奇数，那么N-2也是奇数。那么这两个数不会被2整除，也不会同时被3，5，7，9整除。所以这两个数也两两互质。因此，当N是奇数时，N *（N - 1) * (N - 2）是最大的最小公倍数。
如果N是偶数，显然N和N-2都会被2整除，所以将(N-2)改为（N-3）。如果N不能被3整除，那么最大的最小公倍数为N * (N - 1) * (N -3)。如果N可以被3整除，那么将N改为（N-1），此时最大的最小公倍数为（N - 1）* （N - 2） * （N - 3）。这里（N - 1）为奇数，就跟上一种N是奇数的情况一样。
package Action;
import java.util.Scanner;
public class demo {
public static void main(String[] args) {
@SuppressWarnings("resource")
Scanner sc = new Scanner(System.in);
long n = sc.nextLong();
if (n % 2 == 0) {
if (n % 3 == 0) {
long m = (n - 1) * (n - 2) * (n - 3);
System.out.println(m);
} else {
long m = n * (n - 1) * (n - 3);
System.out.println(m);
}
} else {
long m = n * (n - 1) * (n - 2);
System.out.println(m);
}
}
}
4、海伦公式（求三角形面积）
算法提高 三角形面积
时间限制：1.0s 内存限制：256.0MB
问题描述
由三角形的三边长，求其面积。
提示：由三角形的三边a,b,c求面积可以用如下的公式：
输入格式
由空格分开的三个整数。
输出格式
一个实数，保留两位小数。
样例输入
3 4 5
样例输出
6.00
数据规模和约定
输入的三条边一定能构成三角形，不用进行判定。a,b,c小于1000
package Action;
import java.util.Scanner;
public class demo {
public static void main(String[] args) {
@SuppressWarnings("resource")
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
double l = (a + b + c) * 1.0 / 2;
double s = Math.sqrt(l * (l - a) * (l - b) * (l - c));
System.out.println(String.format("%.2f", s));
}
}
5、排序公式
暂时能想到这些，后面的再补充啊。
- 点赞
- 收藏
- 关注作者
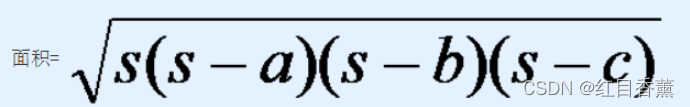
评论（0）