机器学习（十一）岭回归之交通流量预测

（1）线性回归的不足

对于一般地线性回归问题，参数的求解采用的是最小二乘法，其目标函数如下：

参数w的求解，也可以使用如下矩阵方法进行：

（2）岭回归

岭回归的优化目标：

对应的矩阵求解方法为：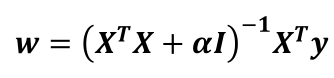

 岭回归(ridge regression)是一种专用于共线性数据分析的有偏估计回归方法
 是一种改良的最小二乘估计法，对某些数据的拟合要强于最小二乘法。

（3）sklearn中的岭回归

在sklearn库中，可以使用sklearn.linear_model.Ridge调用岭回归模型，其主要参数有：
• alpha：正则化因子，对应于损失函数中的𝜶
• fit_intercept：表示是否计算截距，
• solver：设置计算参数的方法，可选参数‘auto’、‘svd’、‘sag’等

（4）交通流量预测实例

数据介绍：
数据为某路口的交通流量监测数据，记录全年小时级别的车流量。
实验目的：
根据已有的数据创建多项式特征，使用岭回归模型代替一般的线性模型，对车流量的信息进行多项式回归。
技术路线：sklearn.linear_model.Ridgefrom
sklearn.preprocessing.PolynomialFeatures

数据特征如下：
HR：一天中的第几个小时（0-23）
WEEK_DAY：一周中的第几天（0-6）
DAY_OF_YEAR：一年中的第几天（1-365）
WEEK_OF_YEAR：一年中的第几周（1-53）
TRAFFIC_COUNT：交通流量
全部数据集包含2万条以上数据（21626）

（5）实验过程

（1）建立工程，导入sklearn相关工具包：

  

   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      from sklearn.linear_model import Ridge
     
    
   

    

     

    
    

     

      #通过sklean.linermodel加载岭回归方法
     
    
   

    

     

    
    

     

      #from sklearn import cross_validation
     
    
   

    

     

    
    

     

      from sklearn import model_selection
     
    
   

    

     

    
    

     

      #加载交叉验证模块，加载matplotilib模块
     
    
   

    

     

    
    

     

      import matplotlib.pyplot as plt
     
    
   

    

     

    
    

     

      from sklearn.preprocessing import PolynomialFeatures
     
    
   

    

     

    
    

     

      #通过..加载..用于创建多项式特征，如ab,a^2,b^2
     
    
  
 

（2）数据加载

  

   

    

     

    
    

     
    #2数据加载
     
    
   

    

     

    
    

     

          data = np.genfromtxt(r'C:\Users\86493\Desktop\北理工机器学习慕课数据\回归\岭回归.txt', delimiter=',')
     
    
   

    

     

    
    

     
    #使用numpy的方法从txt文件中加载数据
     
    
   

    

     

    
    

     

          plt.plot(data[:,4])
     
    
   

    

     

    
    

     
    #使用plt展示车流量信息，如右图
     
    
   

    

     

    
    

     

          plt.show()
     
    
  
 

（3）数据处理

  

   

    

     

    
    

     
    #3数据处理
     
    
   

    

     

    
    

     

          x = data[:,:4]
     
    
   

    

     

    
    

     
    #X用于保存0-4维数据，即属性
     
    
   

    

     

    
    

     

          y = data[:,4]
     
    
   

    

     

    
    

     
    #y用于保存第4维数据，即车流量
     
    
   

    

     

    
    

     

          poly = PolynomialFeatures(9)
     
    
   

    

     

    
    

     
    #用于创建最高次数6次方的多项式特征，多次试验后决定采用6次
     
    
   

    

     

    
    

     

          x = poly.fit_transform(x)
     
    
   

    

     

    
    

     
    #X为创建的多项式特征
     
    
  
 

（4）划分训练集和测试集

  

   

    

     

    
    

     
    #4划分训练集和测试集
     
    
   

    

     

    
    

     

          train_x, test_x, train_y, test_y = \
     
    
   

    

     

    
    

     

          cross_validation.train_test_split(x, y, 
     
    
   

    

     

    
    

     

          test_size=0.3, random_state=0)
     
    
   

    

     

    
    

     
    #将所有数据划分为训练集和测试集,test_size表示测试集的比例
     
    
   

    

     

    
    

     
    #random_state是随机数种子
     
    
  
 

（5）创建回归器，并进行训练

  

   

    

     

    
    

     
    #5创建回归器，进行训练
     
    
   

    

     

    
    

     

          clf = Ridge(alpha=1.0, fit_intercept=True)
     
    
   

    

     

    
    

     
    #接下来创建岭回归实例
     
    
   

    

     

    
    

     

          clf.fit(train_x, train_y)
     
    
   

    

     

    
    

     
    #调用fit函数使用训练集训练回归器
     
    
   

    

     

    
    

     

          score = clf.score(test_x, test_y)
     
    
   

    

     

    
    

     
    #利用测试集计算回归曲线的拟合优度,clf.score返回值为0.7375
     
    
   

    

     

    
    

     
    #拟合优度，用于评价拟合好坏，最大为1，无最小值，当对所有输入都输出一个值时，拟合优度为0
     
    
  
 

（6）画出拟合曲线

  

   

    

     

    
    

     
    #6画出拟合曲线
     
    
   

    

     

    
    

     
    print('score:',score)
     
    
   

    

     

    
    

     

          start = 200
     
    
   

    

     

    
    

     

          end = 300
     
    
   

    

     

    
    

     
    #画一段200到300范围内的拟合曲线
     
    
   

    

     

    
    

     

          y_pre = clf.predict(x) #是调用predict函数的拟合值
     
    
   

    

     

    
    

     

          time = np.arange(start, end)
     
    
   

    

     

    
    

     

          plt.plot(time, y[start:end],'b', label="real")
     
    
   

    

     

    
    

     

          plt.plot(time, y_pre[start:end],'r', label="predict")
     
    
   

    

     

    
    

     
    #展示真实数据(蓝色)以及拟合的曲线(红色)
     
    
   

    

     

    
    

     

          plt.legend(loc="upper left") #设置图例的位置
     
    
   

    

     

    
    

     

          plt.show()
     
    
  
 

全部代码：

  

   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      from sklearn.linear_model import Ridge
     
    
   

    

     

    
    

     

      #通过sklean.linermodel加载岭回归方法
     
    
   

    

     

    
    

     

      #from sklearn import cross_validation
     
    
   

    

     

    
    

     

      from sklearn import model_selection
     
    
   

    

     

    
    

     

      #加载交叉验证模块，加载matplotilib模块
     
    
   

    

     

    
    

     

      import matplotlib.pyplot as plt
     
    
   

    

     

    
    

     

      from sklearn.preprocessing import PolynomialFeatures
     
    
   

    

     

    
    

     

      #通过..加载..用于创建多项式特征，如ab,a^2,b^2
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def main():
     
    
   

    

     

    
    

     
    #2数据加载
     
    
   

    

     

    
    

     

          data = np.genfromtxt(r'C:\Users\86493\Desktop\北理工机器学习慕课数据\回归\岭回归.txt', delimiter=',')
     
    
   

    

     

    
    

     
    #使用numpy的方法从txt文件中加载数据
     
    
   

    

     

    
    

     

          plt.plot(data[:,4])
     
    
   

    

     

    
    

     
    #使用plt展示车流量信息，如右图
     
    
   

    

     

    
    

     

          plt.show()
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
    #3数据处理
     
    
   

    

     

    
    

     

          x = data[:,:4]
     
    
   

    

     

    
    

     
    #X用于保存0-4维数据，即属性
     
    
   

    

     

    
    

     

          y = data[:,4]
     
    
   

    

     

    
    

     
    #y用于保存第4维数据，即车流量
     
    
   

    

     

    
    

     

          poly = PolynomialFeatures(9)
     
    
   

    

     

    
    

     
    #用于创建最高次数6次方的多项式特征，多次试验后决定采用6次
     
    
   

    

     

    
    

     

          x = poly.fit_transform(x)
     
    
   

    

     

    
    

     
    #X为创建的多项式特征
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
    #4划分训练集和测试集
     
    
   

    

     

    
    

     

          train_x, test_x, train_y, test_y = \
     
    
   

    

     

    
    

     

          cross_validation.train_test_split(x, y, 
     
    
   

    

     

    
    

     

          test_size=0.3, random_state=0)
     
    
   

    

     

    
    

     
    #将所有数据划分为训练集和测试集,test_size表示测试集的比例
     
    
   

    

     

    
    

     
    #random_state是随机数种子
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
    #5创建回归器，进行训练
     
    
   

    

     

    
    

     

          clf = Ridge(alpha=1.0, fit_intercept=True)
     
    
   

    

     

    
    

     
    #接下来创建岭回归实例
     
    
   

    

     

    
    

     

          clf.fit(train_x, train_y)
     
    
   

    

     

    
    

     
    #调用fit函数使用训练集训练回归器
     
    
   

    

     

    
    

     

          score = clf.score(test_x, test_y)
     
    
   

    

     

    
    

     
    #利用测试集计算回归曲线的拟合优度,clf.score返回值为0.7375
     
    
   

    

     

    
    

     
    #拟合优度，用于评价拟合好坏，最大为1，无最小值，当对所有输入都输出一个值时，拟合优度为0
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
    #6画出拟合曲线
     
    
   

    

     

    
    

     
    print('score:',score)
     
    
   

    

     

    
    

     

          start = 200
     
    
   

    

     

    
    

     

          end = 300
     
    
   

    

     

    
    

     
    #画一段200到300范围内的拟合曲线
     
    
   

    

     

    
    

     

          y_pre = clf.predict(x) #是调用predict函数的拟合值
     
    
   

    

     

    
    

     

          time = np.arange(start, end)
     
    
   

    

     

    
    

     

          plt.plot(time, y[start:end],'b', label="real")
     
    
   

    

     

    
    

     

          plt.plot(time, y_pre[start:end],'r', label="predict")
     
    
   

    

     

    
    

     
    #展示真实数据(蓝色)以及拟合的曲线(红色)
     
    
   

    

     

    
    

     

          plt.legend(loc="upper left") #设置图例的位置
     
    
   

    

     

    
    

     

          plt.show()
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      if __name__ == '__main__':
     
    
   

    

     

    
    

     

          main()
     
    
  
 

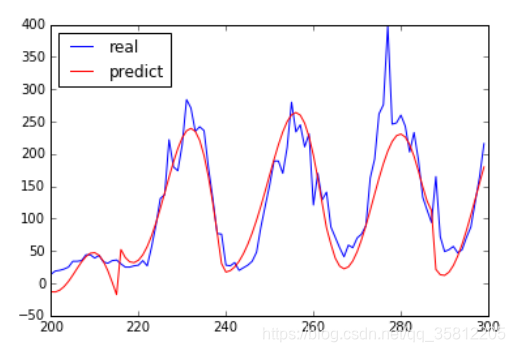
（7）结果分析

分析结论：预测值和实际值的走势大致相同

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/104339854