- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

树-专题模板

野猪佩奇996 发表于 2022/01/23 01:05:33 2022/01/23

【摘要】文章目录 1.基础概念一、几个性质二、二叉树的存储结构 2.二叉树基本操作（1）结点的查找：（2）结点的插入：（3）二叉树的创建 3.遍历（1）层序遍历:（2）统计layer（3）由...

1.基础概念

一、几个性质

（1）森林是若干树的集合，而树是指子结点个数不限且子结点没有先后次序的树（注意二叉树的子结点则是有次序的）。
（2）树可以没有结点（称为空树）。
（3）树的层次（深度）是从根节点（从上往下增大）算的；而树的高度是从底层叶子结点（从下往上增大）算的。
（4）递归边界：地址root为空，即root==NULL（而非*root==NULL），表示这个结点不存在，而括号是指结点存在但内容为NULL（没有内容）。
（5）完全二叉树性质
1.当根结点编号为1时，则编号为x的结点的左孩子的编号为2x，右孩子为2x+1。
2.数组大小设为结点上限个数+1。
3.判断某结点是否为叶结点：
该结点（记下标为root）的左子结点的编号root*2大于结点总个数n（不需要判断右子结点）。
4.判断某结点是否为空结点的标志：
该结点下标root大于结点总个数n。
（6）静态二叉链表的各个操作代码，其实就是结点的左右指针域用int型代替，用来表示左右子树的根结点在数组中的下标。

区别——建立一个大小为结点上限个数的node型数组，所有动态生成的结点都直接使用数组中的结点，所有对指针的操作都改为对数组下标的访问。
（7）平衡二叉树即AVL树是一棵二叉查找树。
只要把最靠近插入结点的失衡结点调整到正常，路径上的所有结点都会平衡。
（8）二叉查找树，即排序二叉树，即二叉排序树，其中序遍历序列是有序的。

二、二叉树的存储结构

二叉链表定义

struct node{
	typename data;
	node* lchild;
	node* rchild;
};

  
 
  1
  2
  3
  4
  5

若用静态二叉链表，则结点的左右指针用int型——表示左右子树的根结点在数组的下标（1、2、3…）

struct node{
	typename data;
	int lchild;
	int rchild;
}Node[maxn];//结点数组，maxn为结点上限个数

  
 
  1
  2
  3
  4
  5

新建结点（如往二叉树中插入结点时）

//生成一个新结点，v为结点权值
node* newNode(int v){
	node* Node=new node;//申请一个node型变量的地址空间
	Node->data=v;
	Node->lchild=Node->rchild=NULL;//初始状态下没有左右孩子
	return Node;//返回新建结点的地址
}

  
 
  1
  2
  3
  4
  5
  6
  7

同理静态二叉链表插入结点：

int index=0;
int newNode(int v){//分配一个Node数组中的结点给新的结点，index为其下标
	Node[index].data=v;
	Node[index].lchild=-1;//以-1或maxn表示空，因为数组范围是0~maxn-1
	Node[index].rchild=-1;
	return index++;
}

  
 
  1
  2
  3
  4
  5
  6
  7

2.二叉树基本操作

（1）结点的查找：

void search(node* root,int x,int newdata){
	if(root==NULL){
		return;//空树，死胡同（递归边界）
	}
	if(root->data==x){
		root->data=newdata;
	}
	search(root->lchild,x,newdata);
	search(root->rchild,x,newdata);
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10

同理，静态二叉链表的写法：

//查找，root为根结点在数组中的下标
void search(int root,int x,int newdata){
	if(root==-1){//用-1代替NULL
		return;//空树，死胡同（递归边界）
	}
	if(Node[root].data==x){
		Node[root].data=newdata;
	}
	search(Node[root].lchild,x,newdata);
	search(Node[root].rchild,x,newdata);
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11

（2）结点的插入：

//insert函数将在二叉树中插入一个数据域为x的新节点
//注意根结点root要使用引用，否则插入不会成功
void insert(node* &root,int x){
	if(root==NULL){
		root=newNode(x);
		return
	}
	if(由二叉树的性质，x应该插在左子树){
		insert(root->lchild,x);
	}else{
		insert(root->rchild,x);
	}
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13

上面代码注意根结点指针root要用引用&——如果不用引用，root=new node对root的修改就无法作用到原变量（即上一层的root->lchild和root->rchild）上去，即不能把新结点接到二叉树上。
加引用——如果函数中需要新建结点（对二叉树的结构修改）就要加引用；如果只是修改当前已有结点的内容，或仅遍历树就不用加引用。

同理，静态二叉链表的插入写法：

//插入，root为根结点在数组中的下标
void insert(int &root,int x){//记得加引用
	if(root==-1){
		root=newNode(x);
		return;
	}
	if(由二叉树的性质，x应该插在左子树){
		insert(Node[root].lchild,x);
	}else{
		insert(Node[root].rchild,x);
	}
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12

（3）二叉树的创建

node* Create(int data[],int n){
	node* root=NULL;//新建空根结点root
	for(int i=0;i<n;i++){
		insert(root,data[i]);
	}
	return root;
}

  
 
  1
  2
  3
  4
  5
  6
  7

同理，静态二叉链表的建树写法：

int Create(int data[],int n){
	int root=-1;//新建空根结点root
	for(int i=0;i<n;i++){
		insert(root,data[i]);
	}
	return root;//返回二叉树的根结点下标
}

  
 
  1
  2
  3
  4
  5
  6
  7

3.遍历

（1）层序遍历:

void LayerOrder(node* root){
    queue<node*> q;//注意队列里是存地址
    q.push(root);//将根结点地址入队
    while(!q.empty()){
        node* now=q.front();//取出队首元素
        q.pop();
        printf("%d ",now->data);//访问队首元素
        if(now->lchild!=NULL) 
            q.push(now->lchild);//左子树非空则加入队列
        if(now->rchild!=NULL)
            q.push(now->rchild);
    }
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13

注意队列中的元素是node*型，而非node。
——因为队列中保存的知识原元素的一个副本，如果队列中直接存放node型，当需要修改队首元素时，就无法对原元素进行修改（只是修改了队列中的副本）。
层序遍历的静态二叉链表写法：

void LayerOrder(int root){
    queue<int> q;//此处队列里存放结点下标
    q.push(root);//将根结点下标入队
    while(!q.empty()){
        int now=q.front();//取出队首元素
        q.pop();
        printf("%d ",Node[now].data);//访问队首元素
        if(Node[now].lchild!=-1) 
            q.push(Node[now].lchild);//左子树非空则加入队列
        if(Node[now].rchild!=-1)
            q.push(Node[now].rchild);
    }
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13

（2）统计layer

在上面层序遍历的基础上添加一个layer的变量。

struct node{
	typename data;
	node* lchild;
	node* rchild;
	int layer;//层次
};

  
 
  1
  2
  3
  4
  5
  6

1.在根结点入队前先令根结点的layer为1，表示根结点是第一层（或者是层号是0，根据题意）。
2.在now->lchild和now->rchild入队前，把它们的层号都记为当前结点now的层号加1。

void LayerOrder(node* root){
    queue<node*> q;//注意队列里是存地址
    root->layer=1;//根结点的层号为1
    q.push(root);//将根结点地址入队
    while(!q.empty()){
        node* now=q.front();//取出队首元素
        q.pop();
        printf("%d ",now->data);//访问队首元素
        if(now->lchild!=NULL) 
            now->lchild->layer=now->layer+1;
            q.push(now->lchild);//左子树非空则加入队列
        if(now->rchild!=NULL)
            now->rchild->layer=now->layer+1;
            q.push(now->rchild);
    }
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16

（3）由先中建树

已知先序遍历序列和中序遍历序列，重建二叉树。
先序序列：
$r o o t = p r e L$ ,
$l e f t = p r e (p r e L + 1) . . . . . . p r e (p r e L + n u m L e f t)$ ,
$r i g h t = p r e (p r e L + n u m L e f t + 1) . . . . . . p r e (p r e R)$
中序序列：
$l e f t = i n (i n L) 、 i n (i n L + 1) 、 . . . i n (k - 1)$ ,
$r o o t = i n (k)$ ,
$r i g h t = i n (k + 1) . . . . . i n (i n R)$

node* create(int preL,int preR,int inL,int inR){
	if(preL>preR){
		return NULL;//先序序列长度小于等于0时，直接返回
	}
	node* root=new node;
	root->data=pre[preL];//先序遍历的第一个结点即根结点
	int k;
	for(k=inL;k<=inR;k++){
		if(in[k]==pre[preL]){//在中序序列中找到根结点的位置，即确定k
			break;
		}
	}
	int numLeft=k-inL;//左子树的结点个数
	
	//左子树的先序区间为[pre+1,pre+numLeft],中序区间为[inL,k-1]
	//返回左子树的根结点地址,赋值给root的左指针
	root->lchild=create(preL+1,pre+numLeft,inL,k-1);
	
	//右子树的先序区间为[pre+numLeft+1,preR]，中序区间为[k+1,inR]
	//返回右子树的根结点地址，赋值给root的右指针
	root->rchild=create(pre+numLeft+1,preR,k+1,inR);
	return root;//返回根结点地址
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23

注意numLeft=k-inL即左子树的结点个数，不用加1。
结论：中序可与先序、后序、层序序列中的任意一个来构建唯一的二叉树（一定要有中序，因为先序、后序、层序均是提供根结点，即作用相同，必须由中序序列来区分出左右子树。）

（4）静态先序

上面已经给出了静态二叉链表的各个操作代码，其实就是用int型代替结点的左右指针域，用来表示左右子树的根结点在数组中的下标。

区别——建立一个大小为结点上限个数的node型数组，所有动态生成的结点都直接使用数组中的结点，所有对指针的操作都改为对数组下标的访问。

void preorder(int root){
	if(root==-1)
		return;
	printf("%d\n",Node[root].data);
	preorder(Node[root].lchild);
	preorder(Node[root].rchild);
}

  
 
  1
  2
  3
  4
  5
  6
  7

4.树

（1）树的静态写法

struct node{
	typename data;
	int child[maxn];//指针域，存放所有子结点的下标
}Node[maxn];//结点数组，maxn为结点上限个数

  
 
  1
  2
  3
  4

由于无法预知子结点个数，所以可以使用变长数组vector定义child数组，即vector<int> child存放所有子结点的下标。
与二叉树的静态实现类似，当需要新建一个结点时，就按顺序从数组中取出一个下标：

int index=0;
int newNode(int v){
	Node[index].data=v;
	Node[index].child.clear();//清空子结点
	return index++;//返回结点下标，并令index自增
}

  
 
  1
  2
  3
  4
  5
  6

不过一般上机考试涉及树（非二叉树）的考察，会给出结点的编号（且结点的编号一定是0、1、…N-1，N为结点个数）——不需要newNode函数，因为题目中给定的编号可以直接作为Node数组的下标使用。

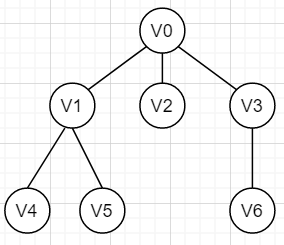
V0:Node[0].child[0]=1,Node[0].child=2,Node[0].child[2]=3;
V1:Node[1].child[0]=4,Node[1].child[1]=5;

  
 
  1
  2

如果题目不涉及结点的数据域（只需要树的结构），可以将一开始树的结构体可以简化成vector数组（去掉结构体元素data），即vector<int> child[maxn]——child[0]、…child[maxn-1]都是一个vector，存放了各结点的所有子结点下标，这种写法其实就是图的邻接表表示法在树中的应用。

（2）先根遍历

树的先根遍历：先访问根结点，再访问所有子树。如按（1）的图先根遍历序列：V0 V1 V4 V5 V2 V3 V6。

void PreOrder(int root){
	printf("%d ",Node[root].data);//访问当前结点
	for(int i=0;i<Node[root].child.size();i++){
		PreOrder(Node[root].child[i]);//递归访问结点root的所有子结点
	}
}

  
 
  1
  2
  3
  4
  5
  6

虽然没写明递归边界，但其实递归边界即for循环的i小于×这个判断。

（3）树层次遍历

思路和二叉树一毛一样，就是while循环内的去除当前结点的所有结点（不只是2个）入队。

void LayerOrder(int root){
    queue<int> q;//此处队列里存放结点下标
    q.push(root);//将根结点下标入队
    while(!q.empty()){
        int now=q.front();//取出队首元素
        q.pop();
        printf("%d ",Node[now].data);//访问队首元素
        for(int i=0;i<Node[front].child.size();i++){
        	Q.push(Node[front].child[i]);//将当前结点的所有子结点入队
        }
    }
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12

（4）层次遍历layer

不止有左右结点，所以就在二叉树版本上将结构体元素改为child数组：

struct node{
	int layer;
	int data;
	vector<int> child;
}

  
 
  1
  2
  3
  4
  5

同理在根结点入队前，对根结点的层号赋初值；对当前结点的所有子结点入队前，对他们的层号加1。

void LayerOrder(int root){
    queue<int> q;//此处队列里存放结点下标
    q.push(root);//将根结点下标入队
    Node[root].layer=0;//记根结点层号为0
    while(!q.empty()){
        int now=q.front();//取出队首元素
        q.pop();
        printf("%d ",Node[now].data);//访问队首元素
        for(int i=0;i<Node[front].child.size();i++){
        	int child=Node[front].child[i];//当前结点的第i个子结点的编号
        	//子结点层号为当前结点层号加1
        	Node[child].layer=Node[front].layer+1;
        	q.push(child);//将当前结点的所有子结点入队
        }
    }
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16

注意上面的这两句：
int child=Node[front].child[i]
Node[child].layer=Node[front].layer+1
搞清楚child为当前结点的孩子结点数组下标编号即可，然后将当前结点的子结点入队前要【提前】将子结点的层数+1。

（5）小结：

（1）对树的DFS遍历就是该树的先根遍历的过程。
（2）可以用DFS做的题，可以把一些状态作为树的结点，问题就会转换为对树进行先根遍历的问题。
（3）如果想要得到树的某些信息，可用DFS获得结果，如求解叶子结点的带权路径和（从根结点到叶子结点的路径上的结点点权之和）时就可以把到达死胡同作为一条路径结束的判断。
（4）树的BFS即层序遍历。

5.二叉查找树

根据BST的性质，查找操作，是从树根到查找结点的一条路径。插入操作就在查找失败的地方插入即可，

void search(node* root,int x){
	if(root==NULL){//空树，查找失败
		printf("Search failed\n");
		return;
	}
	if(x==root->data){//查找成功，访问之
		printf("%d\n",root->data);
	}else if(x<root->data){//如果x比根结点的数据域小，说明x在左子树
		search(root->lchild,x);//往左子树搜索x
	}else{//如果x比根结点的数据域大，说明x在右子树
		search(root->rchild,x);
	}
}

  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/112692032

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入