1.并查集

（1）并查集定义

1.顾名思义，分为三个步骤——并（Union）、查（Find）、集（Set），即并查集支持【合并两个集合】和【查找】操作，查找指判断2个元素是否在一个集合中。
2.集合的判定——对于同一个集合来说只存在一个根结点，且将其作为所属集合的标识。
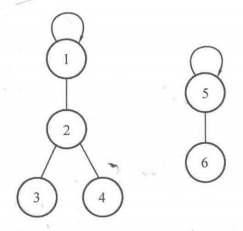
3.int father[N]，其中father[i]标识元素i的父亲结点，而父亲结点本身也是这个集合内的元素，如father[1]=2表示元素1的父亲结点是元素2。

father[1]=1;
father[2]=1;
father[3]=2;
father[4]=2;
father[5]=5;
father[6]=5;

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

上面的定义即1、2、3、4为一个集合，其中元素1位该集合的根结点，而5和6为另外的一个集合，其中元素5是该集合的根结点。
4.若2个元素在相同的集合中，则不会对他们进行合并，从而保证在同一个集合中一定不会产生环，即并查集产生的每个集合都是一颗树。

（2）第一步：初始化

初始时，每个元素都是独立的一个集合，即for循环初始化所有的father[i]=i。

for(int i=0;i<=N;i++){
	father[i]=i;//令father[i]为-1也可以的
}

  

 

  
1
  
2
  
3
 

（3）第二步：查找

//findFather函数返回元素x所在集合的根结点
int findFather(int x){
	while(x!=father[x]){//如果不是根结点，继续循环
		x=father[x];//获得自己的父亲结点
	}
	return x;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

如上图中要查元素4的根结点是谁，
1.x=4,father[4]=2,不相同所以继续查：获得4的父亲结点即2；
2.x=2,father[2]=1,不相同所以继续查：获得2的父亲结点即1；
3.x=1,father[1]=1,相同即找到根结点，返回1.
如果用递归实现如下：

int findFather(int x){
	if(x==father[x])  return x;//如果找到根结点，则返回根结点编号x
	else return findFather(father[x]);//否则，递归判断x的父亲结点是否根结点
}

  

 

  
1
  
2
  
3
  
4
 

（4）合并

即将2个集合合并为1个集合——把一个集合的根结点的父结点指向另一个集合的根结点。
两步走：
【1】利用findFather函数找出各自根结点（是看否相同）从而判断给定的2个元素a和b是否为同一集合。
【2】合并：把其中的一个集合的父结点faA指向另一个集合的父结点faB，即father[faA]=faB。

void Union(int a,int b){
	int faA=findFather(a);
	int faB=findFather(b);
	if(faA!=faB){//如果不属于同一个集合
		father[faA]=faB;
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

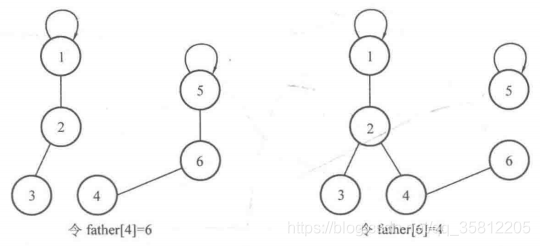
注意father[a]=b不能实现合并，如上图的father[4]=6或father[6]=4，则会得到下面的效果（不能实现集合的合并）。

2.路径压缩（优化）

并查集的路径压缩——把当前查询结点的路径上的所有结点的父亲都指向根结点。
查找就不需要一直回溯去找父结点了。
优化的过程：
（1）按原先的写法获得x的根结点r；
（2）重新从x开始走一遍寻找根结点的过程，把路径上经过的所有结点的父亲全部改为根结点r。
在查找时把寻找根结点的路径压缩：

int findFather(int x){
	//由于x在下面的while中会变成根结点，因此先把原先的x保存一下
	int a=x;
	while(x!=father[x]){//寻找根结点
		x=father[x];
	}
	//到这里，x存放的是根结点，下面把路径上的所有结点的father都改成根结点
	while(a!=father[a]){
		int z=a;//因为a要被father[a]覆盖，所有先保存a的值，以修改father[a]
		a=father[a];//a回溯父结点
		father[z]=x;//将原先的结点a的父亲改为根结点x
	}
	return x;//返回根结点
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

可以把路径压缩后的并查集查找函数均摊效率为O(1)，
另外递归版本如下：

int findFather(int v){
	if(v==father[v])
		return v;
	else{
		int F=findFather(father[v]);//递归寻找father[v]的根结点F
		father[v]=F;//将根结点F赋值给father[v]
		return F;//返回根结点F
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

3.栗子

【好朋友】
有一个叫做“数码世界”奇异空间，在数码世界里生活着许许多多的数码宝贝，其中有些数码宝贝之间可能是好朋友，并且数码宝贝世界有两条不成文的规定：

第一，数码宝贝A和数码宝贝B是好朋友等价于数码宝贝B与数码宝贝A是好朋友

第二，如果数码宝贝A和数码宝贝C是好朋友，而数码宝贝B和数码宝贝C也是好朋友，那么A和B也是好朋友。
现在给出这些数码宝贝中所有好朋友的信息，问：可以把这些数码宝贝分成多少组，满足每组中的任意两个数码宝贝都是好朋友，而且任意两组之间的数码宝贝都不是好朋友。

输入格式：输入的第一行有2个正整数n和m（分别表示数码宝贝的个数和好朋友的组数）
接下来有m行（每行有2个正整数a和b，表示数码宝贝a和数码宝贝b是好朋友）。

4 2
1 4 
2 3

  

 

  
1
  
2
  
3
 

输出格式：输出一个这些数码宝贝可以分成的组数。

2

  

 

  
1
 

（1）思路

在输入这些好朋友关系时就同时对他们进行并查集的合并操作，处理后就能得到一些集合。
对同一个集合来说只存在一个根结点，且将其作为所属集合的标识。
——开一个bool型数组falg[N]来记录每个结点是否作为某个集合的根结点，这样当处理完输入数据后就能遍历所有元素，令它所在集合的根结点的flag值设为true，
最后累加flag数组中的元素既可以得到集合数目。

（2）代码

#include<cstdio>
#include<iostream>
using namespace std;
const int N=110;
int father[N];//存放父结点
bool isRoot[N];//记录每个结点是否作为某个集合的根结点
int findFather(int x){
	//由于x在下面的while中会变成根结点，因此先把原先的x保存一下
	int a=x;
	while(x!=father[x]){//寻找根结点
		x=father[x];
	}
	//到这里，x存放的是根结点，下面把路径上的所有结点的father都改成根结点
	//路径压缩可不写
	while(a!=father[a]){
		int z=a;//因为a要被father[a]覆盖，所有先保存a的值，以修改father[a]
		a=father[a];//a回溯父结点
		father[z]=x;//将原先的结点a的父亲改为根结点x
	}
	return x;//返回根结点
}
void Union(int a,int b){
	int faA=findFather(a);
	int faB=findFather(b);
	if(faA!=faB){//如果不属于同一个集合
		father[faA]=faB;
	}
}
void init(int n){
	for(int i=1;i<=n;i++){
		father[i]=i;
		isRoot[i]=false;//一开始默认每个结点都非根结点
	}
}
int main(){
		int num,groupnum;
		int a,b;//一组中的2个好朋友
		scanf("%d%d",&num,&groupnum);
		init(num);
		//输入两个好朋友的关系(for循环依次合并)
		for(int i=0;i<groupnum;i++){
			scanf("%d%d",&a,&b);
			Union(a,b);
		}
		//令所有结点的父结点为数组下标的isRoot[]=1
		for(int i=1;i<=num;i++){
			isRoot[findFather(i)]=true;
		}
		int ans=0;
		for(int i=1;i<=num;i++){
			ans+=isRoot[i];
		}
		printf("%d\n",ans);
		system("pause");
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
 

其他快方法：https://blog.csdn.net/DedicateToAI/article/details/103039223
PS：如果要求每个集合中元素的数目，则只要把isRoot数组类型设为int即可。

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/112792816