1.题目

2.法一：二分查找

上界为0，下界为x（可以直接写为x/2+1），二分查找。
（1）mid=(left+right)/2，为了防止2个数之和过大，造成溢出，也可以写成left+(right-left)/2，或者除二用移位运算——int mid=left+((right-left)>>1)，注意后面这块需要加个括号（因为位运算的优先级更低）。

（2）mid*mid显然不能用int了（否则可能溢出），要用long long强制类型转换。

（3）如果找到精确结果则返回，最后返回的right实现返回的是舍去小数部分的整数。

class Solution {
public:
    int mySqrt(int x) {
        if(x<=1){
            return x;
        }
        int left=0,right=x/2+1;
        while(left<=right){
            int mid=left+(right-left)/2;
            //int mid=(left+right)/2;
            long long temp=(long long)mid*mid;
            if(temp==x){
                return mid;
            }else if(temp<x){
                left=mid+1;
            }else{
                right=mid-1;
            }
        }
        return right;
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

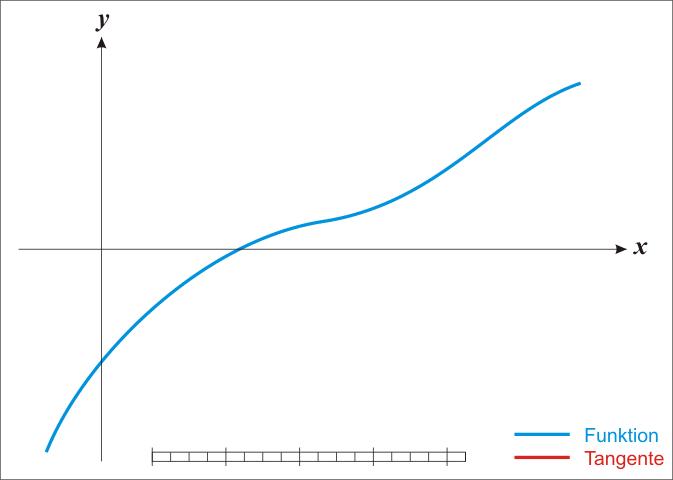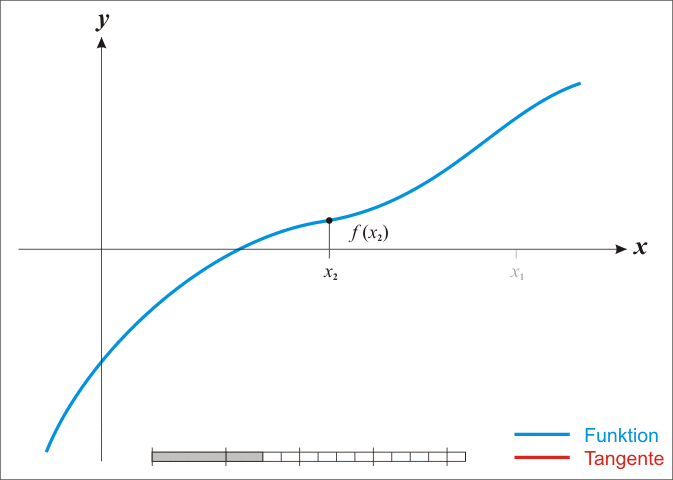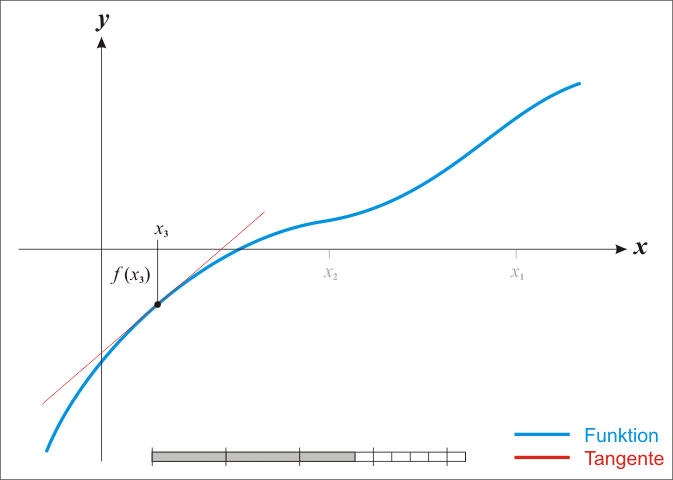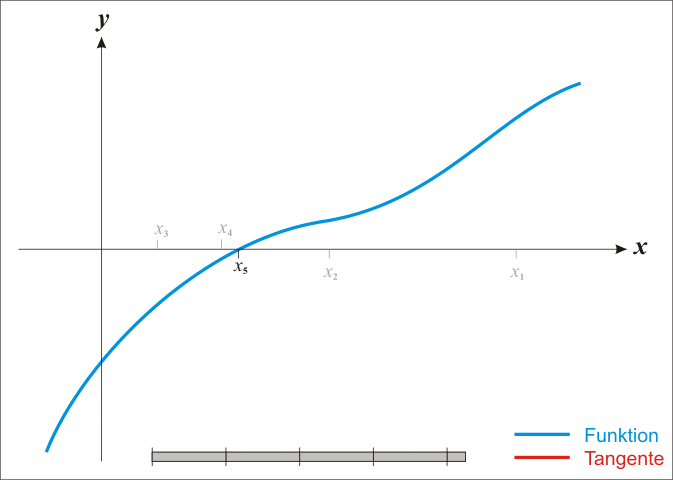
3.法二：牛顿迭代法

在数值分析这门课有牛顿迭代法求开根号，通过递推式$Xm=Xn-f(Xn)/f^{\prime }(Xn)$，其中$m=n+1$，不断迭代得到近似值。

（1）迭代结束标志：
当相邻两次迭代得到的交点非常接近，一般绝对值为10 ^ -6或 10 ^ -7都可以。

（2）选用x0=C作初始点：
从右边开始迭代才能优先得到根号C，如果从0开始迭代则会优先得到负根号C。

class Solution {
public:
    int mySqrt(int x) {
        if(x<=1){
            return x;
        }
        double C=x,x0=x;
        while(true){
            double xi=(x0+C/x0)*0.5;
            if(fabs(x0-xi)<1e-7){
                break;
            }
            x0=xi;
        }
        return int(x0);
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

4.reference

https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95#/media/File:NewtonIteration_Ani.gif

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/113943383