1.题目

2.思路

简单dp。
（1）确定状态：
最后一步：无论机器人用什么方式到达右下角，最后的一步肯定是向右或者向下，即右下角坐标为$(m-1,n-1)$时，机器人前一步一定是在$(m-2,n-1)$或$(m-1,n-2)$。
子问题：如下面所说。
状态：设$f[i][j]$为机器人从左上角走到$(i,j)$。

（2）转移方程：

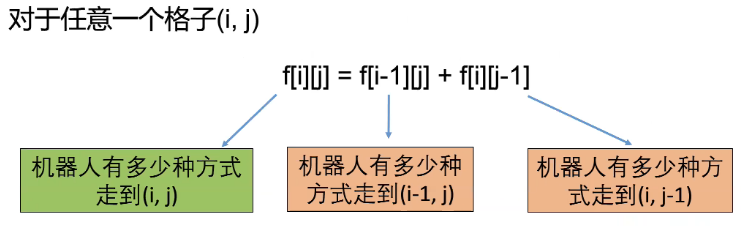
（3）初始条件+边界情况：
初始条件：$f[0][0]=1$，即机器人只有一种方式到左上角（原地不动）。
边界情况：i=0或j=0，则前进一步只能有一个方向（一种方式）过来，即$f[i][j]=1$。

（4）计算顺序：
数组下标m、n都是从0到m-1或者n-1，而最后的答案是$f[m-1][n-1]$。

时间复杂度（求步数）：O(mn)，空间复杂度（数组大小）：O(mn)。

3.代码

class Solution {
public:
    int uniquePaths(int m, int n) {
       int f[m][n];
       for(int i=0;i<m;i++){
           for(int j=0;j<n;j++){
               if(i==0||j==0){
                   f[i][j]=1;
               }else{
                   f[i][j]=f[i-1][j]+f[i][j-1];
               }
           }
       }
       return f[m-1][n-1];
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/113006849