1.题目

DFS 是一个劲的往某一个方向搜索，而回溯算法建立在 DFS 基础之上的，但不同的是在搜索过程中，达到结束条件后，恢复状态，回溯上一层，再次搜索。因此回溯算法与 DFS 的区别就是有无状态重置.
当问题需要 “回头”，以此来查找出所有的解的时候，使用回溯算法。

PS:怎么样写回溯算法
①画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
②根据题意，确立结束条件
③找准选择列表(与函数参数相关),与第一步紧密关联※
④判断是否需要剪枝
⑤作出选择，递归调用，进入下一层
⑥撤销选择
。
。
回溯有两种写法：（下图来自力扣笨猪爆破组）

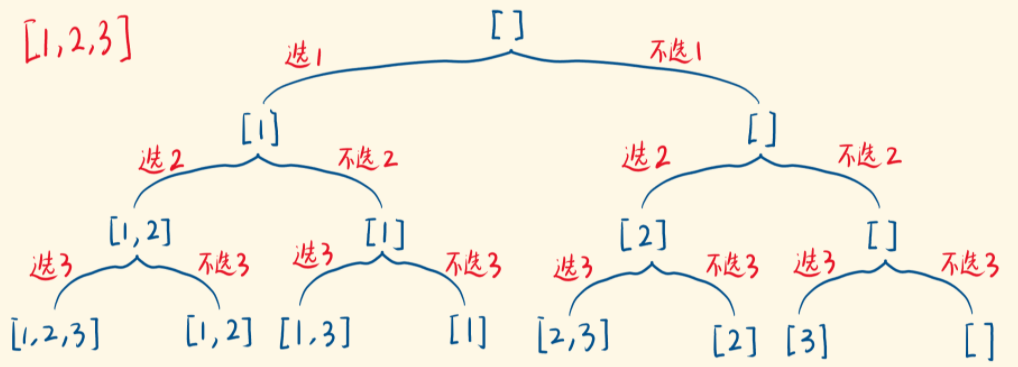
2.法一：二叉树

逐个考察数字，每个数都选或不选。等到递归结束时，把集合加入解集。

class Solution {
private:
    vector<vector<int>>ans;
    vector<int>temp;
public:
    void dfs(int i,vector<int>&nums){
        if(i==nums.size()){
            ans.push_back(temp);
            return;
        }
        //选择第i个数
        temp.push_back(nums[i]);
        dfs(i+1,nums);
        temp.pop_back();
        //不选择第i个数
        dfs(i+1,nums);
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(0,nums);
        return ans;
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

时间复杂度

法一：由二叉树可知，对于每个结点的左右孩子结点（即两个分叉口，为选或者不选），时间复杂度为$O(2^n)$。

3.法二：多叉树（打星号）

在执行子递归之前，加入解集，即，在递归压栈前完成加入解集这一事情。

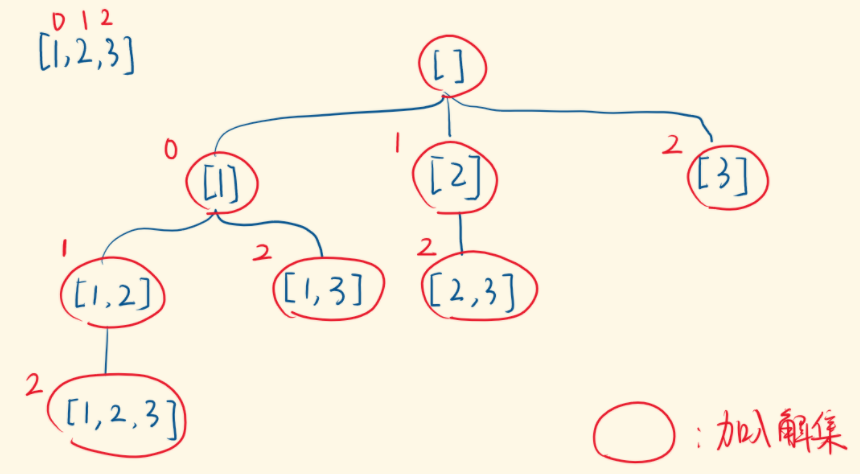
用 for 枚举出当前可选的数，比如选第一个数时：1、2、3 可选。
如果第一个数选 1，选第二个数，2、3 可选；
如果第一个数选 2，选第二个数，只有 3 可选（不能选1，产生重复组合）
如果第一个数选 3，没有第二个数可选

每次传入子递归的 index 是：当前你选的数的索引+1。
每次递归枚举的选项变少，一直递归到没有可选的数字，进入不了for循环，落入不了递归，整个DFS结束。
没有显式地设置递归的出口，而是通过控制循环的起点，使得最后递归自然结束。
主要代码如下：

void backtrack(vector<int>nums,vector<int>&path,int start)
{
    res.push_back(path);
    for(int i=start;i<nums.size();i++)
    {
        path.push_back(nums[i]);//做出选择
        backtrack(nums,path,i+1);//递归进入下一层，注意i+1，标识下一个选择列表的开始位置，最重要的一步
        path.pop_back();//撤销选择
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

reference

笨猪爆破组用户-leetcode题解

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/115532593