学习总结

（1）本次task学习Embedding中的Deep Walk和Node2vec算法，和Embedding在推荐系统的三种应用：直接应用、预训练应用和End2End训练应用。
（2）Deep Walk算法：
1）首先基于原始的用户行为序列来构建物品关系图；
2）采用随机游走的方式随机选择起始点，重新产生物品序列；
3）将2）这些随机游走生成的物品序列输入Word2vec模型，生成最终的物品Embedding向量。
（3）Node2vec相比于Deep Walk，增加了随机游走过程中跳转概率的倾向性：如果倾向于BFS，则Embedding结果更加体现【结构性】，即结构相近的节点的embedding应该接近；如果倾向于DFS，则更加体现【同质性】，即距离相近的节点的embedding应该接近。

一、互联网中图结构数据

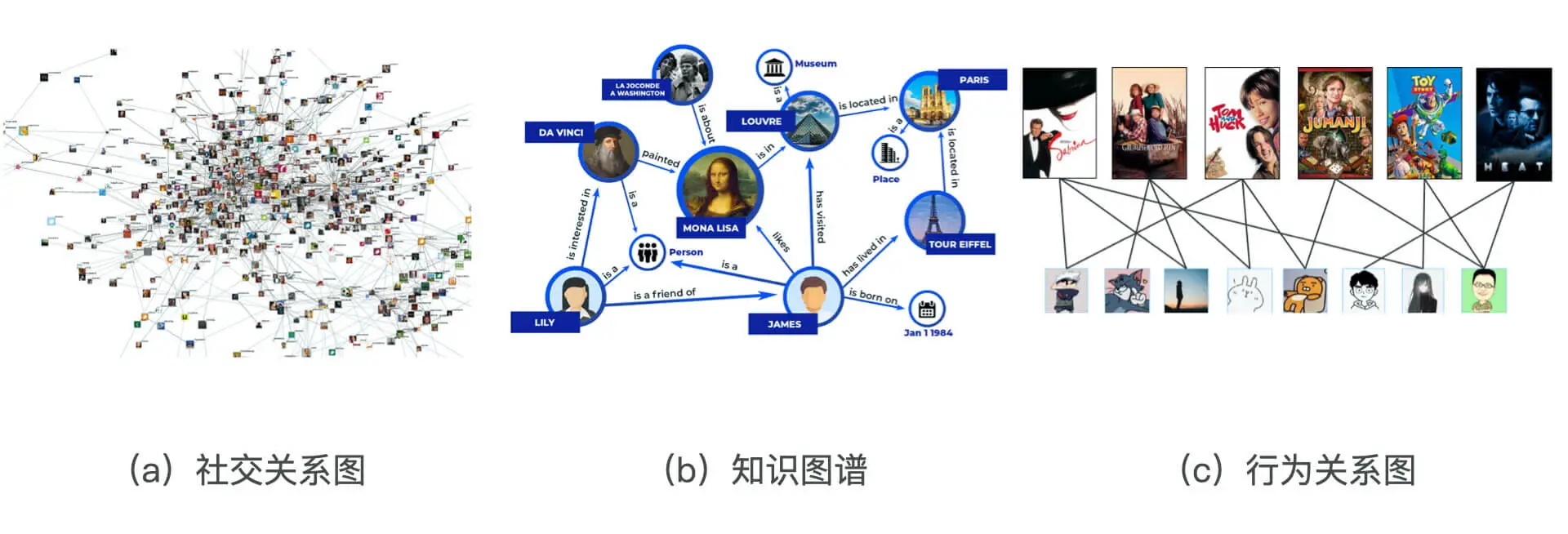
上个task中知道，只要是能够被序列数据表示的物品，都可以通过Item2vec训练出embedding，但是互联网中很多数据是以图数据展现（如下图）：

（1）社交网络。
社交网络中的节点进行embedding后能使社交化推荐更加方便；

（2）知识图谱。
包含不同类型的知识主体（如人物、地点等），附着在知识主体上的属性（如人物描述、物品特点）和主体之间、主体和属性之间的关系。我们可以对知识图谱中的主体进行embedding，从而发现主体之间的潜在关系。

（3）行为关系类型图数据。
这类数据几乎存在所有的互联网应用中，由用户和物品之间的相互行为组成的二部图（二分图）。可以通过embedding发物品物品之间、用户用户之间、用户和物品之间的关系。

二、基于随机游走的Graph Embedding：Deep Walk

2014年石溪大学提出的deep walk的主要思想：由物品组成的图结构上进行随机游走，从而产生的大量物品序列作为训练样本输入word2vec中训练，得到物品的embedding。
deepwalk可以被看作连接序列embedding和graph embedding之间的过渡方法。

2.1 Deep Walk算法过程

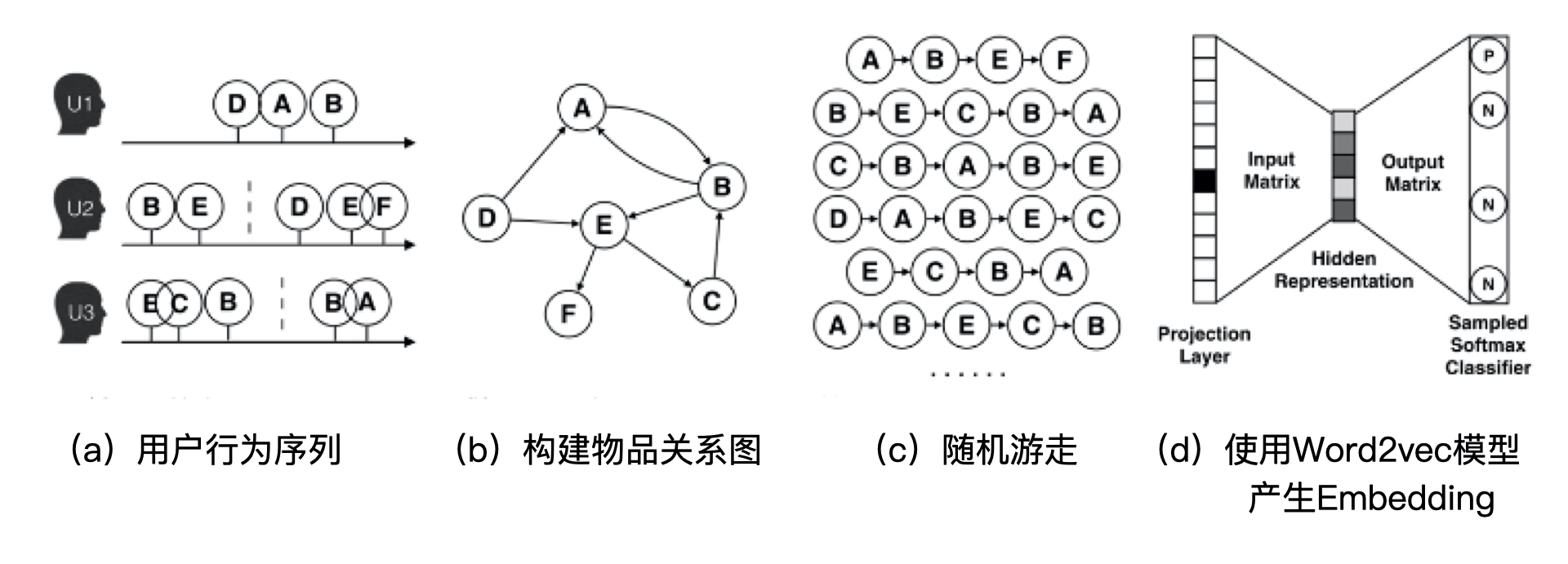
• 首先，我们基于原始的用户行为序列（图 2a），比如用户的购买物品序列、观看视频序列等等，来构建物品关系图（图 2b）。可以看出，因为用户 Ui先后购买了物品 A 和物品 B，所以产生了一条由 A 到 B 的有向边。如果后续产生了多条相同的有向边，则有向边的权重被加强。在将所有用户行为序列都转换成物品相关图中的边之后，全局的物品相关图就建立起来了。
• 然后，采用随机游走的方式随机选择起始点，重新产生物品序列（图 2c）。其中，随机游走采样的次数、长度等都属于超参数，需要根据具体应用进行调整。
• 最后，将这些随机游走生成的物品序列输入图 2d 的 Word2vec 模型，生成最终的物品 Embedding 向量。

2.2 随机游走的跳转概率

在上述 DeepWalk 的算法流程中，唯一需要形式化定义的就是随机游走的跳转概率，也就是到达节点 vi后，下一步遍历 vi 的邻接点 vj 的概率。如果物品关系图是有向有权图，那么从节点 vi 跳转到节点 vj 的概率定义如下：
P ( v j ∣ v i ) = { M i j ∑ j ∈ N + ( V i ) , m i j v j ∈ N + ( v i ) 0 , e i j ∉ ε P\left(v_{j} \mid v_{i}\right)=

• N+(vi) 是节点 vi所有的出边集合，Mij是节点 vi到节点 vj边的权重，即 DeepWalk 的跳转概率就是跳转边的权重占所有相关出边权重之和的比例。
• 如果物品相关图是无向无权重图，那么跳转概率将是上面这个公式的一个特例，即权重 Mij将为常数 1，且 N+(vi) 应是节点 vi所有“边”的集合，而不是所有“出边”的集合。

再通过随机游走得到新的物品序列，就可以通过经典的 Word2vec 的方式生成物品 Embedding 了。

三、在同质性和结构性间权衡：Node2vec

2016 年，斯坦福大学大佬在 DeepWalk 的基础上提出了 Node2vec 模型。Node2vec 通过调整随机游走跳转概率的方法，让 Graph Embedding 的结果在网络的同质性（Homophily）和结构性（Structural Equivalence）中进行权衡，可以进一步把不同的 Embedding 输入推荐模型，让推荐系统学习到不同的网络结构特点。

3.1 同质性和结构性

网络的“同质性”指的是距离相近节点的 Embedding 应该尽量近似，如图 3 所示，节点 u 与其相连的节点 s1、s2、s3、s4的 Embedding 表达应该是接近的，这就是网络“同质性”的体现。在电商网站中，同质性的物品很可能是同品类、同属性，或者经常被一同购买的物品。

“结构性”指的是结构上相似的节点的 Embedding 应该尽量接近，比如图 3 中节点 u 和节点 s6都是各自局域网络的中心节点，它们在结构上相似，所以它们的 Embedding 表达也应该近似，这就是“结构性”的体现。在电商网站中，结构性相似的物品一般是各品类的爆款、最佳凑单商品等拥有类似趋势或者结构性属性的物品。

3.2 如何表达结构性和同质性

Graph Embedding 的结果究竟是怎么表达结构性和同质性的呢？

• 首先，为了使 Graph Embedding 的结果能够表达网络的“结构性”，在随机游走的过程中，我们需要让游走的过程更倾向于 BFS（Breadth First Search，宽度优先搜索），因为 BFS 会更多地在当前节点的邻域中进行游走遍历，相当于对当前节点周边的网络结构进行一次“微观扫描”。（当前节点是“局部中心节点”，还是“边缘节点”，亦或是“连接性节点”，其生成的序列包含的节点数量和顺序必然是不同的，从而让最终的 Embedding 抓取到更多结构性信息。）

• 而为了表达“同质性”，随机游走要更倾向于 DFS（Depth First Search，深度优先搜索）才行，因为 DFS 更有可能通过多次跳转，游走到远方的节点上。但无论怎样，DFS 的游走更大概率会在一个大的集团内部进行，这就使得一个集团或者社区内部节点的 Embedding 更为相似，从而更多地表达网络的“同质性”。

那在 Node2vec 算法中，究竟是怎样控制 BFS 和 DFS 的倾向性的呢？

• 其实，它主要是通过节点间的跳转概率来控制跳转的倾向性。图 4 所示为 Node2vec 算法从节点 t 跳转到节点 v 后，再从节点 v 跳转到周围各点的跳转概率。这里，你要注意这几个节点的特点。比如，节点 t 是随机游走上一步访问的节点，节点 v 是当前访问的节点，节点 x1、x2、x3是与 v 相连的非 t 节点，但节点 x1还与节点 t 相连，这些不同的特点决定了随机游走时下一次跳转的概率。

这些概率还可以用具体的公式来表示，从当前节点 v 跳转到下一个节点 x 的概率$${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot {\omega }_{vx}$$其中 Wvx 是边 vx 的原始权重，${\alpha }_{pq}(t,x)$ 是 Node2vec 定义的一个跳转权重。到底是倾向于 DFS 还是 BFS，主要就与这个跳转权重的定义有关了：

α p q ( t , x ) = { 1 p  如果  d t x = 0 1  如果  d t x = 1 1 q  如果  d t x = 2 \alpha_{p q(t, x)=}

${\alpha }_{pq}(t,x)$里的$d_{tx}$ 是指节点 t 到节点 x 的距离，比如节点 x1其实是与节点 t 直接相连的，所以这个距离 $d_{tx}$就是 1，节点 t 到节点 t 自己的距离 $d_{tt}$就是 0，而 x2、x3这些不与 t 相连的节点，$d_{tx}$就是 2。

此外，${\alpha }_{pq}(t,x)$ 中的参数 p 和 q 共同控制着随机游走的倾向性。参数 p 被称为返回参数（Return Parameter），p 越小，随机游走回节点 t 的可能性越大，Node2vec 就更注重表达网络的结构性。参数 q 被称为进出参数（In-out Parameter），q 越小，随机游走到远方节点的可能性越大，Node2vec 更注重表达网络的同质性。

反之，当前节点更可能在附近节点游走。可以自己尝试给 p 和 q 设置不同大小的值，算一算从 v 跳转到 t、x1、x2和 x3的跳转概率。这样应该就能理解刚才所说的随机游走倾向性的问题啦。

3.3 实验证实

Node2vec 这种灵活表达同质性和结构性的特点也得到了实验的证实，可以通过调整 p 和 q 参数让它产生不同的 Embedding 结果。
图 5 上就是 Node2vec 更注重同质性的体现，从中可以看到，距离相近的节点颜色更为接近，图 5 下则是更注重结构性的体现，其中结构特点相近的节点的颜色更为接近。

Node2vec 所体现的网络的同质性和结构性，在推荐系统中都是非常重要的特征表达。由于 Node2vec 的这种灵活性，以及发掘不同图特征的能力，可以把不同 Node2vec 生成的偏向“结构性”的 Embedding 结果，以及偏向“同质性”的 Embedding 结果共同输入后续深度学习网络，以保留物品的不同图特征信息。

四、Embedding在推荐系统的应用

embedding产生的是一个数值型特征向量，即embedding可以看做在处理特征，但是和one-hot编码等方式不同，embedding的更高阶性体现在：把序列结构、网络结构、甚至其他特征融合到一个特征向量中。

embedding在推荐系统的特征工程上的应用：

• 【直接应用】直接利用得到的embedding向量的相似性进行推荐系统的某些功能：如实现相似物品推荐，利用物品embedding和用户embedding的相似性实现“猜你喜欢”等推荐功能；利用物品embedding实现推荐系统中的召回层。
• 【预训练应用】预训练好物品和用户的embedding后并没直接应用，而是将其作为特征向量的一部分，和其他特征向量拼接起来以作为推荐模型的input——这样能更好的把其他特征引入，从而推荐系统的预测更全面准确。
• 【End2End应用】端到端训练。不预先训练embedding，把embedding的训练和推荐模型结合，采用统一的、端到端的方式一起训练，直接得到包含embedding层的推荐模型。

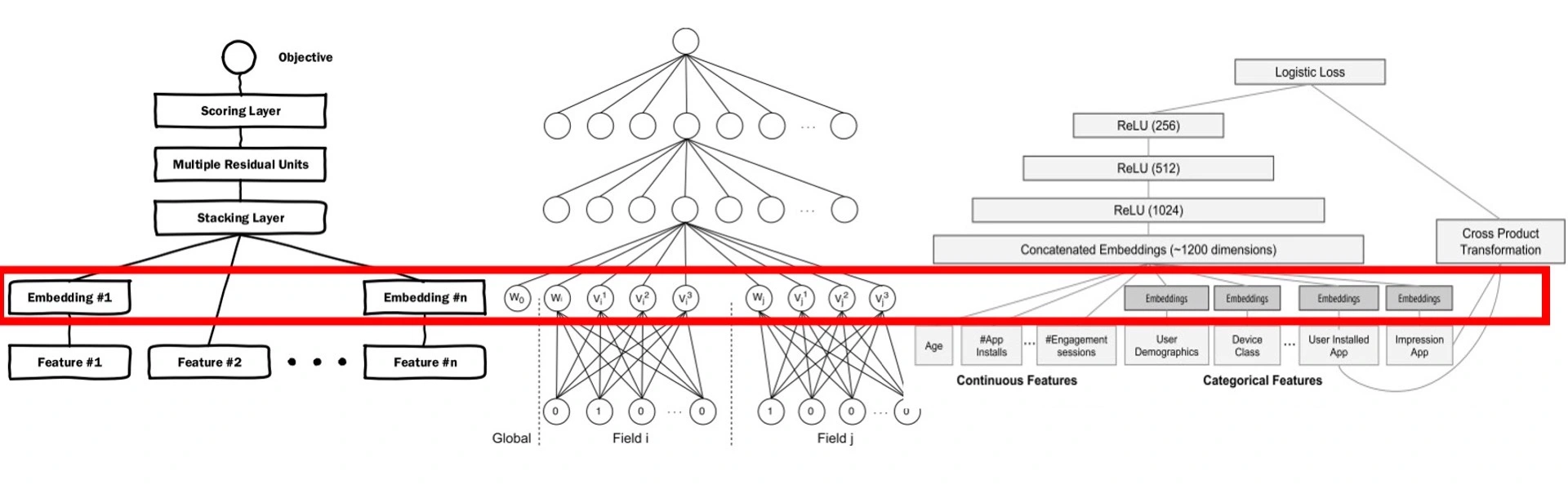
微软的Deep Crossing，UCL提出的FNN和Google的Wide&Deep都是第三种。

五、作业

对比一下 Embedding 预训练和 Embedding End2End 训练这两种应用方法，它们之间的优缺点？

Embedding预训练的优点：
1.更快。因为对于End2End的方式，Embedding层的优化还受推荐算法的影响，这会增加计算量。
2.难收敛。推荐算法是以Embedding为前提的，在端到端的方式中，在训练初期由于Embedding层的结果没有意义，所以推荐模块的优化也可能不太有意义，可能无法有效收敛。

Embedding端到端的优点：可能收敛到更好的结果。端到端因为将Embedding和推荐算法连接起来训练，那么Embedding层可以学习到最有利于推荐目标的Embedding结果。

六、课后答疑

（1）“首先，为了使 Graph Embedding 的结果能够表达网络的“结构性”，在随机游走的过程中，我们需要让游走的过程更倾向于 BFS（Breadth First Search，宽度优先搜索）”
这里应该是DFS吧？并且同质性是使用BFS？

可以推荐参考原文中的解释。
We observe that BFS and DFS strategies play a key role in producing representations that reflect either of the above equivalences.
In particular, the neighborhoods sampled by BFS lead to embeddings that correspond closely to structural equivalence.
The opposite is true for DFS which can explore larger parts of the network as it can move further away from the source node u (with sample size k being fixed).
In DFS, the sampled nodes more accurately reflect a macro-view of the neighborhood which is essential in inferring communities based on homophily.

参考译文：我们观察到，BFS 和 DFS 策略在产生向量表达时发挥着关键的作用。特别是通过 BFS 采样得到的邻域节点使生成的相应 Embedding 更接近结构性一致。而对于 DFS 来说，情况恰恰相反，由于 DFS 可以进一步采样到远离节点 u（样本大小 k 固定）的部分，因此可以探索更大范围的网络。在 DFS 中，采样的节点可以更准确地反映邻域的宏观视图，这对于推断社区的同质性至关重要。

原文地址 https://github.com/wzhe06/Reco-papers/blob/master/Embedding/%5BNode2vec%5D%20Node2vec%20-%20Scalable%20Feature%20Learning%20for%20Networks%20%28Stanford%202016%29.pdf

Reference

（1）https://github.com/wzhe06/Reco-papers
（2）《深度学习推荐系统实战》，王喆

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/120838642