自动控制原理三:控制系统时域分析法
3.3 二阶系统时域分析
定义:由二阶微分方程描述的系统称为二阶系统 . 它在控制工程中的应用极为广泛 . 许多高阶系统在一定的条件下 , 也可简化为二阶系统来研究 .
典型二阶系统的微分方程:
T 2 d 2 c ( t ) d t 2 + 2 ζ T d c ( t ) d t + c ( t ) = r ( t ) , t ≥ 0 T^{2} \frac{d^{2}c(t)}{dt^{2}}+2 \zeta T \frac{dc(t)}{dt}+c(t)=r(t), t ≥ 0 T2dt2d2c(t)+2ζTdtdc(t)+c(t)=r(t),t≥0
其数学模型图如下:

开环传递函数为 :
G ( s ) = ω n 2 s 2 + 2 ζ ω n s G(s)= \frac{ \omega _{n}^{2}}{s^{2}+2 \zeta \omega _{n}s} G(s)=s2+2ζωnsωn2
闭环传递函数为 :
Φ ( s ) = G ( s ) 1 + G ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 \Phi (s)= \frac{G(s)}{1+G(s)}= \frac{ \omega _{n}^{2}}{s^{2}+2 \zeta \omega _{n}s+ \omega _{n}^{2}} Φ(s)=1+G(s)G(s)=s2+2ζωns+ωn2ωn2
瞬态响应指标:
- 通常要求系统的瞬态响应既具有充分的快速性 , 又具有足够的阻尼 .
- 为了获得满意的二阶系统瞬态响应特性 , 阻尼比必须选择在 0 . 4 ~ 0 . 8 之间 ( 小于 0 . 4 的值会造成系统瞬态响应严重过调 , 大于 0 . 8 则会导致系统响应变得缓慢 ) .(处于欠阻尼)
- (平稳性 VS 快速性 ) 最大超调量和上升时间是相互矛盾的 ,最大超调量和上升时间两者不可能同时都达到比较小的数值 , 如果其中一个比较小 , 那么另一个必然比较大 .(寻找最优解)
- 动态性能和稳态误差相互矛盾 ( 与开环增益 K 有关 ) .
关系式为:(LPLS终值定理)
e s s = lim s → 0 s E ( s ) = lim s → 0 s × s ( s + 2 ζ ω n ) s 2 + 2 ζ ω n s + ω n 2 × 1 s 2 = 2 ζ ω n e_{ss}= \lim _{s \rightarrow 0}sE(s)= \lim _{s \rightarrow 0}s \times \frac{s(s+2 \zeta \omega _{n})}{s^{2}+2 \zeta \omega _{n}s+ \omega _{n}^{2}} \times \frac{1}{s^{2}}= \frac{2 \zeta }{ \omega _{n}} ess=s→0limsE(s)=s→0lims×s2+2ζωns+ωn2s(s+2ζωn)×s21=ωn2ζ
改善二阶系统响应特性措施:
为了改善系统性能而改变系统的结构、参数或附加具有一定功能的环节的方法称为对系统进行校正 . 附加环节称为校正环节 , 比例微分控制和速度反馈是较常用的校正方法
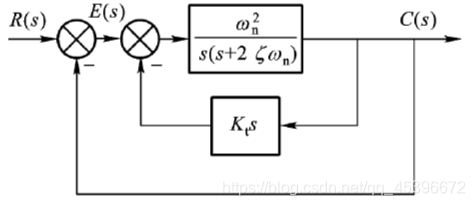
- 输出量的速度反馈控制:
将输出量的速度信号 c ’ ( t ) 采用负反馈形式反馈到输入端并与误差信号 e ( t ) 比较 , 构成一个内反馈回路 , 简称速度反馈

闭环传递函数:
Φ ( s ) = C ( s ) R ( s ) = ω n 2 s 2 + ( 2 ζ ω n + K t ω n 2 ) s + ω n 2 \Phi (s)= \frac{C(s)}{R(s)}= \frac{ \omega _{n}^{2}}{s^{2}+(2 \zeta \omega _{n}+K_{t} \omega _{n}^{2})s+ \omega _{n}^{2}} Φ(s)=R(s)C(s)=s2+(2ζωn+Ktωn2)s+ωn2ωn2
等效阻尼比 :
ζ t = ζ + 1 2 K t ω n \zeta _{t}= \zeta + \frac{1}{2}K_{t} \omega _{n} ζt=ζ+21Ktωn
对比原来阻尼比,等效阻尼比增大了 , 振荡倾向和超调量减小 , 改善了系统的平稳性 . - 误差的比例 - 微分控制:
以误差信号 e ( t ) 与误差信号的微分信号 e ’ ( t) 的和产生控制作用 . 简称 PD控制

系统开环传递函数为 :
G ( s ) = C ( s ) E ( s ) = ω n 2 ( 1 + T d S ) s ( s + 2 ζ ω m ) G(s)= \frac{C(s)}{E(s)}= \frac{ \omega _{n}^{2}(1+T_{d}S)}{s(s+2 \zeta \omega _{m})} G(s)=E(s)C(s)=s(s+2ζωm)ωn2(1+TdS)
闭环传递函数为 :
Φ ( s ) = C ( s ) R ( s ) = ω n 2 ( 1 + T d s ) s 2 + ( 2 ζ ω n + T d ω n 2 ) s + ω n 2 \Phi (s)= \frac{C(s)}{R(s)}= \frac{ \omega _{n}^{2}(1+T_{d}s)}{s^{2}+(2 \zeta \omega _{n}+T_{d} \omega _{n}^{2})s+ \omega _{n}^{2}} Φ(s)=R(s)C(s)=s2+(2ζωn+Tdωn2)s+ωn2ωn2(1+Tds)
等效阻尼比 :
ζ d = ζ + 1 2 T d ω n \zeta_{d} = \zeta + \frac{1}{2}T_{d} \omega_{n} ζd=ζ+21Tdωn
- 引入了比例一微分控制 , 使系统的等效阻尼比加大了 , 从而 抑制了振荡 , 使超调减弱 , 可以改善系统的平稳性 .
- 微分作用之所以能改善动态性能 , 因为它产生一种早期控制 (或称为超前控制 ) , 能在实际超调量出来之前 , 就产生一个修正作用 .
比例-微分控制等效图:
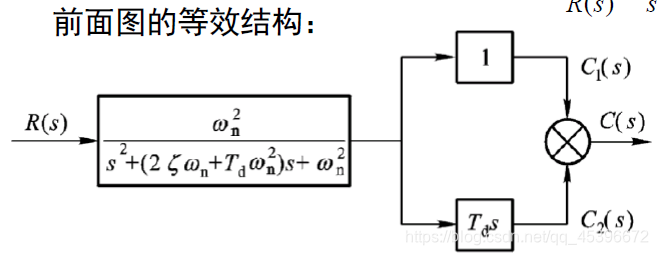
即由原输出上叠加一个超前量;图示
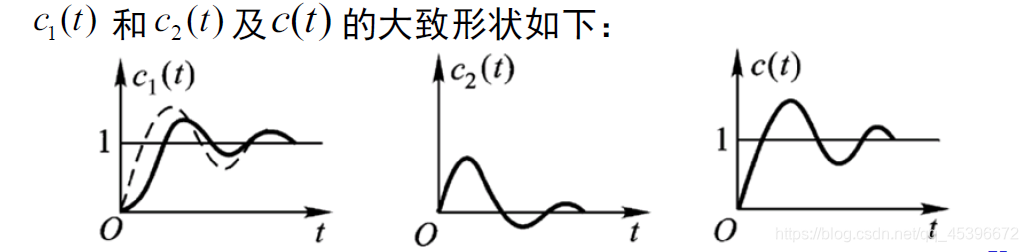
由等效阻尼比可以推算得到:
增加 T _a 项 , 增大了等效阻尼比 ζ _a , 使 c _1 ( t ) 曲线比较平稳 . 另一方面 , 它又使 c 1 ( t ) 加上了它的微分信号 c 2 ( t ) ,加速了 c ( t ) 的响应速度 , 但同时削弱了等效阻尼比 ζ d 的平稳作用 .
总结 :
引入误差信号的比例一微分控制 , 能否真正改善二阶系统的响应特性 , 还需要适当选择微分时间常数 T . 若大一些 , 使 c 1 ( t ) 具有过阻尼的形式 , 而闭环零点的微分作用 , 将在保证响应特性平稳的情况下 , 显著地提高系统的快速性 .
- 两者的比较:
从实现角度看 :比例一微分控制的线路结构比较简单 , 成本低 ; 而速度反馈控制部件则较昂贵 .
从抗干扰来看 :前者抗干扰能力较后者差 .
从控制性能看 :两者均能改善系统的平稳性 , 在相同的阻尼比和自然频率下 , 采用速度反馈不足之处是其会使系统的
开环增益下降 , 但又能使内回路中被包围部件的非线性特性、参数漂移等不利影响大大削弱 .
3.4高阶系统的时域分析
3.4.1高阶系统的时域响应
高阶系统的传递函数为:
Φ ( s ) = C ( s ) R ( s ) = b 0 s m + b 1 s m − 1 + ⋯ b m − 1 s + b m a 0 s n + a 1 s n − 1 + ⋯ + a n − 1 s + a n , n ⩾ m \Phi (s) =\frac{C(s)}{R(s)}= \frac{b_{0}s^{m}+b_{1}s^{m-1}+ \cdots b_{m-1}s+b_{m}}{a_{0}s^{n}+a_{1}s^{n-1}+ \cdots +a_{n-1}s+a_{n}},n \geqslant m Φ(s)=R(s)C(s)=a0sn+a1sn−1+⋯+an−1s+anb0sm+b1sm−1+⋯bm−1s+bm,n⩾m
= K ( s + z 1 ) ( s + z 2 ) ⋯ ( s + z m ) ( s + p 1 ) ( s + p 2 ) ⋯ ( s + p m ) , n ⩾ m = \frac{K(s+z_{1})(s+z_{2}) \cdots (s+z_{m})}{(s+p_{1})(s+p_{2}) \cdots (s+p_{m})},n \geqslant m =(s+p1)(s+p2)⋯(s+pm)K(s+z1)(s+z2)⋯(s+zm),n⩾m
零极点的另一种形式:

其单位阶跃响应函数为:

高阶系统的单位阶跃响应取决于闭环系统的零 、极点分布 .
定性分析:
对于闭环极点全部位于 s 左半平面的高阶系统 ( 否则系统不稳定 ) , 极点为实数 ( 指数衰减项 ) 和共轭复数 ( 衰减正弦项 )的衰减快慢取决于极点离虚轴的距离 . 远 , 衰减的快 ; 近 , 衰减的慢 . 所以 , 近极点对瞬态响应影响大 .
系数 aj βl Yl 取决于零、极点分布 . 有以下几种情况 :
若极点远离原点 , 则系数小 ;
极点靠近一个零点 , 远离其他极点和零点 , 系数小 ;
极点远离零点 , 又接近原点或其他极点 , 系数大 .
衰减慢且系数大的项在瞬态过程中起主导作用 .
[主导极点 ] : 满足下列条件的极点称为主导极点 .
系统中有一实数极点 ( 或一对复数极点 ) 距虚轴最近 ;
附近无闭环零点 ;
其他闭环极点距虚轴的距离是它的 5 倍以上 .
主导极点在 c ( t ) 中的对应项衰减最慢 , 系数最大 , 系统的瞬态性能指标主要由它决定 , 体现其主导作用 . 具有主导极点的高阶系统**可近似为二阶系统 .**利用主导极点的概念可以对高阶系统的特性做近似的估计分析 .高阶系统近似简化原则 :
在近似前后 , 确保输出稳态值不变 ;
在近似前后 , 瞬态过程基本相差不大 .
[偶极子 ] : 如果闭环系统的一个零点与一个极点彼此十分靠近 , 常称这样的闭环零、极点为偶极子 . 只要偶极子不十分靠近坐极原点 , 则它对系统瞬态响应的影响就很小 , 因而可忽略它们的存在 . 但影响稳态性能 .
文章来源: blog.csdn.net,作者:JeckXu666,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_45396672/article/details/109479161
- 点赞
- 收藏
- 关注作者



评论(0)