📢📢📢📣📣📣
🌻🌻🌻Hello，大家好我叫是Dream呀，一个有趣的Python博主，小白一枚，多多关照😜😜😜
🏅🏅🏅CSDN Python领域新星创作者，大二在读，欢迎大家找我合作学习
💕入门须知：这片乐园从不缺乏天才，努力才是你的最终入场券！🚀🚀🚀
💓最后，愿我们都能在看不到的地方闪闪发光，一起加油进步🍺🍺🍺
🍉🍉🍉“一万次悲伤，依然会有Dream，我一直在最温暖的地方等你”，唱的就是我！哈哈哈~🌈🌈🌈
🌟🌟🌟✨✨✨

@TOC

4.1分而治之

下面我们将探索分而治之——一种著名的递归式问题解决方法。
快速排序是一种排序算法，速度比第二章介绍的选择排序快得多，实属优雅代码的典范。
使用递归函数步骤：
1.找出基线条件
2.每次递归调用都必须离空数组更进一步。
即：缩小问题规模！

编写涉及数组的递归函数条件时，基线条件通常是数组为空或者只包含一个元素。陷入困境时，应该先检查基线条件是不是这样的。

4.2快速排序

快速排序是一种常用的排序算法，比选择排序快得多！
首先，从数组中选择一个元素，这个元素被称为基准值。
然后，找出比基准值小的元素以及比基准值大的元素。
这被称为分区，现在你有：

1. 一个由小于基准值的数字组成的子数组；
2. 基准值；
3. 一个由所有大于基准值的数字助组成的子数组。
   这里进行了分区，得到的两个子数组都是无序的。但如果这两个数组是无序的，对整个数组进行排序将非常容易。

排序步骤：
1.选择基准值；
2.将数组分成两个子数组：小于基准值的元素组成的子数组和大于基准值的元素组成的子数组。
3.对这两个子数组进行快速排序。

# -*-coding:utf-8 -*-
# @Author:到点了,心疼徐哥哥
# 奥利给干！！！
def quicksort(array):
    if len(array)<2:
        return array
    else:
        pivot=array[0]
        less=[i for i in array[1:] if i <= pivot]
        greater=[i for i in array[1:] if i > pivot]
        return quicksort(less)+[pivot]+quicksort(greater)
print(quicksort([2,6,5,3,9]))

4.3再谈大O表示法

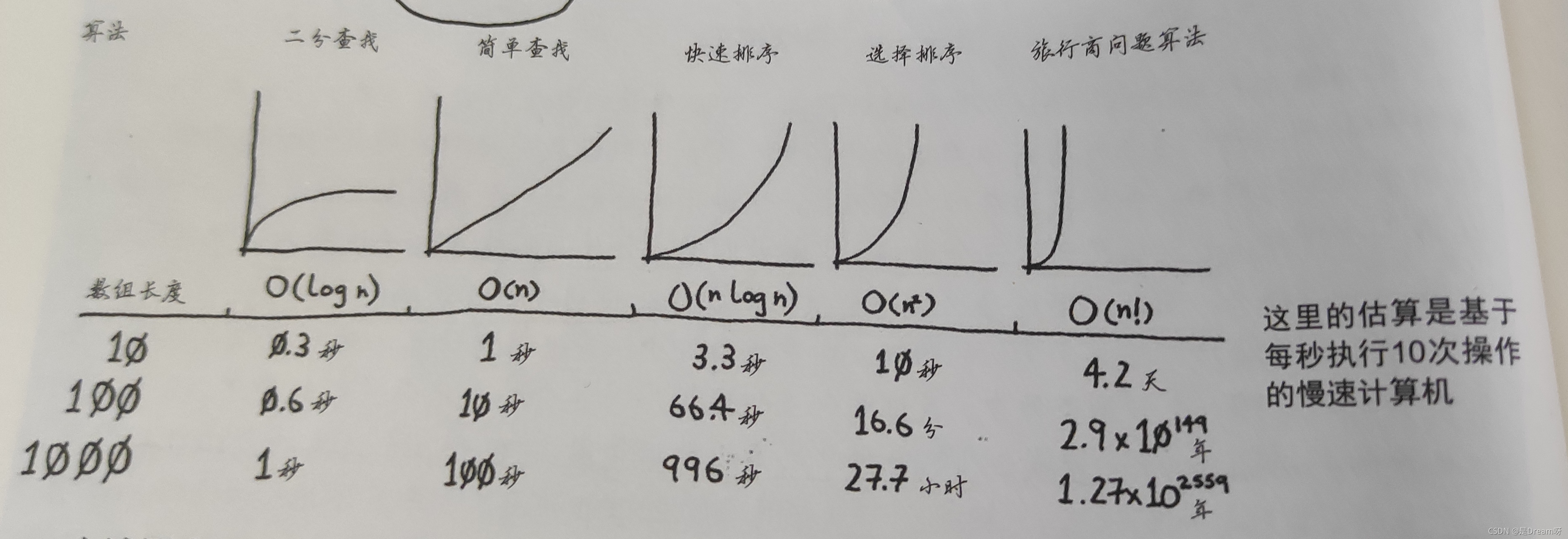
这些数据并不准确，这里提供他们的时间只是想让你对时间的差别有大致的认识，实际上，计算机每秒的执行的操作远不止10次。
还有一种名为合并排序的排序算法，其运行时间为O（nlog n），比选择排序快得多！快速排序的情况比较棘手，在最糟糕的情况下，其运行时间为O（n**2）。

4.4总结

1.D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或者只包含一个元素的数组。
2.实现快速排序时，请随机选择用作基准值的元素。快速排序的平均运行时间O（nlog n）。
3.大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
4.比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O（log n）的速度比O（n）快得多！

🌲🌲🌲 好啦，这就是今天要分享给大家的全部内容了
❤️❤️❤️如果你喜欢的话，就不要吝惜你的一键三连了~