跟着动画学Go数据结构之堆排序

堆排序

堆排序是一种树形选择排序算法。

简单选择排序算法每次选择一个关键字最小的记录需要 O(n) 的时间，而堆排序选择一个关键字最小的记录需要 O(nlogn) 的时间。

堆可以看作一棵完全二叉树的顺序存储结构。

在这棵完全二叉树中，如果每个节点的值都大于等于左边孩子的值，称为大根堆（最大堆、又叫大顶堆）。如果每个节点的值都小于等于左边孩子的值，称为小根堆（最小堆，小顶堆）。

可以，用数学符号表示如下：

大顶堆满足：k_i >= k_{2i} 且 k_i >= k_{2i+1}

小顶堆满足：k_i <= k_{2i} 且 k_i <= k_{2i+1}

父节点序号：(i-1)/2

左孩子序号：2i+1

右孩子：2i+2

堆排序过程

1. 构建初始堆

2. 在输出堆的顶层元素后，从上到下进行调整，将顶层元素与其左右子树的根节点进行比较，并将最小的元素交换到堆的顶部；然后不断调整直到叶子节点得到新的堆。

假如，​​{1, 7, 9, 2, 4, 6, 3, 5, 8}​​ 建堆，然后进行堆排序输出。

动画显示

1. 初始化堆，建堆操作图画演示：

首先根据无序序列 ​​{1, 7, 9, 2, 4, 6, 3, 5, 8}​​ 按照完全二叉树的顺序构建一棵完全二叉树，如图：

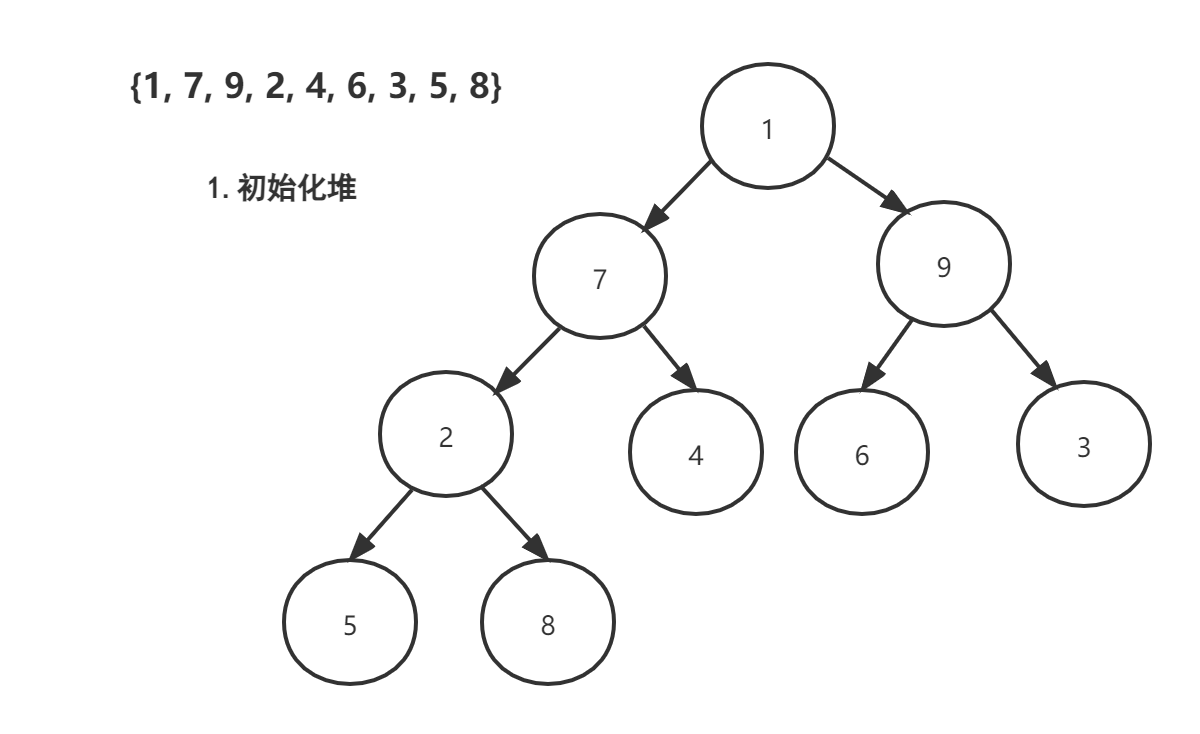
然后从最后一个分支节点 n/2开始调整堆，这里 9 / 2 = 4:

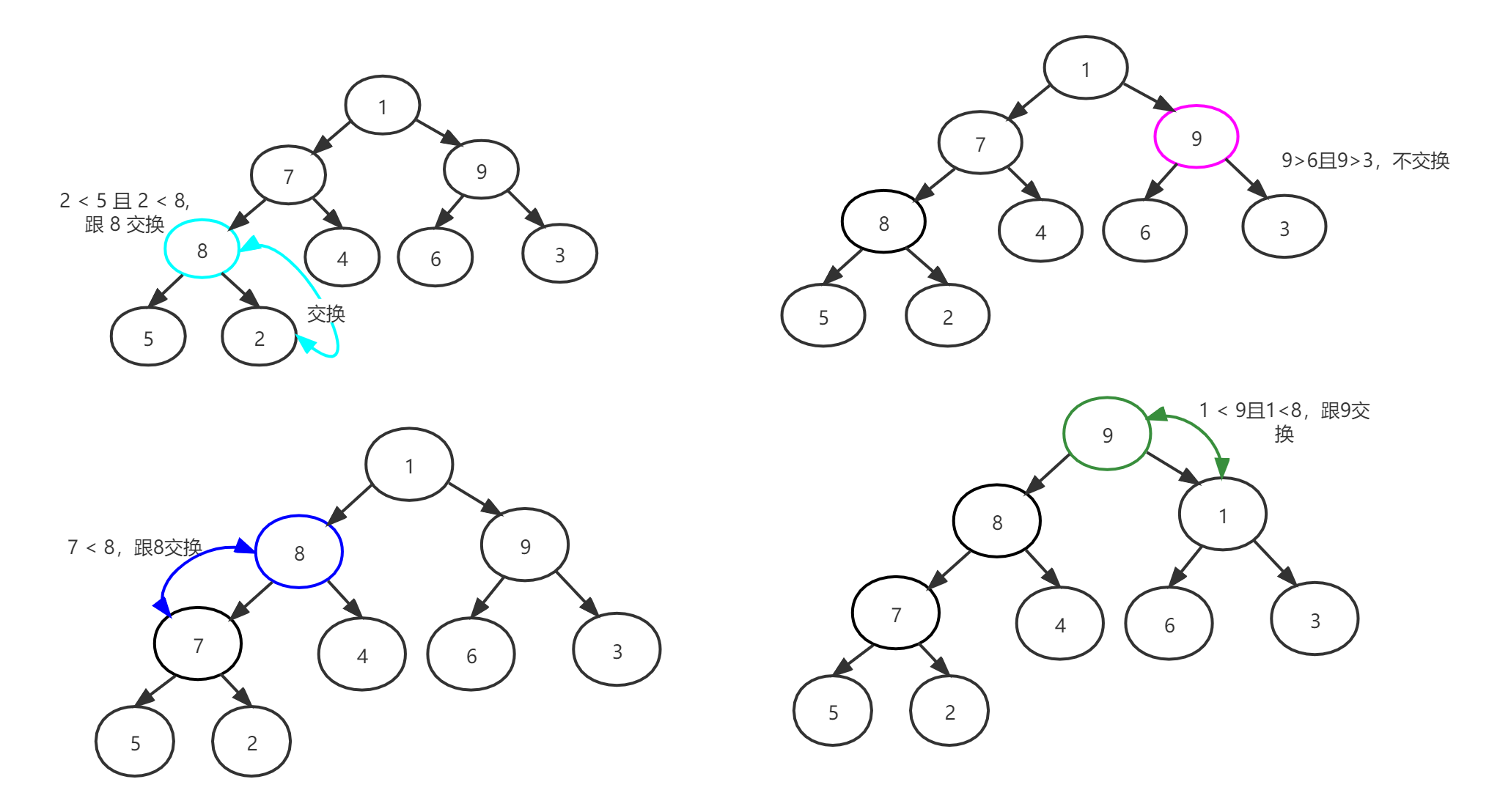
然后从 n/2-1 开始调整，即序号 3 开始调整，接着从 n/2-2 执行调整操作，如图所示：

一直重复到序号为 1 的节点：

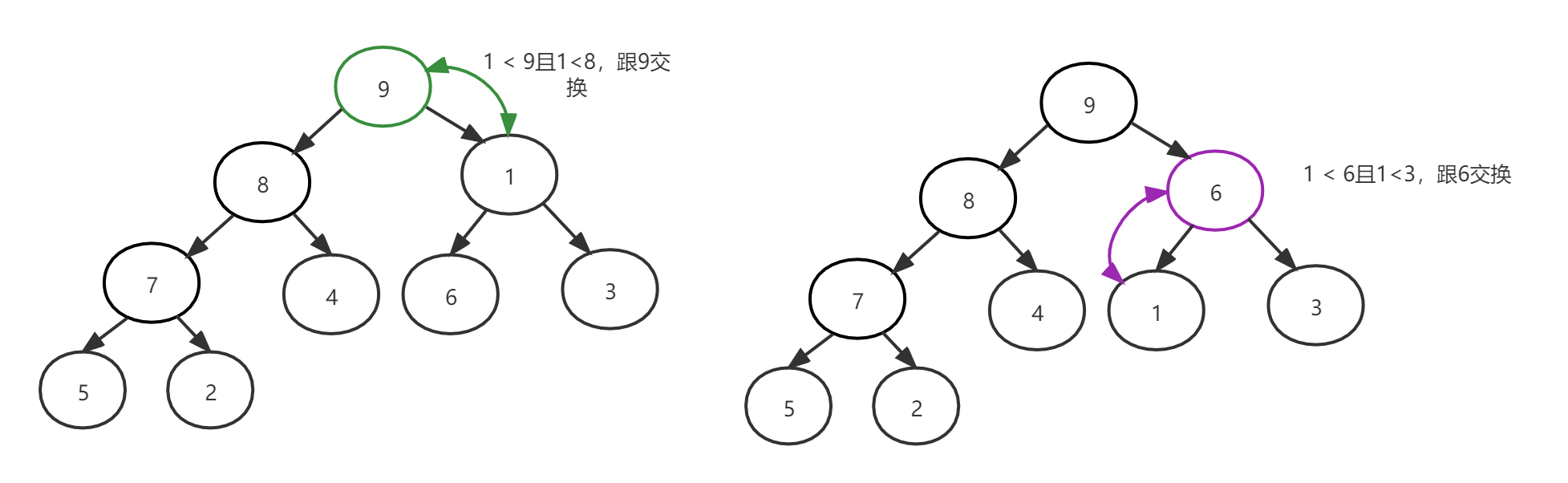
最终通过此次调整堆，得到新的堆为 ​​[9, 8, 6, 7, 4, 1, 3, 5, 2]​​ ，得到新的堆后开始堆排序过程

1. 开始堆排序

构建完初始堆后，此时，我们可以进入堆排序，从上面的方法中，

我们可以已知我们构建的最大堆的堆顶是最大的记录，可以可以将堆顶交换到最后一个元素的位置，然后执行堆顶下沉操作，然后再执行堆调整操作（新的堆顶也是最大值），直到剩余一个节点，得到一个有序序列。

此时，我们又可以进行堆调整操作，如下图：

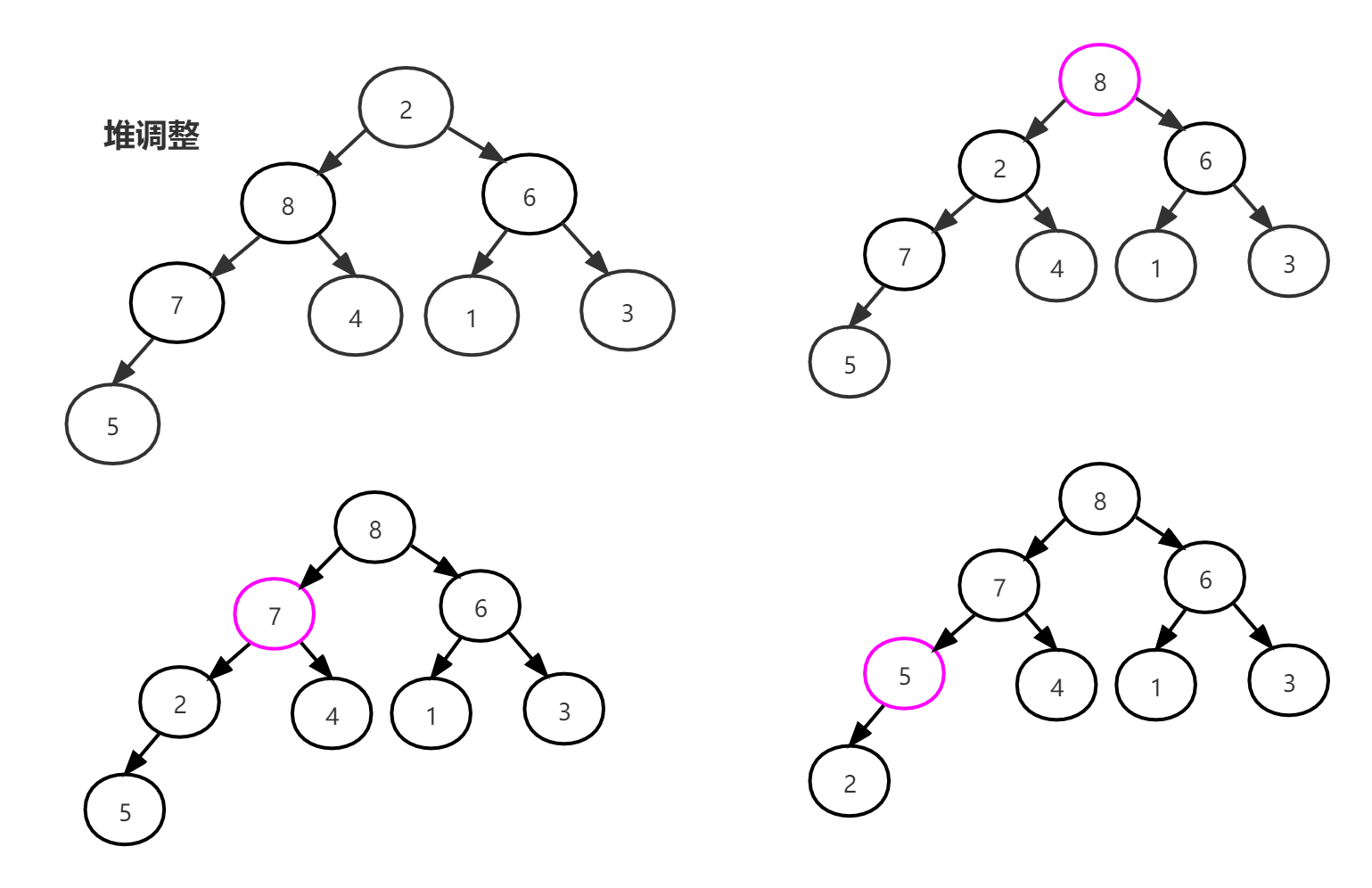
堆调整完毕，开始把新的堆顶 8 和最后一个记录 2 进行交换，然后将堆顶下沉，调整为堆，如下图所示：

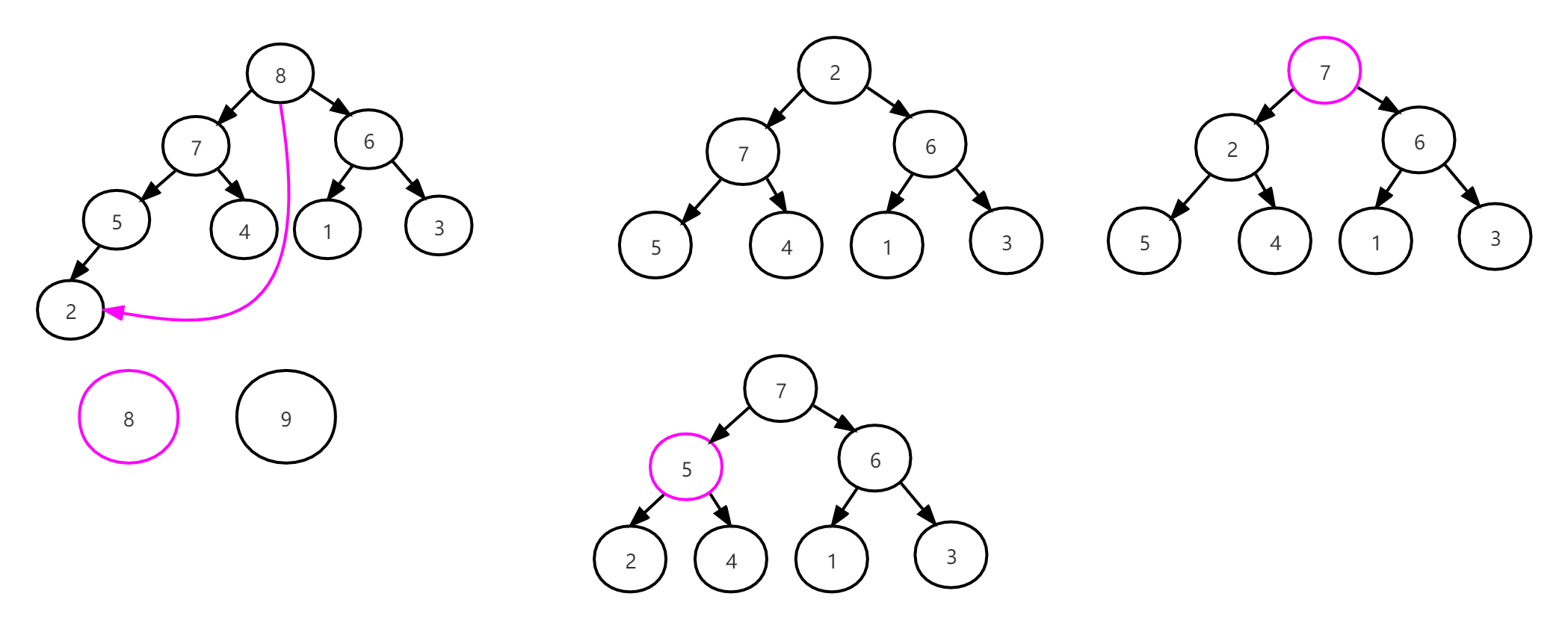
从此我们得到新的堆顶 7 ，然后把 7 跟最后一个元素 3 进行交换，7 下沉，然后堆调整，慢慢得到堆顶 6 和 堆顶5，如图所示：

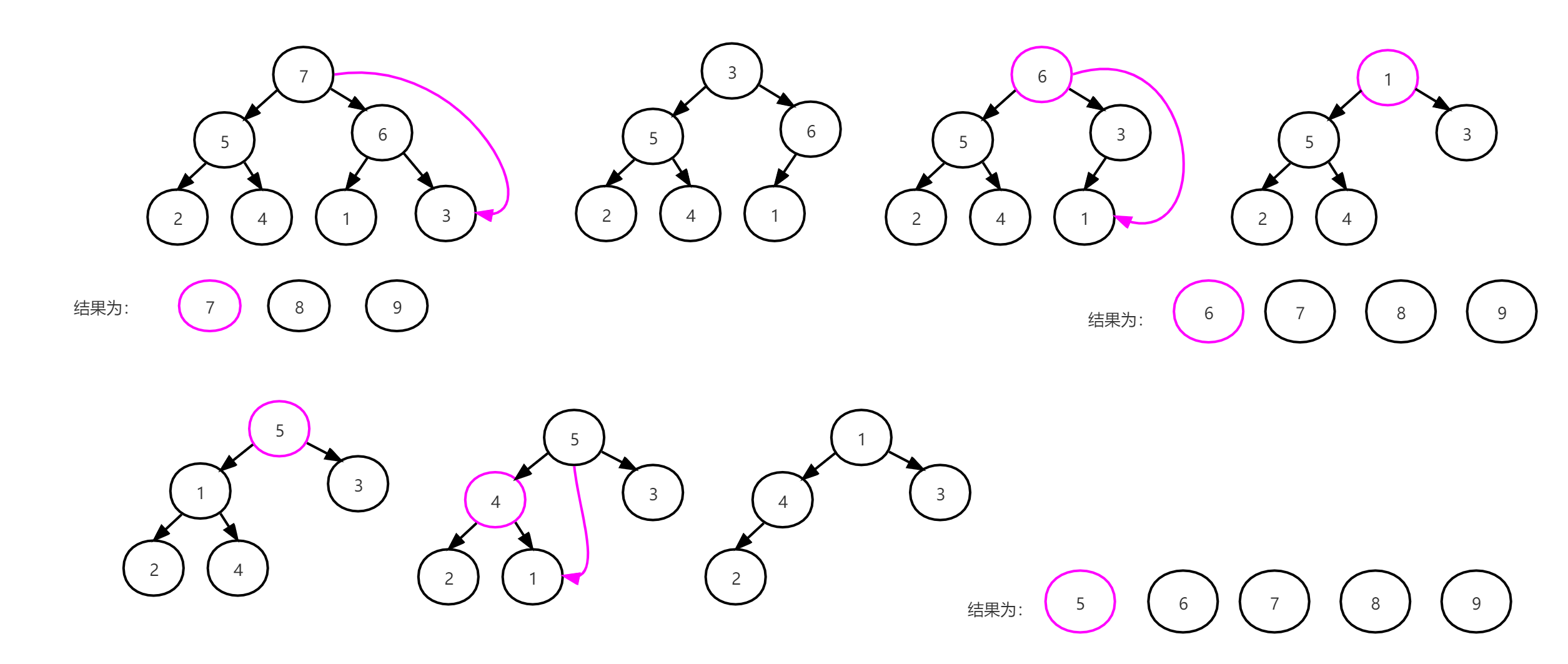
然后是 3 下沉：

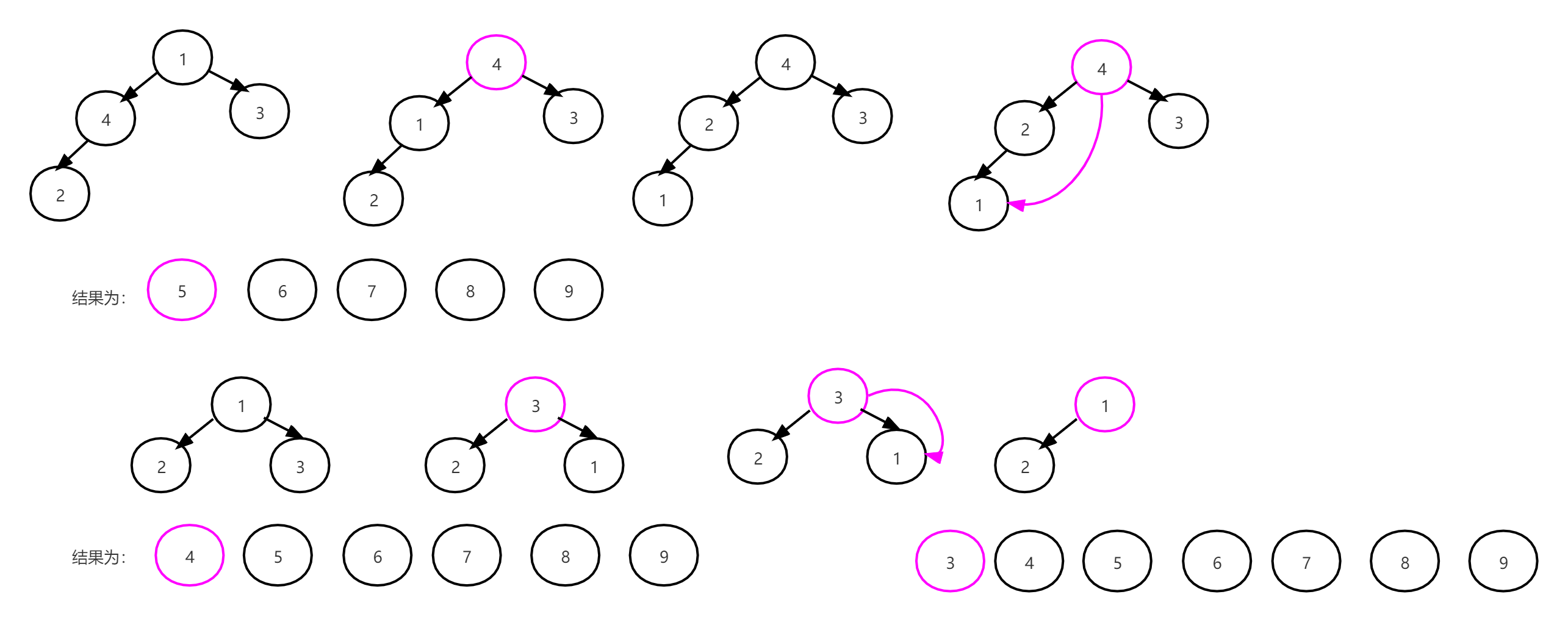
最后，堆顶 2 与最后一个记录 1 进行交换，只剩一个节点，堆排序结束，如下图所示：

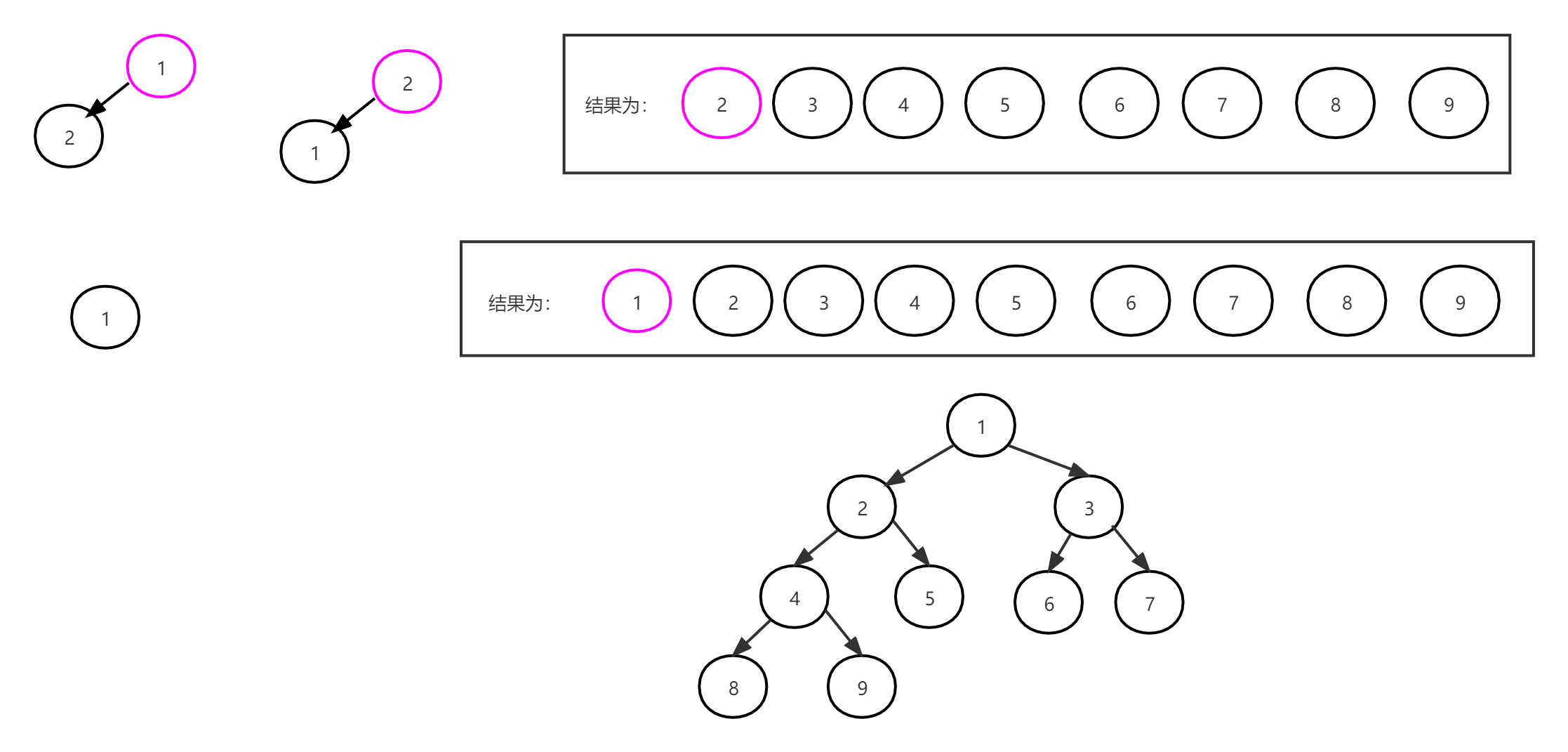
我们得到的新的序列按序号读取数据，就是一个有序序列。

代码实现

最后，我们用代码来检验一下我们的动画过程是否正确，如下：

package main
import "fmt"
// 调整堆
func adjustHeap(array []int, currentIndex int, maxLength int) {
    var noLeafValue = array[currentIndex] // 当前非叶子节点
    // j 指向左孩子
    // 当前非叶子节点的左节点为：2 * currentIndex + 1
    for j := 2*currentIndex + 1; j <= maxLength; j = currentIndex*2 + 1 {
        if j < maxLength && array[j] < array[j+1] { // 如果有右孩子，且左孩子比右孩子小
            j++ // j 指向右孩子
        }
        if noLeafValue >= array[j] {
            break // 非叶子节点大于孩子节点，跳过不交换
        }
        array[currentIndex] = array[j] // 移动到当前节点的父节点
        currentIndex = j               // j 指向交换后的新位置，继续向下比较
    }
    array[currentIndex] = noLeafValue // 放在合适的位置
}
// 初始化堆
func createHeap(array []int, length int) {
    // 建堆
    for i := length / 2; i >= 0; i-- {
        adjustHeap(array, i, length-1)
    }
}
func heapSort(array []int, length int) {
    for i := length - 1; i > 0; i-- {
        array[0], array[i] = array[i], array[0]
        adjustHeap(array, 0, i-1)
    }
}
func main() {
    var unsorted = []int{1, 7, 9, 2, 4, 6, 3, 5, 8}
    var length = len(unsorted)
    fmt.Println("建堆之前：")
    for i := 0; i < length; i++ {
        fmt.Printf("%d,", unsorted[i])
    }
    fmt.Println()
    fmt.Println("建堆之后：")
    createHeap(unsorted, length)
    for i := 0; i < length; i++ {
        fmt.Printf("%d,", unsorted[i])
    }
    fmt.Printf("\n堆排序之后: \n")
    heapSort(unsorted, length)
    for i := 0; i < length; i++ {
        fmt.Printf("%d,", unsorted[i])
    }
}

运行结果：

[Running] go run "e:\Coding Workspaces\LearningGoTheEasiestWay\Go 数据结构\堆排序\main.go"
建堆之前：
1,7,9,2,4,6,3,5,8,
建堆之后：
9,8,6,7,4,1,3,5,2,
堆排序之后: 
1,2,3,4,5,6,7,8,9,

可以看到，创建堆的结果 ​​9,8,6,7,4,1,3,5,2​​​ 和排序结果 ​​1,2,3,4,5,6,7,8,9​​ 都是和我们图中的堆一样，所以说图看懂了代码也就有意思了。

总结

时间复杂度：堆排序主要耗费时间在初始堆和反复调整堆上，所以时间复杂度为 O(nlogn)

空间复杂度：交换记录需要一个辅助空间，所以空间复杂度为 O(1)

稳定性：堆排序多次交换关键字，可能会发生相等关键字排序前后位置不一样的情况，所以不稳定