【计算理论】计算复杂性 ( NP 类不同表述 | 团问题 | P 对 NP 问题 )
一、NP 类不同表述
N P \rm NP NP 对应的 确定性图灵机 表述 :
N P \rm NP NP 类就是有 多项式时间验证机 的 语言 ( 计算问题 ) 的总体集合 ;
其中的 多项式时间验证机 是一个 确定性图灵机 , 验证机 ;
N P \rm NP NP 对应的 非确定性图灵机 表述 :
N P \rm NP NP 概念转化到 非确定性图灵机 中 , 有另外一个等价定义 ;
如果一个语言属于 N P \rm NP NP , 指的是有一些 非确定性图灵机 可以在 多项式时间 内解决该问题 ;
上述两个定义时等价的 ;
确定性图灵机 多项式时间 内 验证 ,
等价于 ,
非确定性图灵机 多项式时间 内 解决 ;
二、团问题
现在讨论哪些计算问题在 N P \rm NP NP 中 ;
团问题 是一个经典的 N P \rm NP NP 问题 ;
团 是一个无向图 点集 的 子集 , 使得 该点集子集 中 任何两个节点之间都有边相连 ;
团问题 就是 判定无向图中 , 是否包含有 k \rm k k 个节点的 团 ;
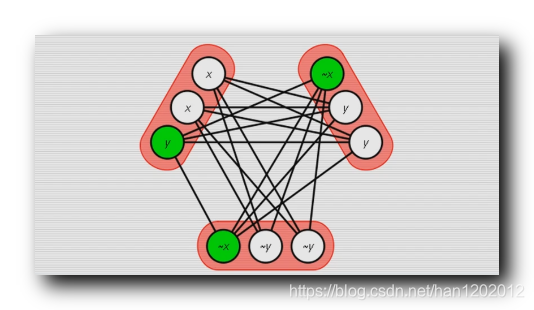
上述团问题 , 是 N P \rm NP NP 问题 ;
给定一个无向图 , 其中有一个 n \rm n n 个节点组成的集合 , 验证该 n \rm n n 集合是否是团 ;
验证的方法就是看这 n \rm n n 元集中的节点之间两两之间是否有边相连即可 ;
验证所花的时间是多项式时间 , 该计算问题在 N P \rm NP NP 中 ;
三、P 对 NP 问题 ( P vs NP )
P \rm P P 对 N P \rm NP NP 问题 是计算机科学中最著名的问题 ;
该问题直接涉及到对计算实质的理解 , 与密码学密切相关 ;
目前没有实质性进展 ;
参考 : 百度百科 - P 对 NP 问题
P ⊆ N P ⊆ E X P T I M E = ⋃ k T I M E ( 2 n k ) \rm P \subseteq NP \subseteq EXPTIME = \bigcup_k TIME(2^{n^k}) P⊆NP⊆EXPTIME=⋃kTIME(2nk)
P \rm P P 是 N P \rm NP NP 的子集 ,
N P \rm NP NP 是 指数级 ( e x p o n e n t \rm exponent exponent ) 时间 ( t i m e \rm time time ) 的子集 ,
非确定性图灵机 , 如果要使用 确定性图灵机 来模仿的话 , 时间复杂度时指数级的 ;
参考博客 【计算理论】计算复杂性 ( 证明 非确定性图灵机 与 确定性图灵机 的时间复杂度 之间的指数关系 )
上述 3 3 3 个不同的复杂类 , 对应的计算模型是不一致的 ,
P \rm P P 对应的是 确定性单个带子图灵机 ,
N P \rm NP NP 对应的是 非确定性的单个带子图灵机 ,
E X P T I M E \rm EXPTIME EXPTIME 对应的是 非确定性的单个带子图灵机 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/111147151
- 点赞
- 收藏
- 关注作者


评论(0)