【计算理论】计算理论总结 ( 非确定性有限自动机 NFA 转为确定性有限自动机 DFA | 示例 ) ★★
一、NFA 转 DFA 示例 1
将下图的 非确定性有限自动机 NFA 转为确定性有限自动机 DFA ;
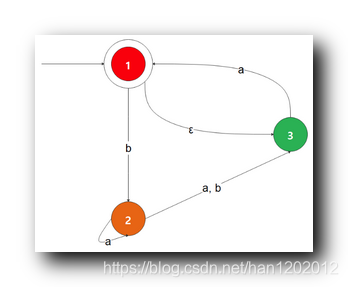
NFA 的状态集 { 1 , 2 , 3 } \rm \{ 1,2,3 \} {1,2,3} , 字符集 { a , b } \rm \{ a,b \} {a,b} ;
从 起始状态 1 1 1 开始分析 , 读取 ε \rm \varepsilon ε 无条件跳转到 3 3 3 , 这里形成了新的状态 { 1 , 3 } \rm \{1, 3\} {1,3} , 写到下面表格中 ;
{ 1 , 3 } \rm \{1, 3\} {1,3} 状态 下读取 a \rm a a 字符结果是 { 1 , 3 } \rm \{1, 3\} {1,3} , 读取 b \rm b b 字符结果是 { 2 } \{2\} {2} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ; 将新状态写到表格中 , 然后分析新状态 ;
{ 2 } \{2\} {2} 状态下读取读取 a \rm a a 字符结果是 { 2 , 3 } \{2,3\} {2,3} , 读取 b \rm b b 字符结果是 { 3 } \{3\} {3} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ; 将新状态写到表格中 , 然后分析新状态 ;
{ 2 , 3 } \{2,3\} {2,3} 状态下读取读取 a \rm a a 字符结果是 { 1 , 2 , 3 } \{1, 2,3\} {1,2,3} , 读取 b \rm b b 字符结果是 { 3 } \{3\} {3} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ; 将新状态写到表格中 , 然后分析新状态 ;
{ 3 } \{3\} {3} 状态下读取读取 a \rm a a 字符结果是 { 1 , 3 } \{1,3\} {1,3} , 读取 b \rm b b 字符结果是 { ∅ } \{ \varnothing \} {∅} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ; 将新状态写到表格中 , 然后分析新状态 ;
{ 1 , 2 , 3 } \{1, 2,3\} {1,2,3} 状态下读取读取 a \rm a a 字符结果是 { 1 , 2 , 3 } \{1, 2,3\} {1,2,3} , 读取 b \rm b b 字符结果是 { 2 , 3 } \{2, 3\} {2,3} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ; 将新状态写到表格中 , 然后分析新状态 ;
{ ∅ } \{ \varnothing \} {∅} 状态下读取读取 a \rm a a 字符结果是 { ∅ } \{ \varnothing \} {∅} , 读取 b \rm b b 字符结果是 { ∅ } \{ \varnothing \} {∅} , 上述分别是 NFA 下两个状态读取字符的后继状态取并集 ;
| a a a | b b b | |
|---|---|---|
| { 1 , 3 } \{1, 3 \} {1,3} | { 1 , 3 } \{1 , 3\} {1,3} | { 2 } \{2\} {2} |
| { 2 } \{2\} {2} | { 2 , 3 } \{2,3\} {2,3} | { 3 } \{3\} {3} |
| { 2 , 3 } \{2,3\} {2,3} | { 1 , 2 , 3 } \{1,2,3\} {1,2,3} | { 3 } \{3\} {3} |
| { 3 } \{3\} {3} | { 1 , 3 } \{1,3\} {1,3} | { ∅ } \{\varnothing \} {∅} |
| { 1 , 2 , 3 } \{1,2,3\} {1,2,3} | { 1 , 2 , 3 } \{1,2,3\} {1,2,3} | { 2 , 3 } \{2,3\} {2,3} |
| { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} |
凡是 包含 NFA 中接受状态 1 1 1 的新状态 都是 接受状态 ;
{ 1 , 3 } \{1, 3 \} {1,3} 和 { 1 , 2 , 3 } \{1, 2, 3 \} {1,2,3} 都是接受状态 , 画图时都是 双圈 ;
空集 { ∅ } \{\varnothing \} {∅} 状态 , 接受任何字符都是空集 { ∅ } \{\varnothing \} {∅} ;
最终的 DFA 如下 :
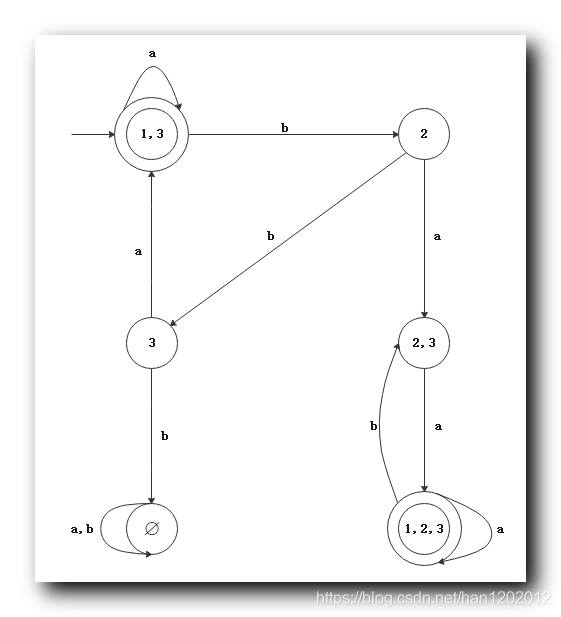
详细推理过程 : 【计算理论】非确定性有限自动机 ( NFA ) 转换成 确定性有限自动机 ( DFA )
二、NFA 转 DFA 示例 2
将下图的 非确定性有限自动机 NFA 转为确定性有限自动机 DFA ;
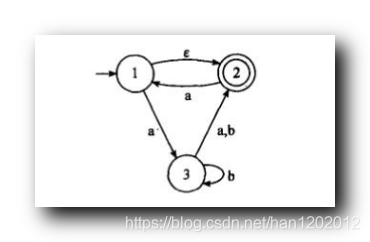
NFA 的状态集 { 1 , 2 , 3 } \rm \{ 1,2,3 \} {1,2,3} , 字符集 { a , b } \rm \{ a,b \} {a,b} ;
从 起始状态 1 1 1 开始分析 , 读取 ε \rm \varepsilon ε 无条件跳转到 2 2 2 , 这里形成了新的状态 { 1 , 2 } \rm \{1, 2\} {1,2} , 写到下面表格中 ;
{ 1 , 2 } \rm \{1, 2\} {1,2} 状态 下读取 a \rm a a 字符结果是 { 1 , 2 , 3 } \rm \{1, 2,3\} {1,2,3} , 读取 b \rm b b 字符结果是 { ∅ } \{\varnothing \} {∅} ;
{ 1 , 2 , 3 } \rm \{1, 2, 3\} {1,2,3} 状态 下读取 a \rm a a 字符结果是 { 1 , 2 , 3 } \rm \{1, 2,3\} {1,2,3} , 读取 b \rm b b 字符结果是 { 2 , 3 } \{2, 3\} {2,3};
{ 2 , 3 } \rm \{ 2, 3\} {2,3} 状态 下读取 a \rm a a 字符结果是 { 1 , 2 } \rm \{1, 2\} {1,2} , 读取 b \rm b b 字符结果是 { 2 , 3 } \{2, 3\} {2,3};
| a a a | b b b | |
|---|---|---|
| { 1 , 2 } \{1, 2 \} {1,2} | { 1 , 2 , 3 } \{1 , 2, 3\} {1,2,3} | { ∅ } \{ \varnothing \} {∅} |
| { 1 , 2 , 3 } \{1 , 2, 3\} {1,2,3} | { 2 , 3 } \{2,3\} {2,3} | { 2 , 3 } \{2,3\} {2,3} |
| { 2 , 3 } \{2,3\} {2,3} | { 1 , 2 } \{1,2\} {1,2} | { 2 , 3 } \{2,3\} {2,3} |
| { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} |
凡是 包含 NFA 中接受状态 2 2 2 的新状态 都是 接受状态 ;
{ 1 , 2 } \{1, 2 \} {1,2} , { 2 , 3 } \{2, 3 \} {2,3} 和 { 1 , 2 , 3 } \{1, 2, 3 \} {1,2,3} 都是接受状态 , 画图时都是 双圈 ;
空集 { ∅ } \{\varnothing \} {∅} 状态 , 接受任何字符都是空集 { ∅ } \{\varnothing \} {∅} ;
最终的 DFA 如下 :
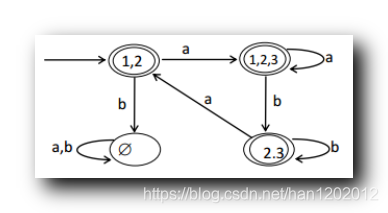
三、NFA 转 DFA 示例 3
将下图的 非确定性有限自动机 NFA 转为确定性有限自动机 DFA ;

NFA 的状态集 { 1 , 2 } \rm \{ 1,2 \} {1,2} , 字符集 { a , b } \rm \{ a,b \} {a,b} ;
从 起始状态 1 1 1 开始分析 ,
{ 1 } \rm \{1\} {1} 状态 下读取 a \rm a a 字符结果是 { 1 , 2 } \rm \{1, 2\} {1,2} , 读取 b \rm b b 字符结果是 { 2 } \{ 2 \} {2} ;
{ 1 , 2 } \rm \{1, 2\} {1,2} 状态 下读取 a \rm a a 字符结果是 { 1 , 2 } \rm \{1, 2\} {1,2} , 读取 b \rm b b 字符结果是 { 1 , 2 } \{1, 2 \} {1,2} ;
{ 2 } \rm \{2\} {2} 状态 下读取 a \rm a a 字符结果是 { ∅ } \{ \varnothing \} {∅} , 读取 b \rm b b 字符结果是 { 1 } \{1\} {1};
| a a a | b b b | |
|---|---|---|
| { 1 } \{1 \} {1} | { 1 , 2 } \{1 , 2\} {1,2} | { 2 } \{ 2 \} {2} |
| { 1 , 2 } \{1 , 2\} {1,2} | { 1 , 2 } \{1, 2\} {1,2} | { 1 , 2 } \{1,2\} {1,2} |
| { 2 } \{2\} {2} | { ∅ } \{ \varnothing \} {∅} | { 1 } \{1\} {1} |
| { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} | { ∅ } \{\varnothing \} {∅} |
凡是 包含 NFA 中接受状态 1 1 1 的新状态 都是 接受状态 ;
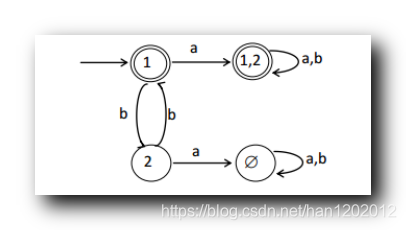
{ 1 } \{1\} {1} 和 { 1 , 2 } \{1, 2 \} {1,2} 都是接受状态 , 画图时都是 双圈 ;
空集 { ∅ } \{\varnothing \} {∅} 状态 , 接受任何字符都是空集 { ∅ } \{\varnothing \} {∅} ;
最终的 DFA 如下 :
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/111386192
- 点赞
- 收藏
- 关注作者


评论(0)