【计算理论】计算理论总结 ( 正则表达式转为非确定性有限自动机 NFA ) ★★
一、正则表达式
1 . 正则表达式原子定义 :
如果 R R R 是
- 字符集 Σ \Sigma Σ 中的 1 1 1 个字符 ,
- 空字符串 ε \varepsilon ε , 或
- 空集 { ∅ } \{ \varnothing \} {∅} ,
那么称 R R R 是正则表达式 ;
2 . 正则表达式递归定义 :
如果 R 1 , R 2 R_1 , R_2 R1,R2 是正则表达式 , 那么
- R 1 ∪ R 2 R_1 \cup R_2 R1∪R2 是正则表达式 ;
- R 1 ∘ R 2 R_1 \circ R_2 R1∘R2 是正则表达式 ;
- R 1 ∗ R_1^* R1∗ 是正则表达式 ;
上述是正则表达式的定义 , 这是一个结构归纳定义 ;
参考博客 :
- 【计算理论】正则语言 ( 正则语言运算 | 正则语言封闭性 )
- 【计算理论】正则语言 ( 正则表达式原子定义 | 正则表达式递归定义 | 正则表达式语言原子定义 | 正则表达式语言结构归纳 | 正则表达式语言示例 | 根据正则表达式构造自动机 )
- 【计算理论】正则语言 ( 推广型的非确定性有限自动机 GNFA | 删除状态 | 确定性有限自动机 转为 正则表达式 )
二、正则语言运算示例 ★
语言计算示例 :
① A A A 语言 : A = { 001 , 10 , , 111 } A = \{ 001 , 10, , 111 \} A={001,10,,111}
② B B B 语言 : B = { ε , 001 } B = \{ \varepsilon , 001 \} B={ε,001}
1 . 并计算 : 将 A , B A,B A,B 两个语言的集合 , 取 并集 即可 , 计算如下 :
A ∪ B = { 001 , 10 , 111 , ε } \rm A \cup B = \{ 001, 10 , 111 , \varepsilon \} A∪B={001,10,111,ε}
2 . 串联计算 : A A A 语言中的任意字符串 , 与 B B B 语言中的任意字符串 , 串联在一起 , A A A 语言中有 3 3 3 个字符串 , B B B 语言中有两个字符串 , 那么串联的结果有 2 × 3 = 6 2 \times 3 = 6 2×3=6 个 , 计算过程如下 :
A ∘ B = { 001 , 10 , 111 , 001001 , 10001 , 111001 } \rm A \circ B = \{ 001 , 10, 111 , 001001, 10001, 111001 \} A∘B={001,10,111,001001,10001,111001}
3 . 星计算 : A A A 语言的星计算 , 该集合一定是一个无限的集合 , 如果 A A A 语言不是空集 , 那么该 A ∗ A^* A∗ 集合个数是无限的 , 其可以由 K K K 个字符串组成 , K K K 取值 0 0 0 到无穷大 , [ 0 , + ∞ ) [0 , +\infty ) [0,+∞) ;
A ∗ = { ε , 001 , 10 , 111 , ⋯ } \rm A^* = \{ \varepsilon , 001 , 10 , 111 , \cdots \} A∗={ε,001,10,111,⋯}
参考博客 :
- 【计算理论】正则语言 ( 正则语言运算 | 正则语言封闭性 )
- 【计算理论】正则语言 ( 正则表达式原子定义 | 正则表达式递归定义 | 正则表达式语言原子定义 | 正则表达式语言结构归纳 | 正则表达式语言示例 | 根据正则表达式构造自动机 )
- 【计算理论】正则语言 ( 推广型的非确定性有限自动机 GNFA | 删除状态 | 确定性有限自动机 转为 正则表达式 )
三、根据正则表达式构造自动机
根据下面的 正则表达式 构造 非确定性有限自动机 ( NFA ) , 刚好能 识别上述正则表达式表示的语言 ;
( a b ∪ a ) ∗ ( ab \cup a )^* (ab∪a)∗
构造能识别 ( a b ∪ a ) ∗ ( ab \cup a )^* (ab∪a)∗ 语言 的 自动机 ;
I. 构造原子自动机 : 先构造能接收 单个字符 的自动机 ;
① 接收 a a a 字符的自动机 : 下面的自动机是可以识别 a a a 字符串的 ;
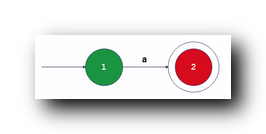
② 接收 b b b 字符的自动机 : 下面的自动机是识别 b b b 字符串的 ;
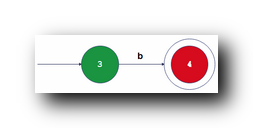
II. 拼装上述识别单个字符的 自动机 :
1 . 摆放自动机位置 : 将 2 2 2 个能识别 a a a 字符串的自动机 , 与 1 1 1 个能识别 b b b 字符串的自动机 , 按照如下排列放置 ;
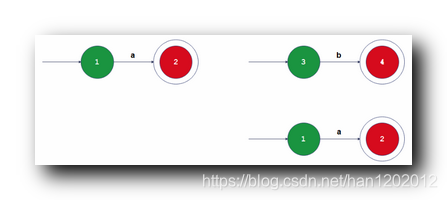
2 . a b ab ab 对应自动机构造 :
① 自动机连接方式 : a a a 正则表达式语言 自动机 与 b b b 正则表达式语言 自动机 是串联在一起的 ;
② 串联两个自动机的状态 : 使用 ε \varepsilon ε 箭头 , 串联 a a a 对应自动机的接受状态 -> b b b 对应自动机的开始状态 ;
③ 修改 前者 的状态 : 同时将 a a a 对应自动机的接受状态 改为非接受状态 ;
下面是 a b ab ab 正则表达式 表达的语言 对应的自动机表示 :
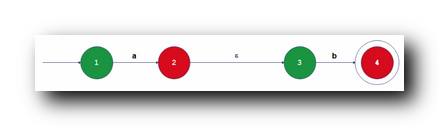
3 . a b ∪ a ab \cup a ab∪a 对应自动机构造 :
① 添加新开始状态 : 重新添加一个开始状态 ;
② 连接并运算前者 : 使用 ε \varepsilon ε 箭头 从这个新添加的开始状态 指向 a b ab ab 自动机开始状态 ;
③ 连接并运算后者 : 使用 ε \varepsilon ε 箭头 从这个新添加的开始状态 指向 a a a 自动机开始状态 ;
下面是 a b ∪ a ab \cup a ab∪a 正则表达式 表达的语言 对应的自动机表示 :
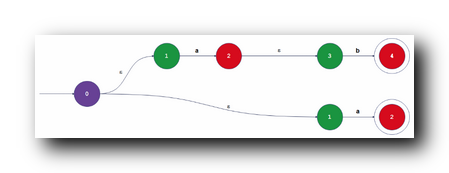
4 . ( a b ∪ a ) ∗ ( ab \cup a )^* (ab∪a)∗ 对应自动机构造 :
① 构造方法 : 就是 在 ( a b ∪ a ) ( ab \cup a ) (ab∪a) 对应自动机的基础上 , 使用 ε \varepsilon ε 箭头 , 从 接受状态 指向 开始状态 ;
② 连接个数 : 所有的接受状态 , 都 使用 ε \varepsilon ε 箭头 指向开始状态 , 这里有两个接受状态 , 需要都指向开始状态 ;
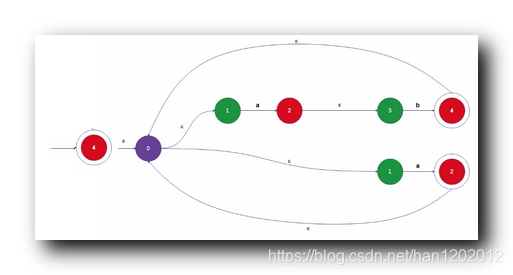
③ 添加新的开始状态 : 添加接受状态作为开始状态 , 指向开始状态 ;
参考博客 :
- 【计算理论】正则语言 ( 正则语言运算 | 正则语言封闭性 )
- 【计算理论】正则语言 ( 正则表达式原子定义 | 正则表达式递归定义 | 正则表达式语言原子定义 | 正则表达式语言结构归纳 | 正则表达式语言示例 | 根据正则表达式构造自动机 )
- 【计算理论】正则语言 ( 推广型的非确定性有限自动机 GNFA | 删除状态 | 确定性有限自动机 转为 正则表达式 )
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/111393044
- 点赞
- 收藏
- 关注作者


评论(0)