【运筹学】表上作业法 ( 找初始基可行解 | 计算检验数 | 调整运量 )

一、运输规划问题
运输规划问题 :
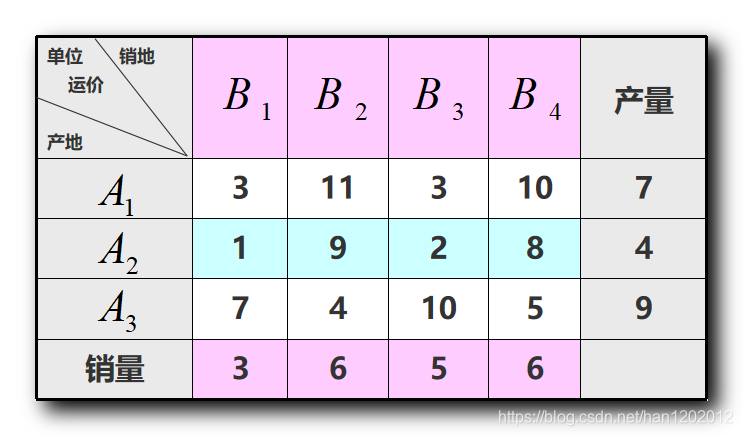
二、找初始基可行解
使用最小元素法求得的初始基可行解 :
| B 1 \rm B_1 B1 | B 2 \rm B_2 B2 | B 3 \rm B_3 B3 | B 4 \rm B_4 B4 | 产量 | |
|---|---|---|---|---|---|
| A 1 \rm A_1 A1 | 3 3 3 | 11 11 11 | 3 3 3 , 4 4 4 | 10 10 10 , 3 3 3 | 7 7 7 |
| A 2 \rm A_2 A2 | 1 1 1 , 3 3 3 | 9 9 9 | 2 2 2 , 1 1 1 | 8 8 8 | 4 4 4 |
| A 3 \rm A_3 A3 | 7 7 7 | 4 4 4 , 6 6 6 | 10 10 10 | 5 5 5 , 3 3 3 | 9 9 9 |
| 销量 | 3 3 3 | 6 6 6 | 5 5 5 | 6 6 6 |
使用 最小元素法, 得到初始基可行解 : { x 13 = 4 x 14 = 3 x 21 = 3 x 23 = 1 x 32 = 6 x 34 = 3
三、计算检验数
计算检验数 :
使用闭回路法 , 逐个计算每个非基变量的检验数 ,
以非基变量为起点 , 出发的格子使用加号 + + + , 第二个格子使用减号 − - − , 之后的歌词依次使用 加号减号交替 + − +- +− 符号 ;
计算上述闭回路的运费代数和 ,
如果代数和 大于等于 0 0 0 , 说明当前的非基变量格子取 0 0 0 就是 最优选择 ;
如果代数和 小于 0 0 0 , 说明当前的非基变量格子取 0 0 0 不是最优选择 ;
这里以计算 σ 24 \rm \sigma_{24} σ24 检验数为例 :
A 24 + \rm A_{24} + A24+ , A 23 − \rm A_{23} - A23− , A 13 + \rm A_{13} + A13+ , A 14 − \rm A_{14} - A14−
σ 24 = ( 1 × 8 ) − ( 1 × 2 ) + ( 1 × 3 ) − ( 1 × 10 ) = − 1 \rm \sigma_{24} = ( 1 \times 8 ) - ( 1 \times 2 ) + ( 1 \times 3 ) - ( 1 \times 10 ) = -1 σ24=(1×8)−(1×2)+(1×3)−(1×10)=−1
检验数小于 0 0 0 ;
计算出的 非基变量 检验数使用 蓝色括号字体 写在表格中 :
| B 1 \rm B_1 B1 | B 2 \rm B_2 B2 | B 3 \rm B_3 B3 | B 4 \rm B_4 B4 | 产量 | |
|---|---|---|---|---|---|
| A 1 \rm A_1 A1 | 3 3 3 , ( 1 ) (1) (1) | 11 11 11 , ( 2 ) (2) (2) | 3 3 3 , 4 4 4 | 10 10 10 , 3 3 3 | 7 7 7 |
| A 2 \rm A_2 A2 | 1 1 1 , 3 3 3 | 9 9 9 , ( 1 ) (1) (1) | 2 2 2 , 1 1 1 | 8 8 8 , ( − 1 ) (-1) (−1) | 4 4 4 |
| A 3 \rm A_3 A3 | 7 7 7 , ( 10 ) (10) (10) | 4 4 4 , 6 6 6 | 10 10 10 , ( 12 ) (12) (12) | 5 5 5 , 3 3 3 | 9 9 9 |
| 销量 | 3 3 3 | 6 6 6 | 5 5 5 | 6 6 6 |
四、调整运量 ( 换基 )
上述检验数中 , σ 24 \rm \sigma_{24} σ24 为负数 , 需要进行换基 , 该非基变量就是入基变量 ;
该检验数的闭合回路如下 : A 24 + \rm A_{24} + A24+ , A 23 − \rm A_{23} - A23− , A 13 + \rm A_{13} + A13+ , A 14 − \rm A_{14} - A14− ;
在 − - − 符号的基变量中挑选一个最小的 , 作为出基变量 ;
换基之后的结果如下 :
经过上述计算后的运费表格如下 :
| B 1 \rm B_1 B1 | B 2 \rm B_2 B2 | B 3 \rm B_3 B3 | B 4 \rm B_4 B4 | 产量 | |
|---|---|---|---|---|---|
| A 1 \rm A_1 A1 | 3 3 3 | 11 11 11 | 3 3 3 , 5 5 5 | 10 10 10 , 2 2 2 | 7 7 7 |
| A 2 \rm A_2 A2 | 1 1 1 , 3 3 3 | 9 9 9 | 2 2 2 | 8 8 8 , 1 1 1 | 4 4 4 |
| A 3 \rm A_3 A3 | 7 7 7 | 4 4 4 , 6 6 6 | 10 10 10 | 5 5 5 , 3 3 3 | 9 9 9 |
| 销量 | 3 3 3 | 6 6 6 | 5 5 5 | 6 6 6 |
计算当前的总运费 :
( 3 × 5 ) + ( 10 × 2 ) + ( 1 × 3 ) + ( 8 × 1 ) + ( 4 × 6 ) + ( 3 × 5 ) = 85 \rm ( 3 \times 5 ) + ( 10 \times 2 ) + ( 1 \times 3 ) + ( 8 \times 1 ) + ( 4 \times 6 ) + ( 3 \times 5 ) = 85 (3×5)+(10×2)+(1×3)+(8×1)+(4×6)+(3×5)=85
计算检验数验证 , 是最优解 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/112303439
- 点赞
- 收藏
- 关注作者

评论(0)