一、整数规划问题解的特征

整数规划问题解的特征 :

① 整数规划问题 与 松弛问题 可行解集合关系 : 整数规划问题 可行解集合 , 是该整数规划问题的 松弛问题 可行解集合 的子集 , 任意两个可行解的 凸组合 , 不一定满足整数约束条件 , 不一定是可行解 ;

② 整数规划问题 与 松弛问题 最优解关系 : 整数规划问题的可行解 一定是 其 松弛问题的可行解 , 松弛问题的可行解不一定是整数规划问题的可行解 , 整数规划问题的最优解 不会优于 松弛问题的最优解 ;

松弛问题 比 整数规划问题 条件少一些 , 整数规划问题比松弛问题变量限制多一条 " 约束变量必须都是整数 " ;

二、整数规划问题 与 松弛问题 示例

假设有如下整数规划问题 :

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0   并 且 为 整 数

上述整数规划问题对应的松弛问题 : 松弛问题 比 整数规划问题 条件少一些 , 整数规划问题比松弛问题变量限制多一条 " 约束变量必须都是整数 " ;

m a x Z = x 1 + x 2 s . t { 14 x 1 + 9 x 2 ≤ 51 − 6 x 1 + 3 x 2 ≤ 1 x 1 , x 2 ≥ 0

使用图解法 , 解上述 松弛问题 的最优解为 { x 1 = 3 2 x 2 = 10 3

此时目标函数值 $\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{Z}={\mathrm{x}}_1+{\mathrm{x}}_2=\frac{29}{6}$

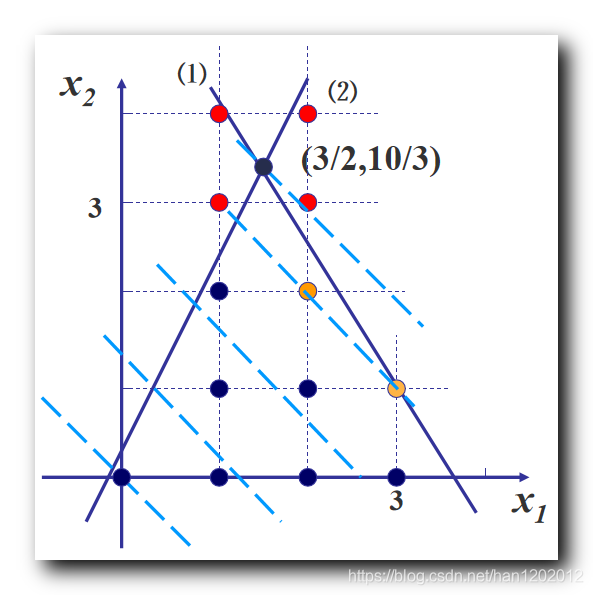
简单的将其松弛问题最优解上下取整 , 得到的四个点 , 如上图的四个红色点 , 都不在可行域中 , 选择的整数解 , 必须在可行域中 ;

根据 整数规划问题的的松弛问题 的最优解 , 如何找其 整数规划问题 的整数最优解 , 是整数规划问题的核心问题 ;

穷举法 ( 有局限性 ) : 直接看上图中可行域内的整数点 , 然后再逐一代入目标函数 , 得到一个 整数规划问题 的最优解 , 但是这种方法无法推广应用 , 如果点的个数比较多 , 如几万个 , 变量的维数多 , 如 $10$ 个约束变量 , 这种方法肯定不适用 ;

整数规划问题的求解方法有 : ① 分支定界法 , ② 割平面法 ;

推荐使用 分支定界法 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/112464321