【运筹学】匈牙利法 ( 匈牙利法步骤 | 试指派调整矩阵原理分析 | 打 √ | 直线覆盖 )
一、指派问题求解步骤
指派问题求解步骤 :
1 . 使行列出现 0 0 0 元素 : 指派问题系数矩阵 ( c i j ) (c_{ij}) (cij) 变换为 ( b i j ) (b_{ij}) (bij) 系数矩阵 , 在 ( b i j ) (b_{ij}) (bij) 矩阵中 每行 每列 都出现 0 0 0 元素 ;
-
每行都出现 0 0 0 元素 : ( c i j ) (c_{ij}) (cij) 系数矩阵中 , 每行都 减去该行最小元素 ;
-
每列都出现 0 0 0 元素 : 在上述变换的基础上 , 每列元素中 减去该列最小元素 ;
注意必须先变行 , 然后再变列 , 行列不能同时进行改变 ; 否则矩阵中会出现负数 , 该矩阵中 不能出现负数 ;
2 . 试指派 : 进行尝试指派 , 寻求最优解 ;
在 ( b i j ) (b_{ij}) (bij) 系数矩阵 中找到尽可能多的 独立 0 0 0 元素 , 如果能找到 n n n 个独立 0 0 0 元素 , 以这 n n n 个独立 0 0 0 元素对应解矩阵 ( x i j ) (x_{ij}) (xij) 中的元素为 1 1 1 , 其余元素为 0 0 0 , 这样就得到最优解 ;
二、打 √
分析 【运筹学】匈牙利法 ( 匈牙利法步骤 | 第二步 : 试指派操作示例 ) 博客中试指派调整矩阵的原理 ;
下面的矩阵是完成第一步操作后 , 得到的行列都有 0 0 0 的元素的系数矩阵 ( b i j ) (b_{ij}) (bij) :
( b i j ) = [ 4 5 4 0 0 1 0 4 2 0 4 3 3 7 1 0 ] (b_{ij}) =
试指派后的结果如下 :
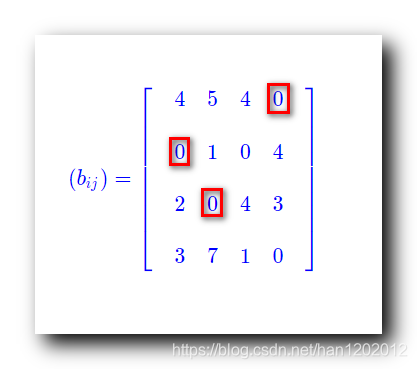
定位一个没有独立 0 0 0 元素的行 : 先对没有 0 0 0 元素的行打钩 √ : 第 4 4 4 行没有独立 0 0 0 元素 , 第 4 4 4 行打 √ ;
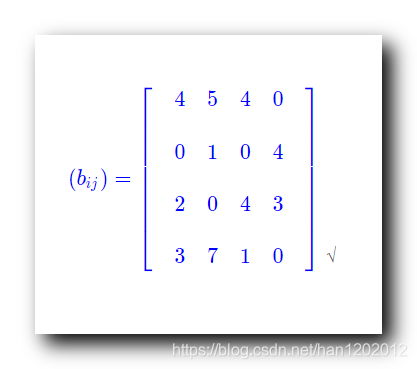
讨论第 4 4 4 行 : 第 4 4 4 行没有独立的 0 0 0 元素 , 但是有废弃的 0 0 0 元素 , 因为在第一步已经保证了每行每列都有 0 0 0 元素 ;
在第 4 4 4 行 0 0 0 元素所在列 , 即第 4 4 4 列 , 打 √ ;
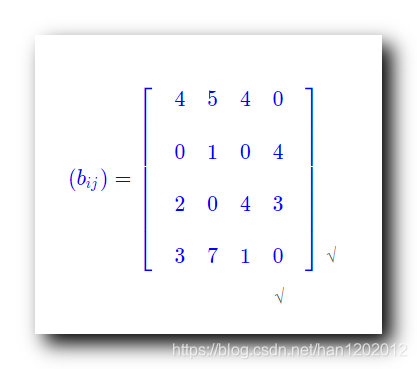
讨论第 4 4 4 列 : 上述打钩的列中 , 查看是否有 独立的 0 0 0 元素 , 如果有对应的行就打 √ ;
第 1 1 1 行有独立的 0 0 0 元素 , 在第 1 1 1 行位置打 √ ;
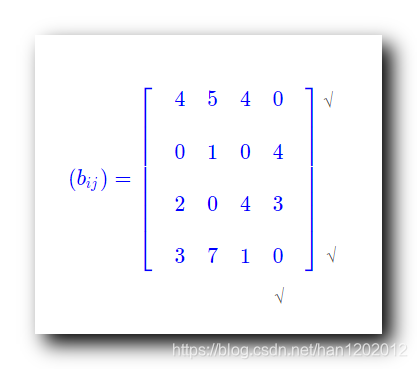
讨论第 1 1 1 行 : 查看第 1 1 1 行是否有废弃的 0 0 0 元素 , 如果有就继续打 √ , 如果没有就停止 ;
第 1 1 1 行没有废弃的 0 0 0 元素 , 直接停止 ;
讨论 行 的时候讨论的是 废弃的 0 0 0 元素 ,
讨论 列 的时候讨论的是 独立的 0 0 0 元素 ;
三、直线覆盖
打 √ 完毕 , 开始讨论覆盖 ,
没有 打 √ 的行划线 , 打 √ 的列划线 , 三条线就将所有的 0 0 0 元素覆盖了 ,
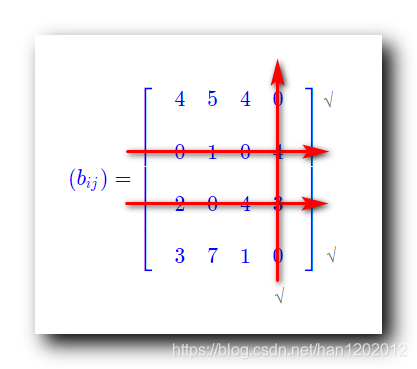
在没有被覆盖的元素中 , 找最小的元素 1 1 1 , 将该元素所在的没有覆盖的行 − 1 -1 −1 , 覆盖的列 + 1 +1 +1 ;
最终得到如下矩阵 :
( b i j ) = [ 3 4 3 0 0 1 0 5 2 0 4 4 2 6 0 0 ] (b_{ij}) =
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/112600842
- 点赞
- 收藏
- 关注作者


评论(0)