【计算理论】上下文无关语法 ( CFG ) 转为 下推自动机 ( PDA )
I . 上下文无关语法 ( CFG ) 转为 下推自动机 ( PDA )
上下文无关语法 ( CFG ) :
S → a T b ∣ b S \to aTb | b S→aTb∣b
T → T a ∣ ε T \to Ta|\varepsilon T→Ta∣ε
将上述 上下文无关语法 ( CFG ) 转为 下推自动机 ;
II . 下推自动机 ( PDA ) 三个状态
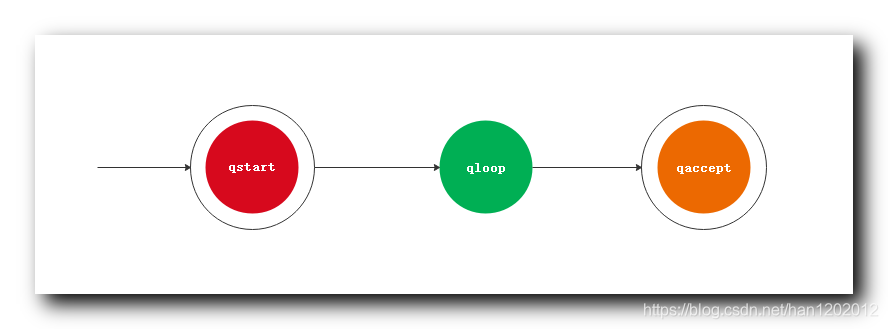
该 自动机 共包含 3 3 3 个状态 , q s t a r t q_{start} qstart , q l o o p q_{loop} qloop , q a c c e p t q_{accept} qaccept , 最后一个状态是 可接受状态 ;
III . 下推自动机 ( PDA ) q s t a r t q_{start} qstart 状态
1 . 首先在 栈顶 放入 K K K 字符 , 用于当做栈底的标识 ;
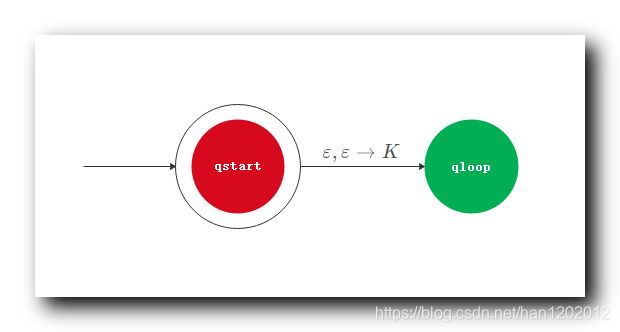
生成指令 : ε , ε → K \varepsilon , \varepsilon \to K ε,ε→K ;
开始状态 q s t a r t q_{start} qstart 状态 , 读取 ε , ε → K \varepsilon , \varepsilon \to K ε,ε→K 指令 , 读取空字符 , 使用 K K K 替换栈顶的空字符 , 就是将 K K K 放入栈中 ;
状态跳转 : 之后跳转到 q l o o p q_{loop} qloop 状态 ;
当前的 下推自动机 ( CFG ) 设计 :
IV . 下推自动机 ( PDA ) q l o o p q_{loop} qloop 状态
1 . q l o o p q_{loop} qloop 状态下 在栈中模仿 上下文无关语法 ( CFG ) 的规则替换 ;
上下文无关语法 ( CFG ) :
S → a T b ∣ b S \to aTb | b S→aTb∣b
T → T a ∣ ε T \to Ta|\varepsilon T→Ta∣ε
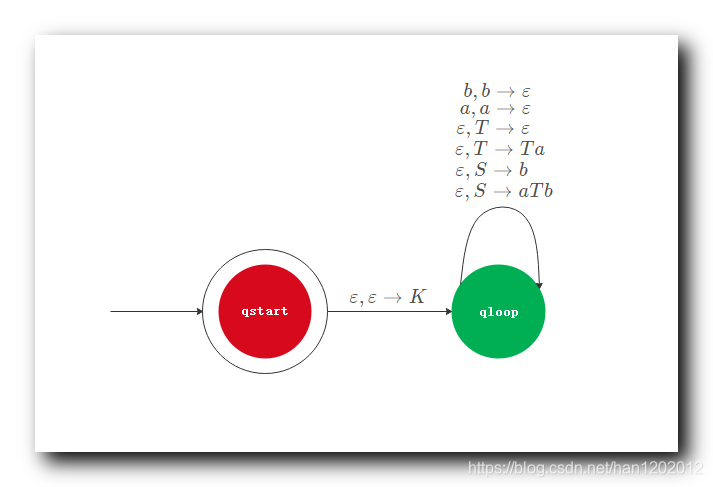
2 . 对照上述 上下文无关语法 ( CFG ) , 逐条生成指令 :
① S → a T b S \to aTb S→aTb 对应的指令 : ε , S → a T b \varepsilon , S \to aTb ε,S→aTb , 读取 ε \varepsilon ε 时 , 使用 a T b aTb aTb 替换栈顶的 S S S ; 即如果栈顶是 S S S , 使用 a T b aTb aTb 替换栈顶的 S S S ;
② S → b S \to b S→b 对应的指令 : ε , S → b \varepsilon , S \to b ε,S→b , 读取 ε \varepsilon ε 时 , 使用 b b b 替换栈顶的 S S S ; 即如果栈顶是 S S S , 使用 b b b 替换栈顶的 S S S ;
③ T → T a T \to Ta T→Ta 对应的指令 : ε , T → T a \varepsilon , T \to Ta ε,T→Ta , 读取 ε \varepsilon ε 时 , 使用 T a Ta Ta 替换栈顶的 T T T ; 即如果栈顶是 T T T , 使用 T a Ta Ta 替换栈顶的 T T T ;
④ T → ε T \to \varepsilon T→ε 对应的指令 : ε , T → ε \varepsilon , T \to \varepsilon ε,T→ε , 读取 ε \varepsilon ε 时 , 使用 ε \varepsilon ε 替换栈顶的 T T T ; 即如果栈顶是 T T T , 使用 ε \varepsilon ε 替换栈顶的 T T T ;
⑤ 如果栈上有终端字符 a a a , 要将栈里的终端字符 a a a 移除 , 对应指令是 a , a → ε a , a \to \varepsilon a,a→ε , 如果读取到字符 a a a 时 , 从栈顶将字符 a a a 移除 ;
⑥ 如果栈上有终端字符 b b b , 要将栈里的终端字符 b b b 移除 , 对应指令是 b , b → ε b , b \to \varepsilon b,b→ε , 如果读取到字符 b b b 时 , 从栈顶将字符 b b b 移除 ;
V . 下推自动机 ( PDA ) q a c c e p t q_{accept} qaccept 状态
1 . q a c c e p t q_{accept} qaccept 状态 :
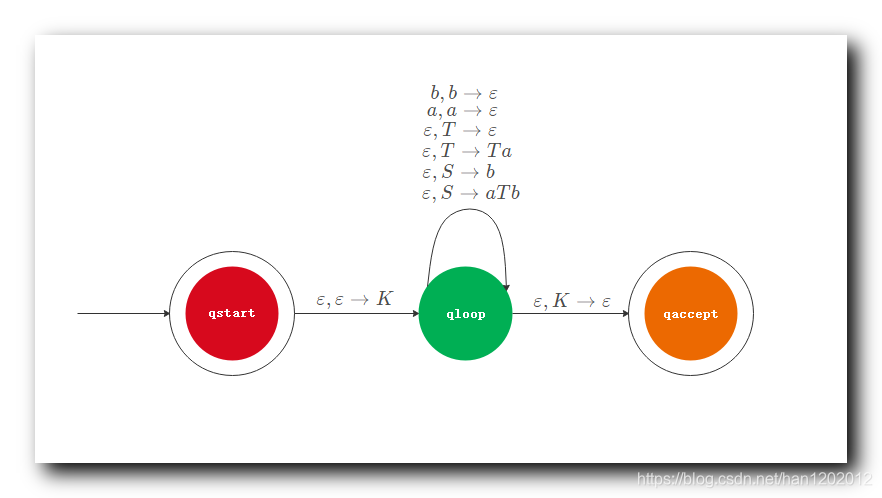
在 q l o o p q_{loop} qloop 状态下 , 将栈内的除 K K K 外所有的字符都移除完毕 , 开始向 q a c c e p t q_{accept} qaccept 状态跳转 ;
此时需要生成指令 ε , K → ε \varepsilon , K \to \varepsilon ε,K→ε , 读取 空字符 ε \varepsilon ε , 使用 空字符 ε \varepsilon ε 替换栈顶的 K K K 字符 , 此时栈清空了 ;
VI . 下推自动机 ( PDA ) 指令分解
1 . 非法指令分解
上述生成的
- ε , S → a T b \varepsilon , S \to aTb ε,S→aTb
- ε , T → T a \varepsilon , T \to Ta ε,T→Ta
两个指令是不合法的 , 在栈中 , 一个字符 ( 或空字符串 ε \varepsilon ε ) 只能由 一个字符 ( 或空字符串 ε \varepsilon ε ) 替换 ;
上述不合法的规则 , 多个字符替换栈顶的一个字符 , 需要进行分解操作 ;
2 . ε , S → a T b \varepsilon , S \to aTb ε,S→aTb 指令分解流程 :
① q l o o p q_{loop} qloop 状态 跳转到 新的状态 q l o o p 1 q_{loop1} qloop1 , 跳转读取的指令时 ε , S → b \varepsilon , S \to b ε,S→b , 读取空字符 , 然后使用 b b b 替换栈顶的 S S S 字符 ;
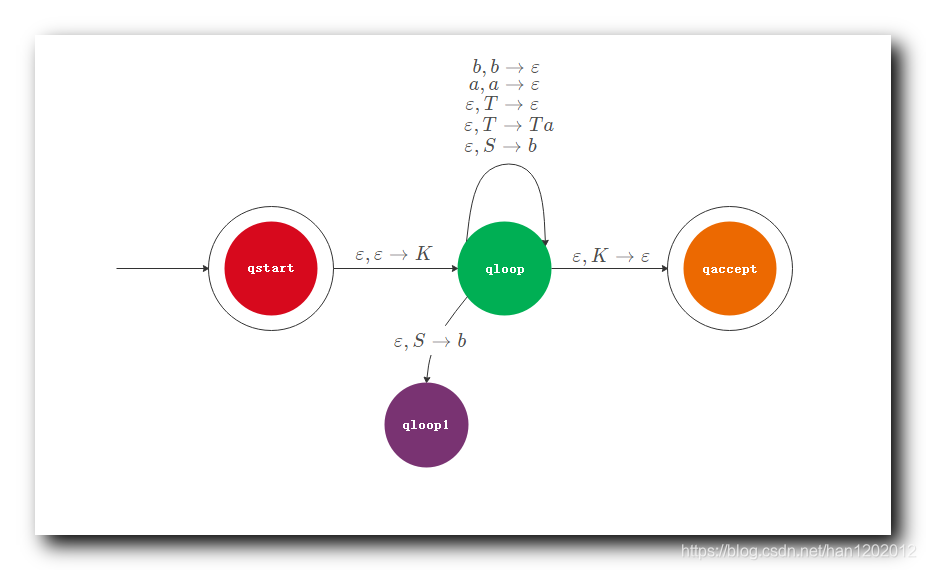
② q l o o p 1 q_{loop1} qloop1 状态 跳转到 新的状态 q l o o p 2 q_{loop2} qloop2 , 跳转读取的指令时 ε , ε → T \varepsilon , \varepsilon \to T ε,ε→T , 读取空字符 , 然后使用 T T T 替换栈顶的 ε \varepsilon ε 字符 , 相当于在栈中放入了 T T T 字符 ;
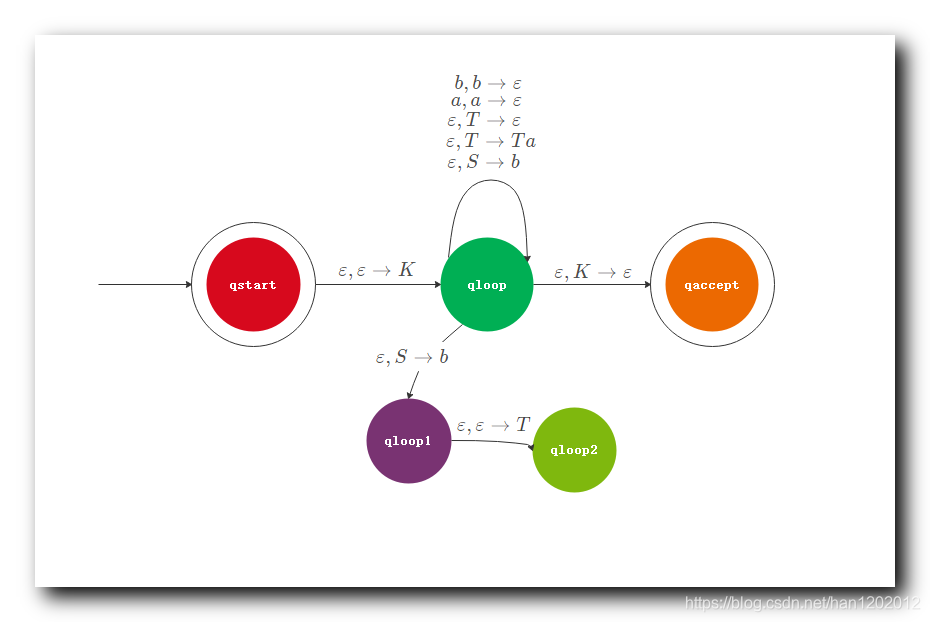
③ q l o o p 2 q_{loop2} qloop2 状态 跳转到 原来的状态 q l o o p q_{loop} qloop , 跳转读取的指令时 ε , ε → a \varepsilon , \varepsilon \to a ε,ε→a , 读取空字符 , 然后使用 a a a 替换栈顶的 ε \varepsilon ε 字符 , 相当于在栈中放入了 a a a 字符 ;
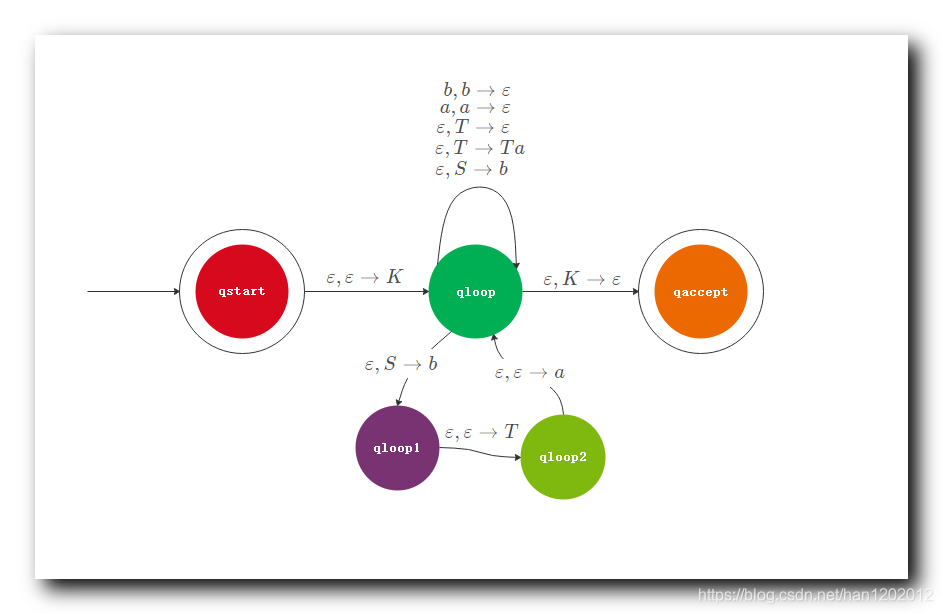
分解 ε , S → a T b \varepsilon , S \to aTb ε,S→aTb 后的 3 3 3 个指令 :
- ε , S → b \varepsilon , S \to b ε,S→b
- ε , ε → T \varepsilon , \varepsilon \to T ε,ε→T
- ε , ε → a \varepsilon , \varepsilon \to a ε,ε→a
上述三个指令都是合法的 , 上述 3 3 3 个指令 串联后的效果等价于 ε , S → a T b \varepsilon , S \to aTb ε,S→aTb 操作 , 等价于上下文无关语法的 S → a T b S \to aTb S→aTb 规则效果 ;
3 . ε , T → T a \varepsilon , T \to Ta ε,T→Ta 指令分解流程 :
① q l o o p q_{loop} qloop 状态 跳转到 新的状态 q l o o p 3 q_{loop3} qloop3 , 跳转读取的指令时 ε , S → a \varepsilon , S \to a ε,S→a , 读取空字符 , 然后使用 a a a 替换栈顶的 S S S 字符 ;
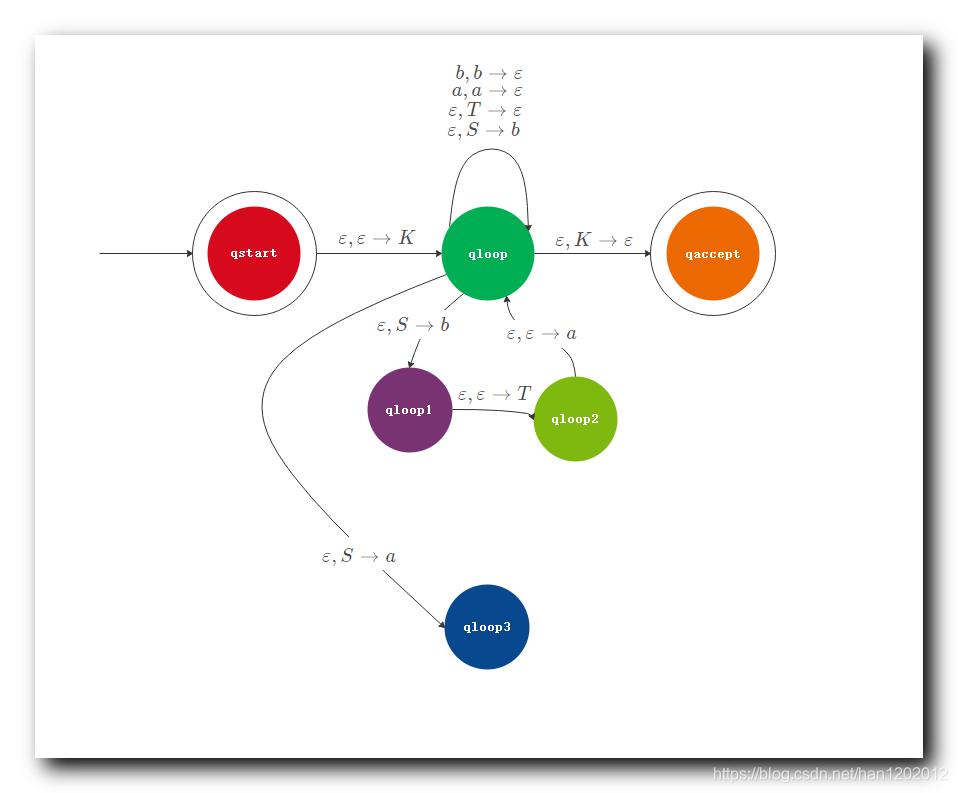
② q l o o p 3 q_{loop3} qloop3 状态 跳转到 原来的状态 q l o o p q_{loop} qloop , 跳转读取的指令时 ε , ε → T \varepsilon , \varepsilon \to T ε,ε→T , 读取空字符 , 然后使用 T T T 替换栈顶的 ε \varepsilon ε 字符 , 相当于在栈中放入了 T T T 字符 ;
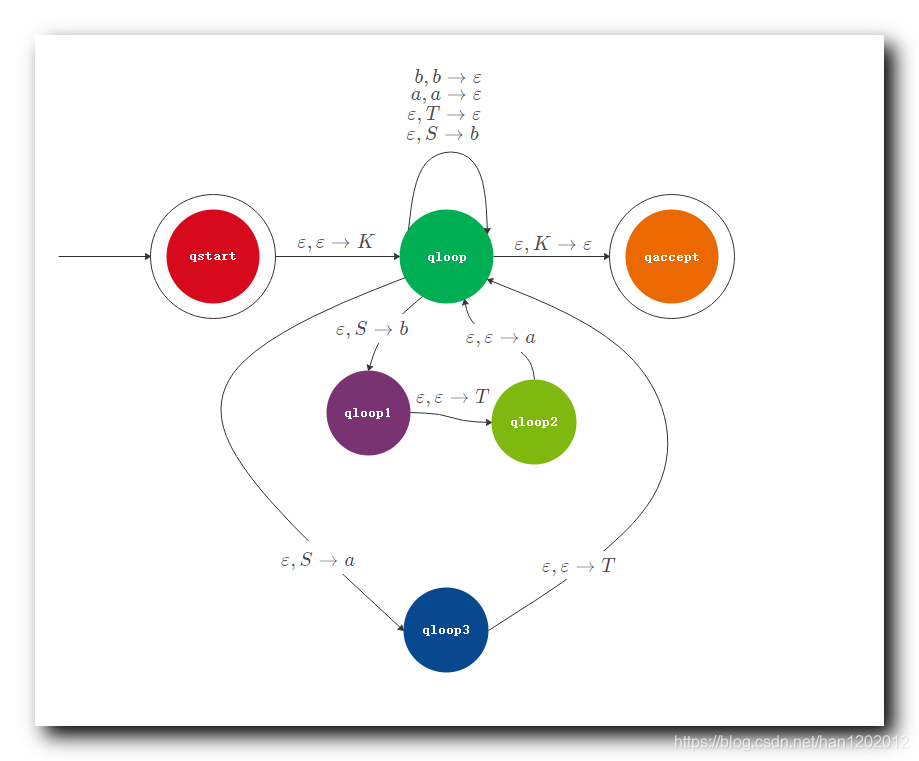
分解 ε , T → T a \varepsilon , T \to Ta ε,T→Ta 后的 2 2 2 个指令 :
- ε , S → a \varepsilon , S \to a ε,S→a
- ε , ε → T \varepsilon , \varepsilon \to T ε,ε→T
上述 2 2 2 个指令都是合法的 , 上述 2 2 2 个指令 串联后的效果等价于 ε , T → T a \varepsilon , T \to Ta ε,T→Ta 指令 , 等价于上下文无关语法的 T → T a T \to Ta T→Ta 规则效果 ;
VII . 最终转换成的 下推自动机 ( PDA ) 结果
最终的 上下文无关语法 ( CFG ) 转为的 下推自动机 ( PDA ) 样式 :
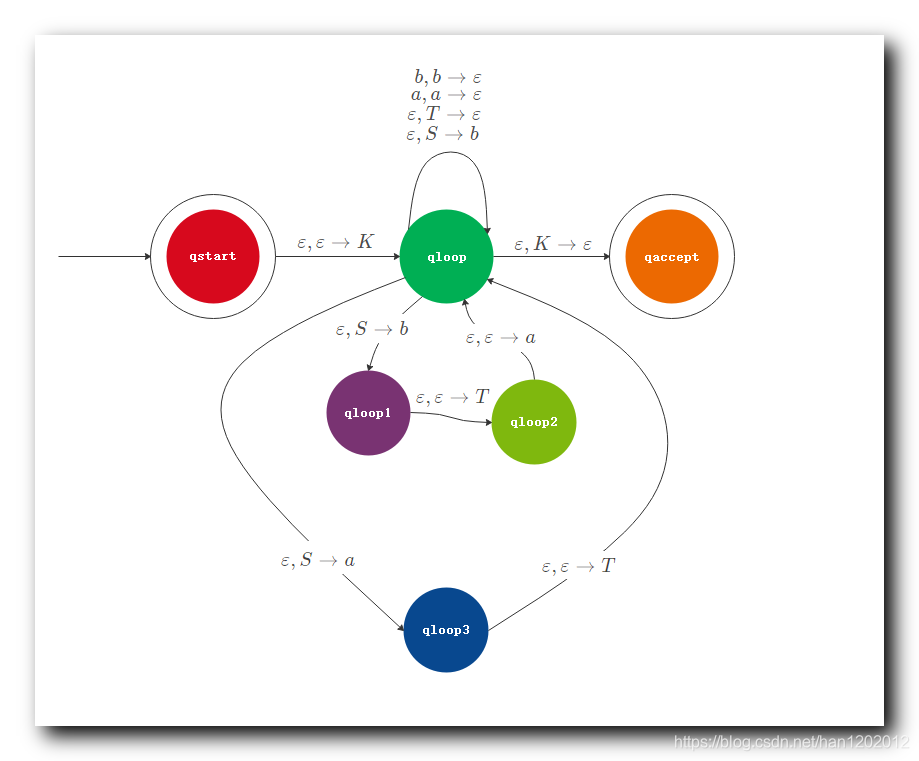
上下文无关语法 ( CFG ) 与 下推自动机 ( PDA ) 是等价的 , 给定一个 下推自动机 ( PDA ) , 构造 上下文无关语法 ( CFG ) , 该语法生成的语言 , 就是该 下推自动机 ( PDA ) 所认识的语言 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/106244977
- 点赞
- 收藏
- 关注作者


评论(0)