【运筹学】对偶理论 : 对偶性质 ( 对称性质 | 对称性质推导 )
一、对称性质
对称性定理 :
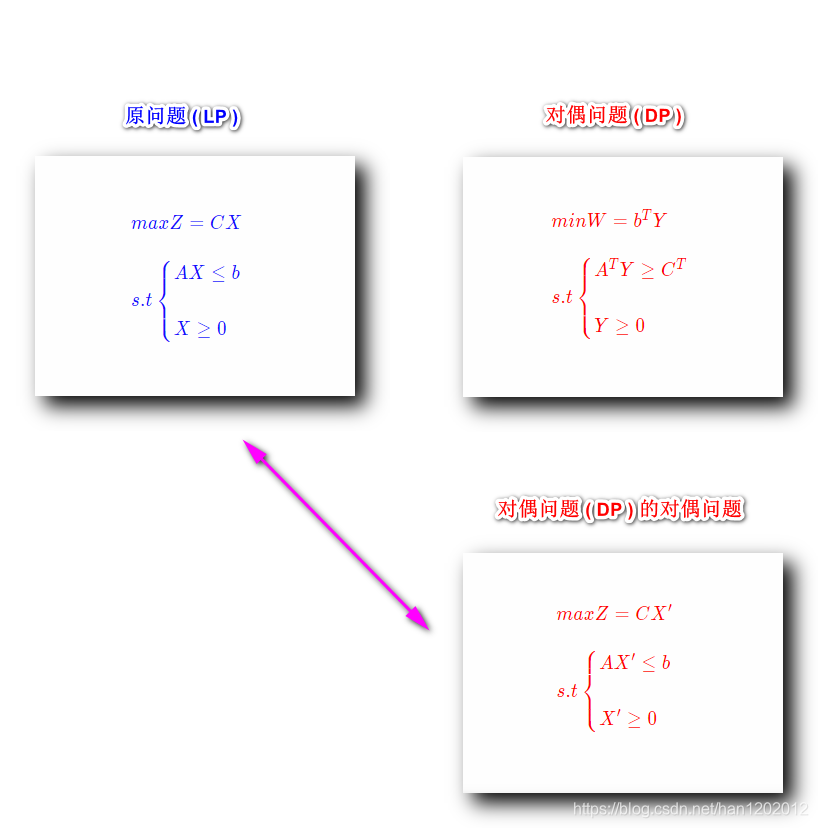
- 原问题 ( L P LP LP ) 的 对偶 是 对偶问题 ( D P DP DP )
- 对偶问题 ( D P DP DP ) 的 对偶 是 原问题 ( L P LP LP )
原问题 和 对偶问题 互为对偶 ;
对偶问题是对称的
原问题 L P LP LP :
m a x Z = C X s . t { A X ≤ b X ≥ 0
对偶问题 D P DP DP :
m i n W = b T Y s . t { A T Y ≥ C T Y ≥ 0
二、对称性质推导
将上述 对偶问题 D P DP DP 转为求最大值 ;
m i n W = b T Y s . t { A T Y ≥ C T Y ≥ 0
转换过程 :
- 目标函数转为取最大值 : 转换后的结果如下 , 就是相当于在目标函数的左右两端乘以 − 1 -1 −1 ;
m a x Z = − b T Y s . t { A T Y ≥ C T Y ≥ 0
- 根据下面表格中的对偶问题写法 , 写出上述线性规划的对偶问题 :
- 目标函数由最大值转为最小值 ( 目标函数求最大值前提 ) : m i n W = C X min W = CX minW=CX
- L P LP LP 约束条件与 D P DP DP 约束变量符号相反 ( 目标函数求最大值前提 ) : 上述线性规划问题的 约束条件是大于等于不等式 , 那么对应的 约束变量小于等于 0 0 0 ; 约束变量 X ≤ 0 X \leq 0 X≤0
- L P LP LP 约束变量 与 D P DP DP 约束条件符号相同 ( 目标函数求最大值前提 ) : 上述线性规划问题的 约束变量大于等于 0 0 0 , 那么对应的 约束条件也是大于等于不等式 ; 约束条件是 A X ≥ − b AX \geq -b AX≥−b
- 最终得到的线性规划为 :
m i n W = C X s . t { A X ≥ − b X ≤ 0
| 原问题 L P LP LP | 对偶问题 D P DP DP |
|---|---|
| – | – |
| 目标函数求最大值 m a x Z maxZ maxZ | 目标函数求最小值 m i n W minW minW |
| – | – |
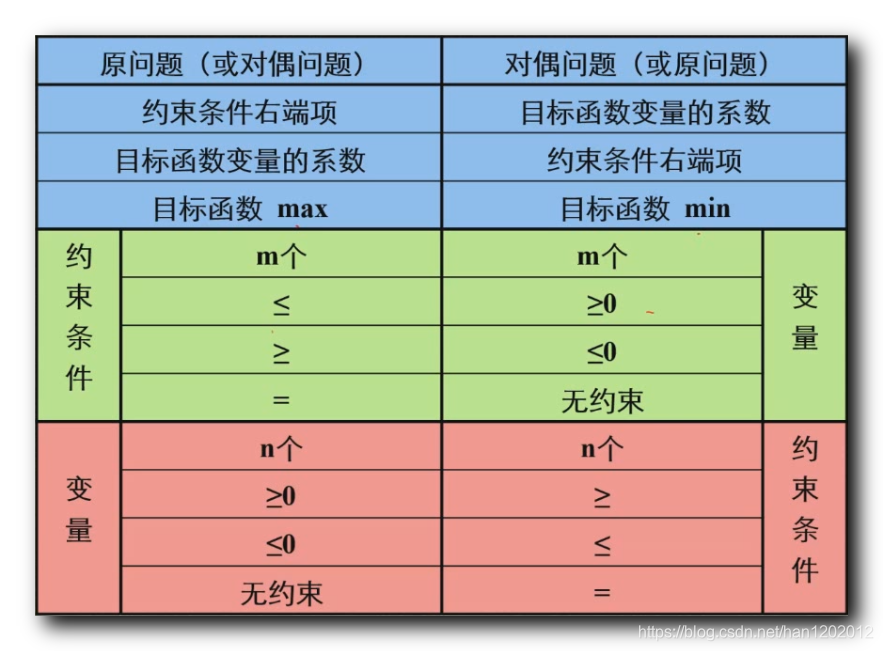
| 约束条件常数项 | 目标函数系数 |
| 目标函数系数 | 约束条件常数项 |
| – | – |
| m m m 个约束条件 | n n n 个约束变量 |
| n n n 个约束变量 | m m m 个约束条件 |
| – | – |
| 约束条件是小于等于不等式 ≤ \leq ≤ | 约束变量是大于等于 ≥ 0 \geq 0 ≥0 的 |
| 约束条件是大于等于不等式 ≥ \geq ≥ | 约束变量是小于等于 ≤ 0 \leq 0 ≤0 的 |
| 约束条件是等式 | 约束变量是自由变量 ( 没有约束 ) |
| – | – |
| 约束变量是大于等于 ≥ 0 \geq 0 ≥0 的 | 约束条件是大于等于不等式 ≥ \geq ≥ |
| 约束变量是小于等于 ≤ 0 \leq 0 ≤0 的 | 约束条件是小于等于不等式 ≤ \leq ≤ |
| 约束变量是自由变量 ( 没有约束 ) | 约束条件是等式 |
记住一条 : 目标函数求最大值 , L P LP LP 约束条件与 D P DP DP 约束变量符号相反 , L P LP LP 约束变量 与 D P DP DP 约束条件符号相同 ;
对如下线性规划作代换 :
m i n W = C X s . t { A X ≥ − b X ≤ 0
代换内容 : 引入变量 X ′ = − X X' = -X X′=−X , 使用 − X ′ -X' −X′ 替换上述线性规划中的 X X X ;
- 目标函数 : 代换后为 m i n W = − C X ′ minW = -CX' minW=−CX′ , 此时两边乘以 − 1 -1 −1 即可得到 m a x Z = C X ′ maxZ = CX' maxZ=CX′ ;
- 约束方程 : 代换后为 − A X ′ ≥ − b -AX' \geq -b −AX′≥−b , 左右两边乘以 − 1 -1 −1 即可得到 A X ′ ≤ b AX' \leq b AX′≤b ;
- 约束变量 : 代换后为 − X ′ ≤ 0 -X' \leq 0 −X′≤0 , 左右变量乘以 − 1 -1 −1 即可得到 X ′ ≥ 0 X' \geq 0 X′≥0
最终代换结果为 :
m a x Z = C X ′ s . t { A X ′ ≤ b X ′ ≥ 0
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/107722928
- 点赞
- 收藏
- 关注作者


评论(0)