【计算理论】非确定性有限自动机 ( 计算过程 | 计算树 | 确定可接受字符串 | 设计非确定性有限自动机 | 空字符 )
一、非确定性自动机 计算过程 ( 计算树 )
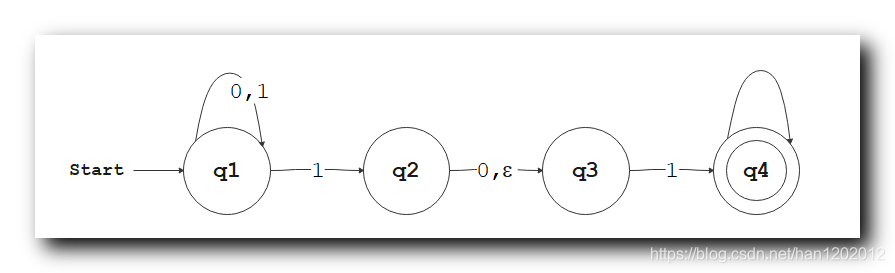
分析上述自动机处理 " 0101 0101 0101 " 字符串信息的过程
自动机启动后 , 进入 q 1 \rm q_1 q1 状态 , 这是个非接受状态 ( 单圈表示 ) ;
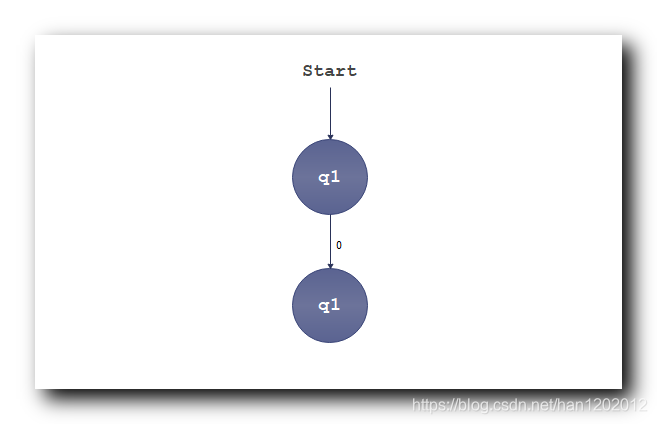
q 1 q_1 q1 状态读取字符 0 0 0 : 仍然保持 q 1 \rm q_1 q1 状态 ;
q 1 \rm q_1 q1 状态 读取字符 1 1 1 : 有 3 3 3 个后继状态 , 分别是 q 1 \rm q_1 q1 , q 2 \rm q_2 q2 和 q 3 \rm q_3 q3 ;
q 3 q_3 q3 是 q 1 q_1 q1 输入 1 1 1 的后继状态原因 : q 2 q_2 q2 到 q 3 q_3 q3 不需要读取任何字符 , 就可以跳转到 q 3 q_3 q3 , 因此 q 2 q_2 q2 是无条件跳转到 q 3 q_3 q3 的 , 此时可以与 q 2 q_2 q2 并列 ;
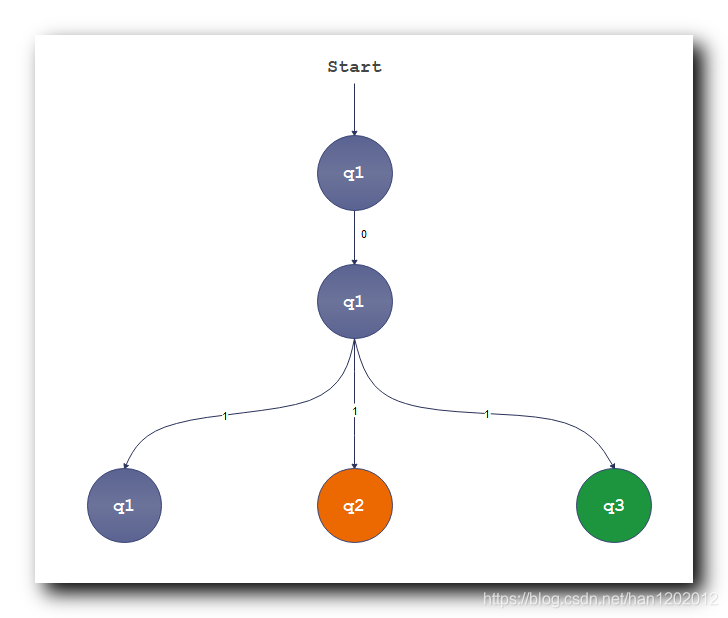
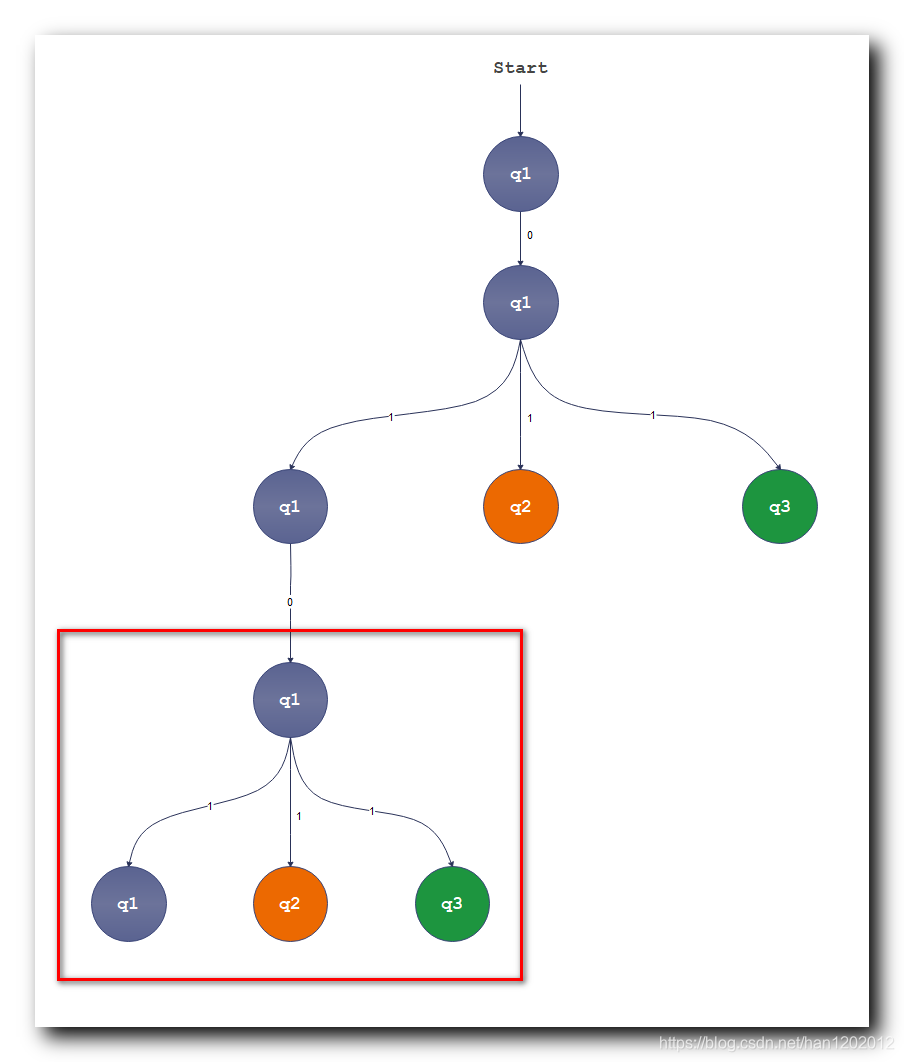
分析第三层的左侧 q 1 q_1 q1 分支 :
q 1 q_1 q1 状态读取 0 0 0 , 跳转到 q 1 q_1 q1 状态 ;
再次从 q 1 q_1 q1 状态读取 1 1 1 , 又出现跳转到 q 1 q_1 q1 , q 2 q_2 q2 和 q 3 q_3 q3 三个状态的分支 , 如下图红框内的部分 :
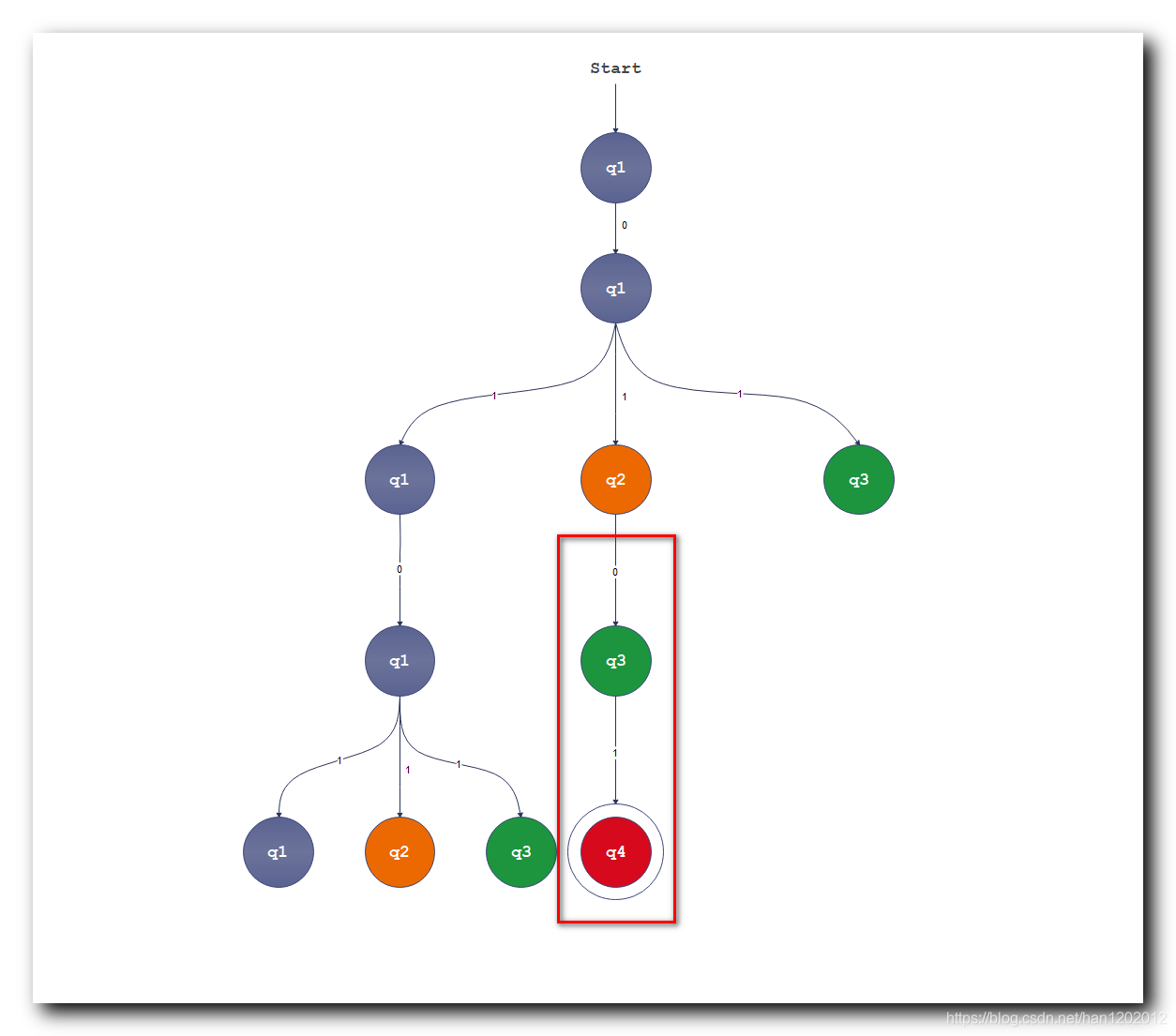
分析第三层的中间 q 2 q_2 q2 分支 :
q 2 q_2 q2 状态读取 0 0 0 , 跳转到 q 3 q_3 q3 状态 ;
再次从 q 3 q_3 q3 状态读取 1 1 1 , 跳转到 q 4 q_4 q4 状态 , 如下图红框内的部分 ;
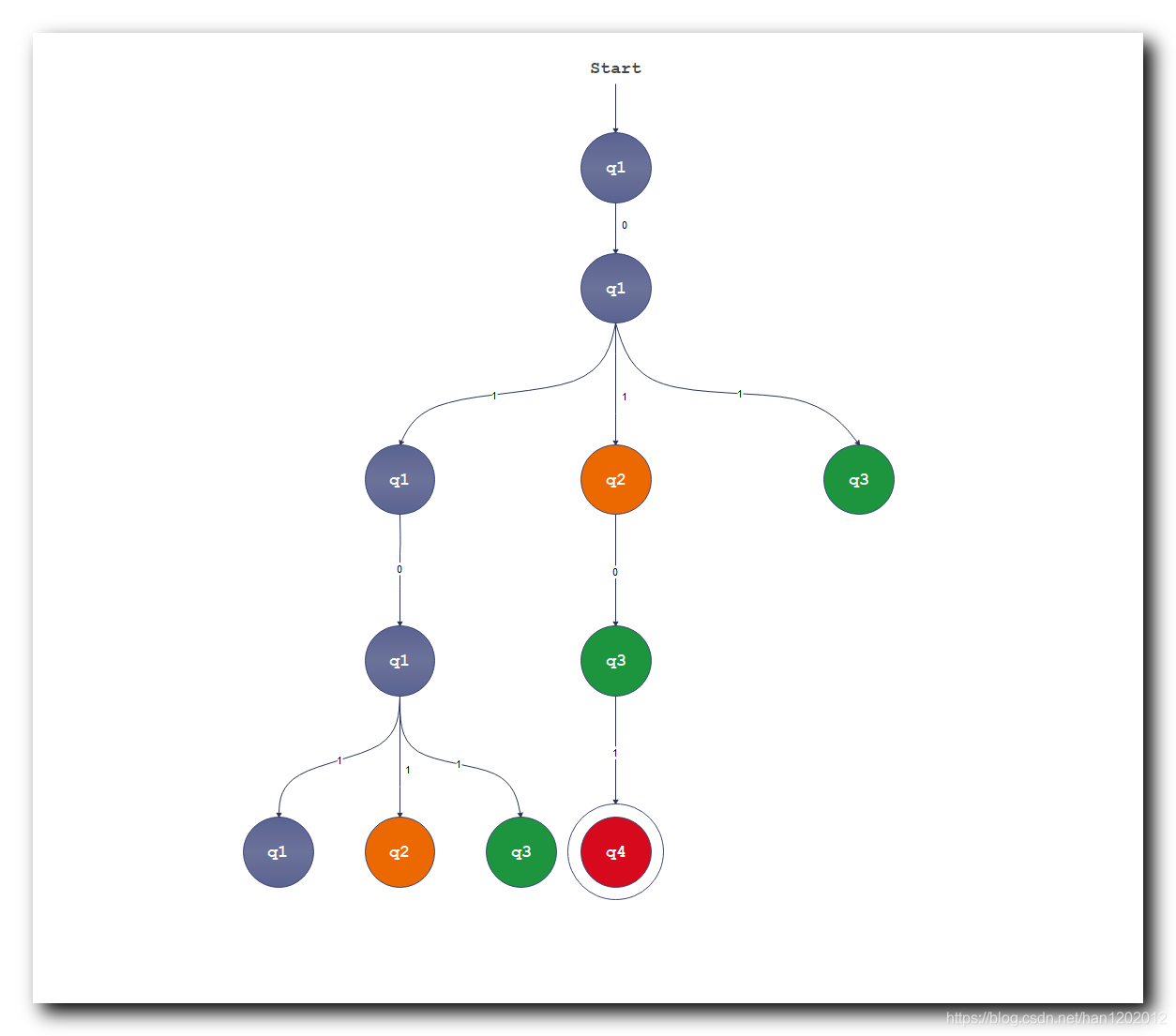
分析第三层的右侧的 q 3 q_3 q3 分支 : 此时输入 0 0 0 字符 , 没有路径 , 该分支终端 ;
这是非确定性自动机最终的计算结果如下图所示 ;
计算树 : 非确定性有限自动机 在 " 0101 0101 0101 " 字符串 上进行计算 , 得到的是一个 计算树 ;
对比 : 确定性自动机计算的时候 , 得到的结果是 链 , 非确定性自动机计算 , 得到的结果是 树 ;
二、判定 非确定性自动机 接受的字符串
如何判定非确定性自动机是否接收某个字符串 ? ? ?
计算结果描述 : 上述的计算树 , 是自动机在 " 0101 0101 0101 " 字符串上的计算 ; 最后一排的状态 q 1 , q 2 , q 3 , q 4 q_1, q_2, q_3, q_4 q1,q2,q3,q4 , 只有 q 4 q_4 q4 是 接受状态 , q 1 , q 2 , q 3 q_1, q_2, q_3 q1,q2,q3 都是 非接受状态 ;
① 接受字符串 : 只要最后一排的叶子结点上 , 存在一个 接受状态 , 那么称 非确定性有限自动机 是 接受这个字符串 " 0101 0101 0101 " 的 ;
② 拒绝字符串 : 如果最后一排的叶子结点上 , 都是 非接受状态 , 那么称 非确定性有限自动机 是 拒绝这个字符串 " 0101 0101 0101 " 的 ;
三、自动机 设计要求
非确定性有限自动机 需求 :
字符集 : Σ = { 0 , 1 } \Sigma = \{0 , 1\} Σ={0,1} ;
语言要求 : 接受的字符串的倒数第三个字符是 1 1 1 ;
分别设计一个确定性有限自动机和非确定性有限自动机 , 对它们进行比较 ;
四、非确定性有限自动机设计
非确定性有限自动机设计思路 : 只要沿着正确的思路设计即可 , 设计出一种正确的自动机即可 ;
自动机启动后 , 自动进入开始状态 q 1 q_1 q1 ;
在开始状态 q 1 q_1 q1 , 接收一个字符 , 假设当前接收的字符已经到了倒数第三个字符 , 是 1 1 1 , 此时满足语言要求 ;
当前时刻后面还可以 输入两个任意字符 , 经历 2 2 2 个任意状态 q 2 , q 3 q_2,q_3 q2,q3 , 最后一个状态 q 4 q_4 q4 是 接受状态 ;
非确定性有限自动机设计如下 :

非确定性有限自动机详细说明 :
① 第一个状态 q 1 q_1 q1 接受 第一个字符 : 其中开始状态是 第一个状态 , 输入 1 1 1 进入第二个状态 , 这个是必须的 , 因为需要倒数第三个字符是 1 1 1 ;
② 第二个状态 q 2 q_2 q2 接受 第二个字符 : 第二个状态 输入不管是 0 0 0 还是 1 1 1 , 都跳转到第三个状态 ;
③ 第三个状态 q 3 q_3 q3 接受 第三个字符 : 第三个状态 输入不管是 0 0 0 还是 1 1 1 , 都跳转到第四个状态 ;
④ 第四个状态 q 4 q_4 q4 接收状态 : 第四个状态是接收状态 , 因为导数第 3 3 3 个字符是 1 1 1 , 该自动机符合要求 ;
第一个状态是导数第三个字符 , 之前还可以有无数个字符 , 可以在 第一个状态下 , 接收任意 0 , 1 0,1 0,1 字符 , 仍然回到第一个状态 ;
上述自动机所接受的字符串 , 刚好是自动机设计要求的字符串 , 倒数第三个字符是 1 1 1 ;
五、非确定性有限自动机 与 确定性 有限自动机 比较
使用非确定性有限自动机 设计上述语言对应的自动机非常方便简洁 , 其远远比确定性有限自动机方便 ;
非确定性有限自动机 与 确定性 有限自动机 比较 :
① 非确定性有限自动机 : 只需要考虑正确的分支即可 , 不需要的分支 , 完全可以不写 ; 如上述要求倒数第三个字符是 1 1 1 , 假如输入的倒数第三个字符是 0 0 0 , 自动机肯定不会接受该字符串 , 非确定性有限自动机中就可以不用考虑这种情况 ;
② 确定性有限自动机 : 但是在确定性有限自动机中 , 必须设计出该分支 , 当导数第三个字符是 0 0 0 的情况 , 需要设计出该分支 , 极大的增加了自动机的复杂性 ;
六、空值转换
ε \varepsilon ε 空字符串在非确定性有限自动机中的 作用 :
开始状态 , 如果读取到 ε \varepsilon ε , 会自动跳转到后续状态 , 这是无条件的条状 , 表示 开始状态 不需要读取任何字符 , 就可以跳转到下一个状态 , 其后续状态 与 开始状态是平级的 ;
使用 ε \varepsilon ε 输入控制转换状态 的操作 , 可以设计自动机可以将设计自动机的语言化整为零 , 将零散设计的自动机组合到一起 , 拼装成一个更大的自动机 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/106128088
- 点赞
- 收藏
- 关注作者


评论(0)