一、 设计自动机 ( 语言要求 )

设计自动机 : 之前是根据给定的自动机 , 找到自动机所能识别的语言 ; 现在是 给定语言 , 设计出能识别该语言的自动机 ;

自动机设计需求 : 设计一个又穷自动机 $M$ , 满足以下的给定的语言要求 ; 即语言已经存在 , 求自动机 ;

1 . 自动机语言字符集 : $\Sigma =\{0,1\}$ , 字符集是 $0$ 和 $1$ 组成 , 该自动机语言由 $0,1$ 组成 , 如 $0101$ , $100111$ 等 ;

2 . 自动机语言描述 :

① 自动机语言集合 : 自动机 $M$ 所能接受的字符串都放在集合 $A$ 中 , 集合 $A$ 就是该自动机语言 ;

② 自动机语言要求 : 自动机 $M$ 的语言 $A$ 集合 中的字符串中都有 奇数 个 $1$ ;

3 . 接受状态 与 非接受状态 : 根据上述自动机语言要求 , 定义接受状态和非接受状态 ;

① 接受状态 : 如果当前输入的字符串中 , 含有奇数个 $1$ 那么当前状态是 接受状态 ;

② 非接受状态 : 如果当前输入字符串中 , 有偶数个 $1$ , 那么当前的状态就是 非接受状态 ;

二、 设计自动机 ( 1 ) 开始状态

Start 开始状态 , 自动机启动后 , 自动跳转到 第一个状态 $S$ ;

三、 设计自动机 ( 2 ) 状态 $S$ 状态类型确定

第一个状态首先要考虑该状态是 接受状态 还是非接受状态 , 如果是接受状态 , 使用双圈表示 , 如果是非接受状态 , 使用单圈表示 ;

先说结论 : 第一个状态 $S$ 是 非接受状态 , 是一个单圈 , 原因如下 :

处于第一个状态时 , 还没有读取任何输入信息 , 当前读取 $0$ 个字符 ;

此时有 $0$ 个 $1$ , $0$ 是偶数 , 也就是当前输入有偶数个 $1$ , 显然不符合语言的要求 ② 必须包含奇数个 $1$ ;

如果当前的状态 , 不符合 自动机语言要求 , 那么需要将当前状态设置成非接受状态 ;

此时的 $S$ 状态就属于此类情况 , 其不符合 $A$ 语言要求 , 有偶数个 $1$ , 因此 $S$ 状态是非接受状态 , 需要使用单圈表示该非接受状态 ;

当前自动机 $M$ 设计 :

四、 设计自动机 ( 3 ) 状态 $S$ 输入输出分析

处于 $S$ 状态时 , 设计自动机的原则是 , 考虑输入任何指令 , 其状态改变 , 即输入 $0$ 指令 , 状态如何改变 , 输入 $1$ 指令 , 状态如何改变 ;

在第一个状态 $S$ 基础上 , 如果输入字符 $0$ , 此时还是有 偶数 个 $1$ , 其要到达的状态还是非接受状态 , 这里将该状态 继续指向 它自己 ; 输入序列 $0$ ;

在第一个状态 $S$ 基础上 , 如果输入字符 $1$ , 此时还是有 奇数 个 $1$ , 此时其要达到一个新的状态 $T$ , 这个新状态 符合 $A$ 语言要求 , 有奇数个 $1$ , 是可接受状态 , 使用双圈表示 ; 输入序列 $1$ ;

当前自动机 $M$ 设计 :

$S$ 状态已经分析完毕 , 下面开始讨论 $T$ 状态的自动机后续设计 ;

五、 设计自动机 ( 4 ) 状态 $T$ 输入输出分析

处于 $T$ 状态时 , 设计自动机的原则是 , 考虑输入任何指令 , 其状态改变 , 即输入 $0$ 指令 , 状态如何改变 , 输入 $1$ 指令 , 状态如何改变 ;

$T$ 状态下 , 如果输入 $0$ , 此时还是有 $1$ 个 $1$ , 即奇数个 $1$ , 其状态还是可接受状态 , 继续指向该状态自己 $T$ ; 输入序列 $00$ ;

$T$ 状态下 , 如果输入 $1$ , 此时输入中出现 $2$ 个 $1$ , 输入了 偶数 个 $1$ , 其状态就是 非接受状态 , 需要 跳转到 非接受状态 $S$ , 箭头从 $T$ 指向 $S$ ; 输入序列 $01$ ;

当前自动机 $M$ 设计 :

六、 最优自动机

自动机性能 : 给定一个 自动机语言 $A$ , 那么根据该语言可以设计出 不同的自动机 , 那么这些自动机之间的性能肯定是不同的 , 有的自动机性能高 , 有的自动机性能低 ;

最优自动机 : 从上述根据 同一个语言 设计出的多个自动机中 , 肯定能选出一个最优自动机 ;

七、 自动机设计算法

自动机生成算法 : 自动机是可以使用算法生成的 , 存在一种算法 , 用该算法生成一个 能识别给定语言的 最优的自动机 ;

八、 确定性 与 非确定性

1 . 确定性 思想 : 自然界一定是确定性的 , 给定一个输入 , 必定对应唯一一个输出 ; 如果出现非确定的输出 , 是由于人的认知有限 , 没有发现其中的未知变量 ; 随着科学认知的发展 , 这些不确定性会消除 ; 以牛顿力学为代表 ;

2 . 非确定性 思想 ( 主流 ) : 自然界是非确定的 , 一个输入对应 不确定 个输出 ; 以量子力学为代表 ;

确定性有穷自动机 的 确定性 , 就是上述确定性思想的应用 ;

下面要将 非确定性思想应用到 自动机设计中 ;

九、 自动机非确定性示例

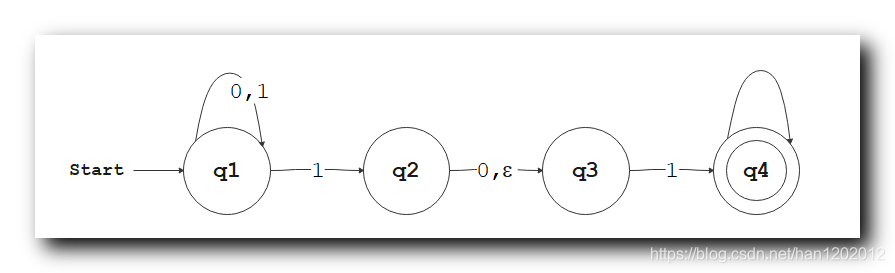
上述 自动机 是一个非确定性自动机 , 非确定性主要体现在以下几个方面 ;

$1$ 个字符输入对应 $2$ 个输出 :

当前状态为 $q_1$ 时 , 读取字符 $1$ 时 , 其后继状态有两个 , 既可以跳转到 $q_1$ 本身状态 , 又可以跳转到 $q_2$ 状态 ;

这个操作是一个非确定性的操作 , 读取一个字符 , 却对应了两个后继状态 ;

$0$ 个字符输入对应 $1$ 个输出 :

当前状态为 $q_2$ 时 , 读取字符 $0$ 或者 $\epsilon$ 空字符串 时 , 就可以跳转到 $q_3$ 状态 ;

$\epsilon$ 表示空字符串 , 其类似于自然数中的 $0$ 的概念 ;

$0$ 个字符输入对应 $0$ 个输出 :

当前状态为 $q_3$ 时 , 为其输入字符 $0$ , 其没有后继状态 ;

这个操作也是一个非确定性操作 , 读取一个字符 , 没有后继状态 ;

自动机中的不确定性 : 不确定性自动机中 , 允许 空字符 或 $1$ 个字符 输入 , 对应 $0$ 个 或 多个输出 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/106084322