一、限制条件的非降路径数

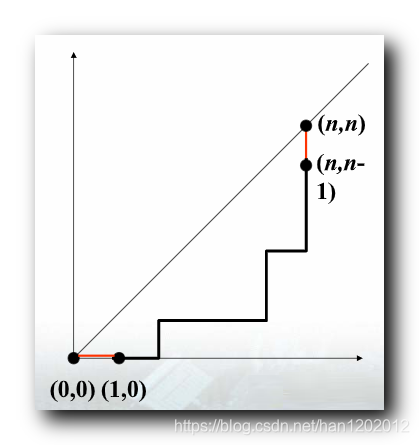
从 $(0,0)$ 到 $(n,n)$ 除端点外 , 不接触对角线的非降路径数 ?

此时无法使用基本公式进行处理了 , 必须使用组合对应的思想 ;

上图示例中 , 从 $(0,0)$ 出发到 $(n,n)$ , 只有两个端点 $(0,0)$ 和 $(n,n)$ 接触了对角线 , 中间的每一步都没有接触该对角线 ;

1 . 计算原理 , 先计算对角线下方的非降路径 : 这里只计数在对角线下方的非降路径数 , 因为 对角线上下的非降路径是对称的 , 因此这里 先将对角线下方的非降路径计算出来 ;

对角线下方的非降路径 乘以 $2$ , 就是总的 不接触对角线的 非降路径数 ;

2 . 出发点分析 : 从 $(0,0)$ 出发后 , 第 $1$ 步必须向右走 , 走到 $(1,0)$ 点 , 如果向上走就不能再下来了 ( 否则就会接触对角线 ) , 此时就不是对角线下方的非降路径了 ;

3 . 终止点分析 :

到达 $(n,n)$ 点 , 只有两种情况 :

• 对角线上方 : 一种情况是从左边 $(n-1,n)$ 到右边的 $(n,n)$ 点 , 该路径在对角线上方 ;
• 对角线下方 : 一种情况是从下边 $(n,n-1)$ 到上边的 $(n,n)$ 点 , 该路径在对角线下方 ;

由于当前只统计 对角线下方的非降路径数 , 到达 $(n,n)$ 之前的一步 , 必须是从 $(n,n-1)$ 位置走到 $(n,n)$ 的 ;

4 . 对应关系

上述 出发点之后必须走 $(1,0)$ 点 , 终点之前必须走 $(n,n-1)$ 点 ,

因此 在对角线下方 从 $(0,0)$ 到 $(n,n)$ 除端点外 , 不接触对角线的非降路径数

等价于

从 $(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数

5 . 计算 $(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数

下面讨论 “从 $(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数” 的计数方式 ;

使用反向思路考虑 , 统计 从 $(1,0)$ 到 $(n,n-1)$ 之间 , 接触过对角线的非降路径 , 剩下的就是不接触对角线的路径 ;

上述两者的总数是 $C(2n-2,n-1)$ 个 ;

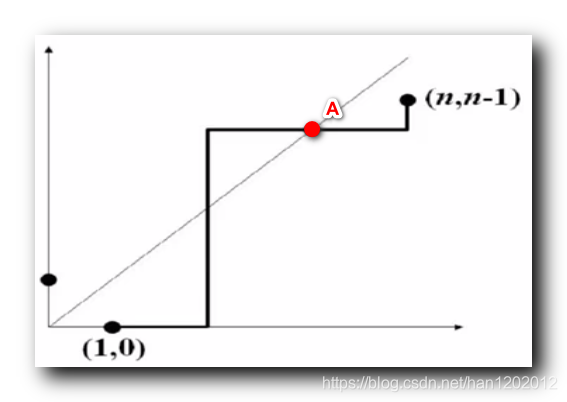
上图是 一个 “从 $(1,0)$ 到 $(n,n-1)$ , 接触过对角线的非降路径” ,

图中的 红色点 $A$ 是该非降路径最后接触对角线的位置 , 前面可能有多次接触该对角线 ;

将 $(1,0)$ 点 与 $A$ 点 之间的蓝色线段 , 关于对角线作对称图像 , 得到 红色线段 ,

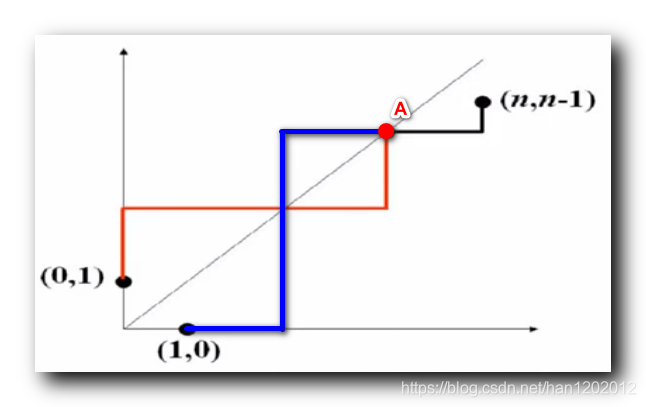
上图中的 蓝色线段 起点是 $(1,0)$ , 那么对应的 红色线段的起点必定是 $(0,1)$ ;

每一条从 $(1,0)$ 开始到 $(n,n-1)$ 的接触对角线的非降路径 , 都有蓝色的线段 , 都可以使用对称的方法 , 得到一个 从 $(0,1)$ 到达 $A$ 点的红色线段 ;

这里就得到了一个组合对应关系 :

每条从 $(0,1)$ 出发 , 到 $(n,n-1)$ 的 非降路径 ( 即将 红色的线段 与 剩余的 黑色线段 可以拼接起来的路径 )

都可以与

从 $(1,0)$ 出发 , 到 $(n,n-1)$ 的接触对角线的 非降路径

一一对应 ;

因此如果要求 "从 $(1,0)$ 出发 , 到 $(n,n-1)$ 的接触对角线的 非降路径数 " , 可以通过求 “从 $(0,1)$ 出发 , 到 $(n,n-1)$ 的 非降路径数” ;

“从 $(0,1)$ 出发 , 到 $(n,n-1)$ 的 非降路径数” 可以使用公式进行计算 , 结果为 $C(2n-2,n)$ ,

对应的 "从 $(1,0)$ 出发 , 到 $(n,n-1)$ 的接触对角线的 非降路径数 " , 结果为 $C(2n-2,n)$ ;

6 . 计算 $(1,0)$ 到 $(n,n-1)$ 的所有非降路径数

根据公式计算即可 , 结果是 : $C(2n-2,n-1)$

7 . 计算 $(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数

"$(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数" 就是

"$(1,0)$ 到 $(n,n-1)$ 的所有非降路径数" 减去 "$(1,0)$ 到 $(n,n-1)$ 除端点外 , 不接触对角线的非降路径数" ;

$C(2n-2,n-1)-C(2n-2,n)$

$=\left(\genfrac{}{}{0ex}{}{2n-2}{n-1}\right)-\left(\genfrac{}{}{0ex}{}{2n-2}{n}\right)$

8 . 计算 从 $(0,0)$ 到 $(n,n)$ 除端点外 , 不接触对角线的非降路径数

上面的 $\left(\genfrac{}{}{0ex}{}{2n-2}{n-1}\right)-\left(\genfrac{}{}{0ex}{}{2n-2}{n}\right)$ 只是计算的是对角线下面的非降路径数 ,

从 $(0,0)$ 出发 , 到 $(n,n)$ 不接触对角线的非降路径数 , 再乘以 $2$ , 就得到了本题目的最终结果 ;

从 $(0,0)$ 到 $(n,n)$ 除端点外 , 不接触对角线的非降路径数

最终结果是 : $2[(\genfrac{}{}{0ex}{}{2n-2}{n-1})-(\genfrac{}{}{0ex}{}{2n-2}{n})]$

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/109191158