一、DSP 知识领域

DSP 领域组成 :

• 信号采集 : A/D 采样 , 抽样定理 , 多抽样率 , 量化噪声分析 ;
• 离散时间信号分析
• 离散时间线性非时变系统
• 信号处理中的快速算法
• 滤波技术
• 信号处理中的特殊算法
• 信号估值
• 信号建模
• 非平稳信号变换

二、抽样定理

A/D 采样中另外一个重要概念是抽样定理 ;

采样中会出现 过采样 ( Nyquist 采样 ) , 欠采样 ( 带通采样 ) 两种情况 ;

• 过采样 ( Nyquist 采样 ) : 采样频率大于等于 $2$ 倍最高频率 ;
• 欠采样 ( 带通采样 ) : 将频率限制在 最高频率 与 最低频率 之间 , 带宽是最高频率减去最低频率值 ;

根据 信号稀疏特性 , 压缩感知原理 , 采样速率 与 信号带宽 无关 , 其取决于 信号中 信息的结构 和 内容 ;

即使带宽很大 , 但是其中信号很少 , 可以使用很低的采样速率将信号进行采样 ;

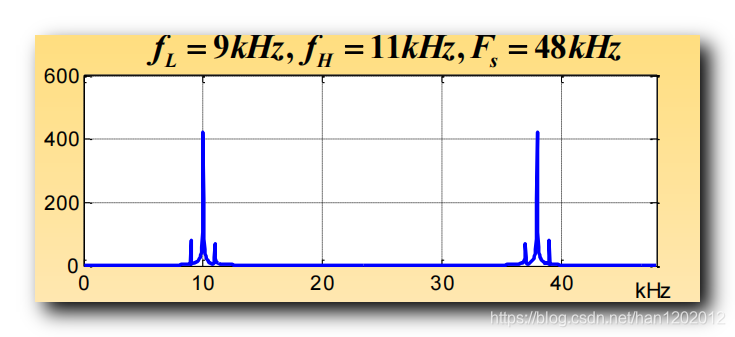
假设一个信号 , 最低频率 $f_L=9kHz$ , 最高频率 $f_H=11kHz$ ,

过采样 ( Nyquist 采样 ) 示例 : 如果使用 $F_s=48kHz$ 的频率进行采样 , 采集的波形图如下 :

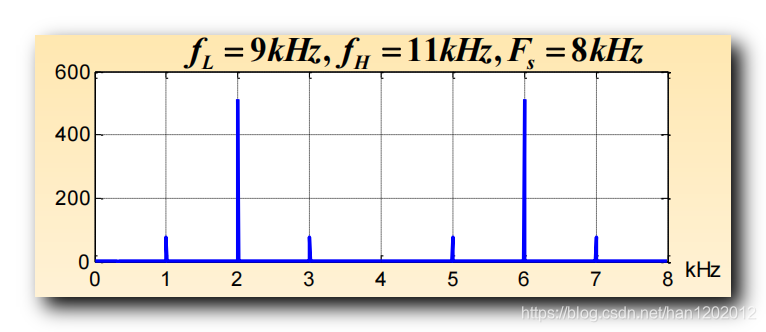
欠采样 ( 带通采样 ) : 如果使用 $F_s=8kHz$ 的频率进行采样 , 采集的波形图如下 :

带宽是 $f_H-f_L=11kHz-9kHz=2kHz$ , 采样频率是带宽的 $4$ 倍 ;

三、多抽样率

多抽样率 : A/D 转换 ( 模拟信号 $\to$ 数字信号 ) 之后 , 可以进行如下操作 ;

• 降采样 : 删除冗余数据 , 降低运算量 ;
• 升采样 : 数字上变频 , 增加采样个数 ;
• 分贝数采样 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/116381882