【集合论】关系闭包 ( 关系闭包相关定理 )
一、关系闭包相关定理 ( 闭包运算不动点 )
R R R 关系是 A A A 集合上的二元关系 , R ⊆ A R \subseteq A R⊆A , 且 A A A 集合不为空集 , A ≠ ∅ A \not= \varnothing A=∅
R R R 关系是自反的 , 当且仅当 R R R 关系的自反闭包 r ( R ) r ( R ) r(R) 也是 R R R 关系本身 ;
R 自 反 ⇔ r ( R ) = R R 自反 \Leftrightarrow r(R) = R R自反⇔r(R)=R
R R R 关系是对称的 , 当且仅当 R R R 关系的对称闭包 s ( R ) s ( R ) s(R) 也是 R R R 关系本身 ;
R 对 称 ⇔ s ( R ) = R R 对称 \Leftrightarrow s(R) = R R对称⇔s(R)=R
R R R 关系是传递的 , 当且仅当 R R R 关系的传递闭包 t ( R ) t ( R ) t(R) 也是 R R R 关系本身 ;
R 传 递 ⇔ t ( R ) = R R 传递 \Leftrightarrow t(R) = R R传递⇔t(R)=R
二、关系闭包相关定理 ( 闭包运算单调性 )
R 1 , R 2 R_1 , R_2 R1,R2 关系是 A A A 集合上的二元关系 , R 2 R_2 R2 关系包含 R 1 R_1 R1 关系 , R 1 ⊆ R 2 ⊆ A × A R_1 \subseteq R_2 \subseteq A \times A R1⊆R2⊆A×A , 且 A A A 集合不为空集 , A ≠ ∅ A \not= \varnothing A=∅
R 1 R_1 R1 关系的自反闭包 包含于 R 2 R_2 R2 关系的自反闭包
r ( R 1 ) ⊆ r ( R 2 ) r(R_1) \subseteq r(R_2) r(R1)⊆r(R2)
R 1 R_1 R1 关系的对称闭包 包含于 R 2 R_2 R2 关系的对称闭包
s ( R 1 ) ⊆ s ( R 2 ) s(R_1) \subseteq s(R_2) s(R1)⊆s(R2)
R 1 R_1 R1 关系的传递闭包 包含于 R 2 R_2 R2 关系的传递闭包
t ( R 1 ) ⊆ t ( R 2 ) t(R_1) \subseteq t(R_2) t(R1)⊆t(R2)
三、关系闭包相关定理 ( 闭包运算与并运算之间的关系 )
R 1 , R 2 R_1 , R_2 R1,R2 关系是 A A A 集合上的二元关系 , R 2 R_2 R2 关系包含 R 1 R_1 R1 关系 , R 1 ⊆ R 2 ⊆ A × A R_1 \subseteq R_2 \subseteq A \times A R1⊆R2⊆A×A , 且 A A A 集合不为空集 , A ≠ ∅ A \not= \varnothing A=∅
自反闭包并集 : R 1 R_1 R1 关系 与 R 2 R_2 R2 关系 并集 的 自反闭包 , 等于 R 1 R_1 R1 关系的自反闭包 与 R 2 R_2 R2 关系的自反闭包 的并集 ;
r ( R 1 ∪ R 2 ) = r ( R 1 ) ∪ r ( R 2 ) r(R_1 \cup R_2) = r(R_1) \cup r(R_2) r(R1∪R2)=r(R1)∪r(R2)
对称闭包并集 : R 1 R_1 R1 关系 与 R 2 R_2 R2 关系 并集 的 对称闭包 , 等于 R 1 R_1 R1 关系的对称闭包 与 R 2 R_2 R2 关系的对称闭包 的并集 ;
s ( R 1 ∪ R 2 ) = s ( R 1 ) ∪ s ( R 2 ) s(R_1 \cup R_2) = s(R_1) \cup s(R_2) s(R1∪R2)=s(R1)∪s(R2)
传递闭包并集 : R 1 R_1 R1 关系 与 R 2 R_2 R2 关系 并集 的 传递闭包 , 包含 R 1 R_1 R1 关系的传递闭包 与 R 2 R_2 R2 关系的传递闭包 的并集 ;
t ( R 1 ∪ R 2 ) ⊇ t ( R 1 ) ∪ t ( R 2 ) t(R_1 \cup R_2) \supseteq t(R_1) \cup t(R_2) t(R1∪R2)⊇t(R1)∪t(R2)
四、传递闭包并集反例
传递闭包 的反例 :
集合 A = { a , b } A = \{a, b\} A={a,b}
关系 R 1 = { < a , b > } R_1 = \{ <a,b> \} R1={<a,b>} , 关系 R 2 = { < b , a > } R_2 = \{ <b,a> \} R2={<b,a>}
R 1 R_1 R1 关系的传递闭包 : t ( R 1 ) = { < a , b > } t(R_1) = \{ <a,b> \} t(R1)={<a,b>}

R 2 R_2 R2 关系的传递闭包 : t ( R 2 ) = { < b , a > } t(R_2) = \{ <b,a> \} t(R2)={<b,a>}
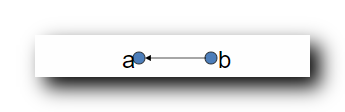
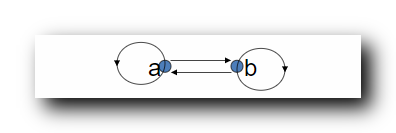
并集的闭包 : t ( R 1 ∪ R 2 ) = { < a , b > , < a , a > , < b , a > , < b , b > } t(R_1 \cup R_2) = \{ <a,b> , <a,a> , <b,a> , <b,b> \} t(R1∪R2)={<a,b>,<a,a>,<b,a>,<b,b>}
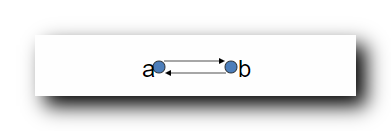
闭包的并集 : t ( R 1 ) ∪ t ( R 2 ) = { < a , b > , < b , a > } t(R_1) \cup t(R_2) = \{ <a,b> , <b, a> \} t(R1)∪t(R2)={<a,b>,<b,a>} , 该关系是非传递的 ;
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/108957697
- 点赞
- 收藏
- 关注作者


评论(0)