一、自反性

自反性符号描述 :

$R\subseteq A\times A$

$R$ 关系是 自反的

$\iff$

$\forall x(x\in A\to xRx)$

$\iff$

$(\forall x\in A)xRx$

非自反性符号描述 :

$R$ 是非自反的 $\iff$ $\exists x(x\in A\wedge \neg xRx)$

自反性文字描述 :

$R$ 是 $A$ 集合上的二元关系 ,

$R$ 是自反的 ,

当且仅当 $R$ 集合中的 , 任意 $x$ 属于集合 $A$ 的元素 , $x$ 与 $x$ 都有关系 $R$ ( 必须是所有的 $x$ )

非自反 文字描述 : 存在 $x$ 元素 , $x$ 属于 $A$ 集合中的元素 , 并且 $x$ 与 $x$ 没有关系 ;

自反性 是验证 每个元素 与其本身 都有 $R$ 关系

非自反性 只要有一个元素 与其本身 没有 $R$ 关系就成立

$\varnothing$ 上的空关系 , 既是自反的 , 又是反自反的

二、自反性定理

自反性定理 :

$R$ 是自反的

$\iff$

$I_A\subseteq R$

$\iff$

$R^{-1}是自反的$

$\iff$

$M(R)$ 关系矩阵主对角线上的值都为 $1$

$\iff$

$G(R)$ 关系图中每个顶点都有环

文字描述 :

$R$ 是自反的

当且仅当 $R$ 包含恒等关系 , $I_A\subseteq R$

当且仅当 $R^{-1}$ 是自反的

当且仅当 $M(R)$ 关系矩阵主对角线上的元素全部是 $1$

当且仅当 $G(R)$ 关系图中每个顶点均有环

三、反自反性

反自反性 :

$R\subseteq A\times A$

$R$ 是反自反的

$\iff$

$\forall x(x\in A\to \neg xRx)$

$\iff$

$(\forall x\in A)\neg xRx$

关系图 :

自反 是每个点 都有环 ( 重点 )

非自反 是 有的有环 , 有的没有环

反自反 是每个点 都没有环 ( 重点 )

非反自反 是 有的有环 , 有的没有环

$\varnothing$ 上的空关系 , 既是自反的 , 又是反自反的

四、反自反性定理

反自反定理 :

$R$ 是反自反的

$\iff$

$I_A\cap R=\varnothing$

$\iff$

$R^{-1}$ 是反自反的

$\iff$

$M(R)$ 主对角线上的元素都为 $0$

$\iff$

$G(R)$ 每个顶点处都没有环

文字描述 :

$R$ 是反自反的

当且仅当 关系 $R$ 与 恒等关系 $I_A$ 不相交

当且仅当 关系的逆 $R^{-1}$ 是反自反的

当且仅当 关系矩阵 $M(R)$ 主对角线上的元素全部为 $0$

当且仅当 关系图 $G(R)$ 的每个顶点都没有环

五、自反与反自反示例

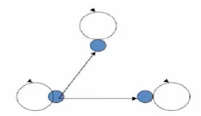
上述关系图中 , 每个顶点都有环 , 是自反的 ;

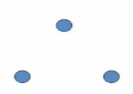
上述关系图中 , 每个顶点都没有环 , 是反自反的

上述关系图中 , 有的顶点有环 , 有的顶点没有环 , 什么都不是 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/108916590