参考博客 :

• 【计算理论】上下文无关语法 ( 语法组成 | 规则 | 语法 | 语法示例 | 约定的简写形式 | 语法分析树 )
• 【计算理论】上下文无关语法 ( 代数表达式 | 代数表达式示例 | 确定性有限自动机 DFA 转为 上下文无关语法 )
• 【计算理论】上下文无关语法 CFG ( CFG 设计示例 | CFG 歧义性 | Chomsky 范式 | 上下文无关语法 转为 Chomsky 范式 )

一、上下文无关文法 ( CFG )

上下文无关语法 组成 : 由 $\{V,\Sigma ,R,S\}$ 四部分组成 ;

变量集 $V$ : 有限的变量集合 ;

终端字符集 $\Sigma$ : 有限的终端字符组成的集合 ; 相当于常量的含义 , 与变量相对 ;

规则集 $R$ : 有限的规则组成的集合 , 规则规定如何进行代换操作 , 规定 变量 , 终端字符 , 字符串变量 等 ;

开始变量 $S$ : 该变量作为开始变量 ;

规则 :

① 已知条件 : 假设 $u,v,w$ 是 变量 ( 变元 ) 或 终端字符集 ( 常量 / 常元 ) ;

② 规则描述 : 规则是一个箭头 , $A\to w$ , $A$ 是变元 , $w$ 是 变元 和 常元 组成的终端字符 ;

③ 规则用法 : 在字符串中 , 根据 $A\to w$ 规则进行替换 , 只需要将 $A$ 变元替换成 $w$ 字符串即可 ;

④ 规则示例 : $uAv$ 中使用上述规则进行替换 , 将 $A$ 替换成 $w$ , 替换结果是得到新字符串 $uwv$ ;

$$uAv\Rightarrow uwv$$

二、上下文无关文法 ( CFG ) 示例

上下文无关文法 ( CFG ) : $\mathrm{G}3=(\{\mathrm{S}\},\{\mathrm{a},\mathrm{b}\},\mathrm{R},\mathrm{S})$ 其组成如下 :

• 变量集 $\{\mathrm{S}\}$ ;

• 终端字符集 $\{\mathrm{a},\mathrm{b}\}$ ;

• 规则 $\mathrm{R}$ ;

• 开始变量 $\mathrm{S}$ ;

规则 $\mathrm{R}$ 描述 : $\mathrm{S}\to \mathrm{a}\mathrm{S}\mathrm{b}|\mathrm{S}\mathrm{S}|\epsilon$

• $\mathrm{S}$ 变量 可以使用 $\mathrm{a}\mathrm{S}\mathrm{b}$ 字符串替换 ;
• $\mathrm{S}$ 变量 可以使用 $\mathrm{S}\mathrm{S}$ 字符串替换 ;
• $\mathrm{S}$ 变量 可以使用 $\epsilon$ 字符串替换 ;

规则替换过程 : 下面的 ① ~ ⑦ 分别对应七次规则替换 ;

$\mathrm{S}\Rightarrow \mathrm{a}\mathrm{S}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{S}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{b}$

• ① $\mathrm{S}\mathrm{S}$ 是开始变量 , 可以使用 $\mathrm{a}\mathrm{S}\mathrm{b}$ 替换 $\mathrm{S}$ ; $\mathrm{S}\Rightarrow \mathrm{a}\mathrm{S}\mathrm{b}$
• ② 使用 $\mathrm{a}\mathrm{S}\mathrm{b}$ 替换 $\mathrm{S}$ ; $\mathrm{a}\mathrm{S}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}$
• ③ 使用 $\mathrm{S}\mathrm{S}$ 替换 $\mathrm{S}$ ; $\mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{S}\mathrm{S}\mathrm{b}\mathrm{b}$
• ④ 使用 $\mathrm{a}\mathrm{S}\mathrm{b}$ 替换第一个 $\mathrm{S}$ ; $\mathrm{a}\mathrm{a}\mathrm{S}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}$
• ⑤ 使用 $\epsilon$ 替换第一个 $\mathrm{S}$ ; $\mathrm{a}\mathrm{a}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}$
• ⑥ 使用 $\mathrm{a}\mathrm{S}\mathrm{b}$ 替换 $\mathrm{S}$ ; $\mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{S}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}\mathrm{b}$
• ⑦ 使用 $\epsilon$ 替换 $\mathrm{S}$ ; $\mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{S}\mathrm{b}\mathrm{b}\mathrm{b}\Rightarrow \mathrm{a}\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{b}$

三、确定性有限自动机 DFA 转为 上下文无关语法 CFG

1 . 确定性有限自动机 ( DFA ) 转为 上下文无关语法 ( CFG ) : 将

确定性有限自动机 ( DFA ) 的指令 , 转为 对应的

上下文无关语法 ( CFG ) 规则 : $\delta ({\mathrm{q}}_{\mathrm{i}},\mathrm{a})={\mathrm{q}}_{\mathrm{j}}\Rightarrow {\mathrm{R}}_{\mathrm{i}}\to \mathrm{a}{\mathrm{R}}_{\mathrm{j}}$

$\delta (q_i,a)=q_j$ 表示 $q_i$ 状态下 , 读取字符 $a$ , 跳转到 $q_j$ 状态 ;

2 . 自动机的 状态跳转 转换成 规则 示例 : 下图中的 确定性有限自动机 , 开始状态 $A$ 读取 $1$ 字符 转化成 $B$ 状态 , 表示成规则就是 $R_A\to 1R_B$

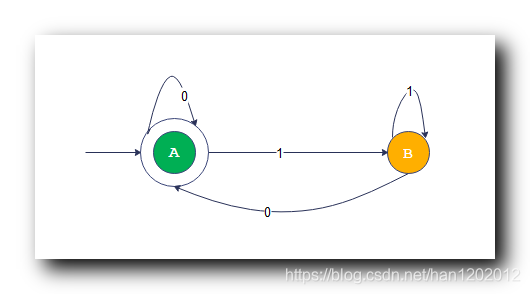
3 . 自动机的状态 $A$ 读取 字符 $a$ 转换成另一个状态 $B$ , 都可以转换成对应的规则 $R_A\to a{R}_B$ ;

4 . 计算能力对比 : 上下文无关语法 的计算能力 要大于等于 自动机的计算能力 ;

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/111402658