吴恩达老师机器学习笔记(一:基础部分)
吴恩达老师机器学习视频课程笔记简记
- 1
第一章
- 课时1:
| 类型 | 应用场景 |
|---|---|
| 数据挖掘 | 用户点击次数统计,用户画像 |
| 手写体数字识别 | 信封邮编识别 |
| 个性化推荐 | 销售产品,音视频推荐 |
- 课时2:
机器学习的定义
| 案例 | 成果 |
|---|---|
| 跳棋 | 计算机下跳棋不断战胜新的对手 |
| 邮件过滤 | 智能分类邮件是否是垃圾邮件 |
| 监督学习 | 我们教会计算机做某件事情 |
| 无监督学习 | 我们让计算机自己学习 |
- 课时3:
定义监督学习:数据集是有标注的数据样本,对新的样本数据做预测
分类问题:预测新数据类别,离散值
二分类和多分类
回归问题:预测值可以看作是连续的,输出是数值的问题是回归
分类和回归都是有监督学习
| 案例 | 类别 |
|---|---|
| 房价预测 | 回归 |
| 商品销量 | 回归 |
| 邮件分类 | 分类 |
| 肿瘤良性预测 | 分类 |
| 软件判断客户账户是否被入侵 | 分类 |
- 课时4:
非监督学习:样本数据没有对应标签,目标是发现输入数据中的规律、结构特征
| 案例 | 类别 |
|---|---|
| 谷歌新闻 | 聚类算法 |
| DNA 人种分类 | 聚类算法 |
| 计算机集群 | 聚类算法 |
| 社交网络分析 圈子分析 | 聚类算法 |
| 市场客户分类 | 聚类算法 |
| 天文数据分析 | 聚类算法 |
第二章
- 课时6:
| 案例 | 类别 | 描述 |
|---|---|---|
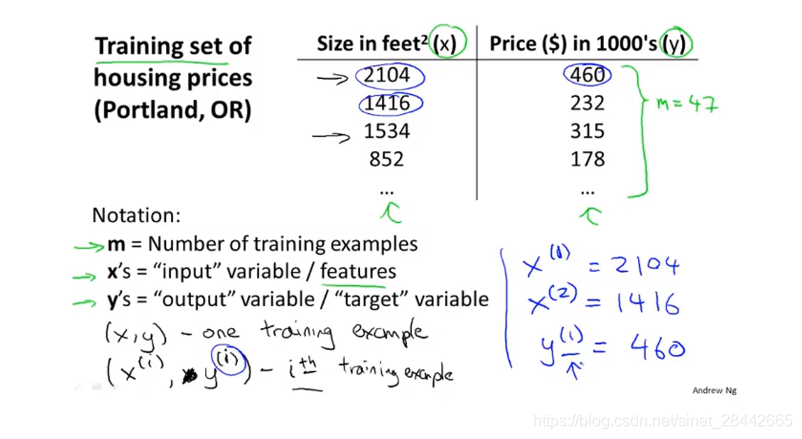
| 房价预测 | 监督学习:回归 | 数据:房子大小和房价 |
| 肿瘤判断 | 监督学习:分类 | 数据:只有0和1两种结果 |
-
课时7:
代价函数:
平方误差代价函数

-
课时10:
梯度下降:

同时更新参数

-
课时11:
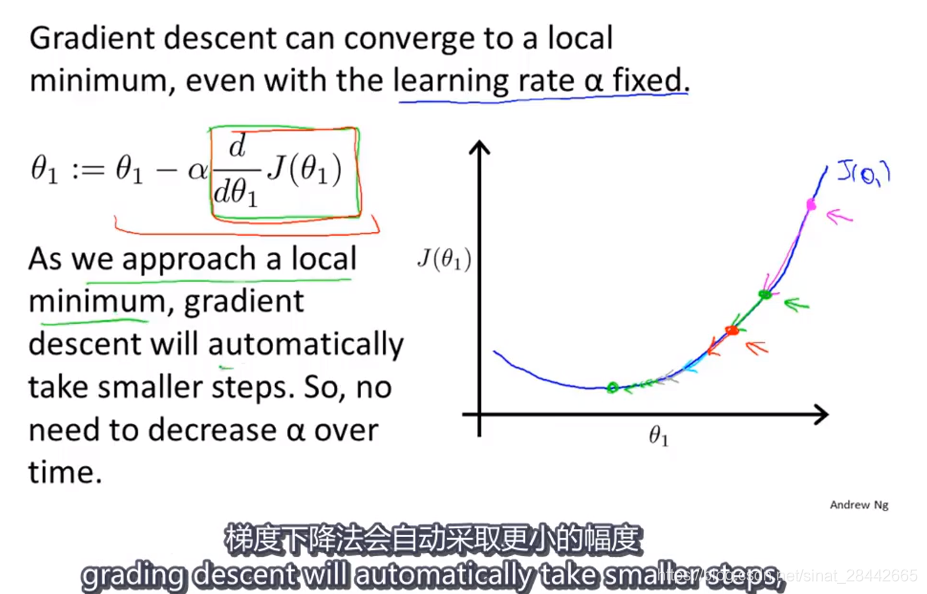
梯度下降

倒数变小,学习率变小,找到局部最优

-
课时12:
批量梯度下降 Batch Gradient Descent 每一步梯度下降

第三章——线性代数回顾 :略过
第四章——Matlab和Octave两个软件的安装:略过
第五章——多变量线性回归
课时28:
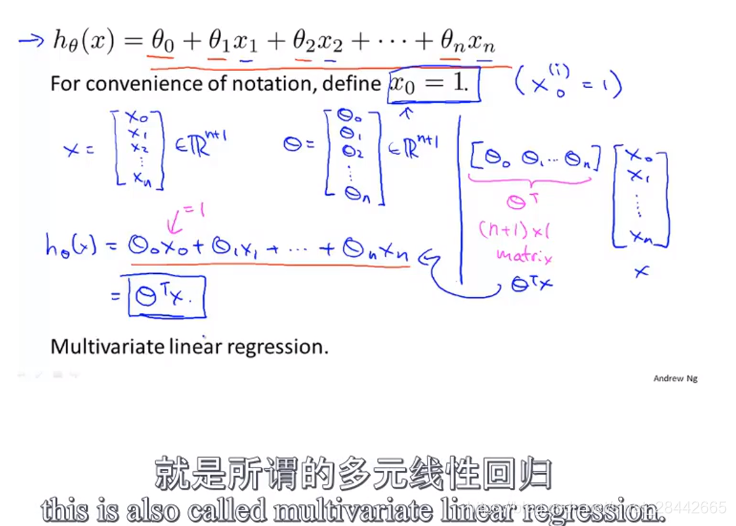
使用多个特征变量来预测y
课时29:多元梯度下降
课时30:
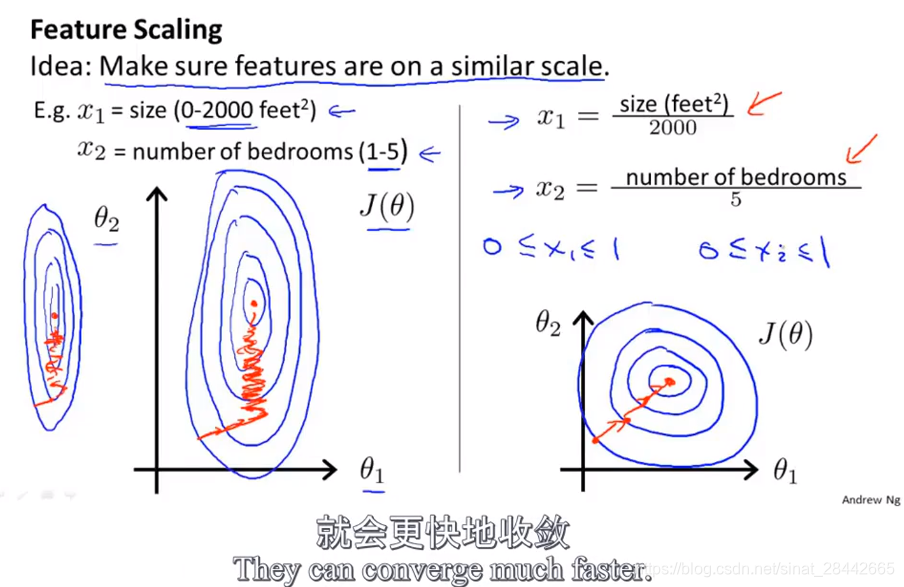
特征缩放:
Mean normalization 均值 归一化:
房子的size在0-2000之间,归一化:
x1 = (size - 1000) / 2000
即:减去平均值,除以其特征范围, 则特征值归一化到 [ -0.5, 0.5 ] 之间
所有的特征都做 归一化,则 可以加快 梯度下降的速度
公式为:
x1 = ( x1 - u1 ) / s1 , x1 是第一个特征向量,u1是其平均值,s1 是其特征范围, 最大值 - 最小值 的值 或者 标准差
特征缩放,不需要非常精确,只是为了让梯度下降 得更快一点,这样收敛迭代的次数更少
所有的特征都取值在近似的范围,这样梯度下降就可以更快地收敛
原因如下:
两个特征为例:
左图,房间size和卧室数量,比例相差非常大,整体是椭圆,收敛速度很慢,归一化之后,代价函数等值线呈现圆形,进而加快收敛。
推广到多个特征,是一样的道理
课时31:
学习率
梯度下降的学习率
梯度下降算法所做的事情:就是为你找到一个Θ值,并且希望它能够最小化代价函数J(Θ)
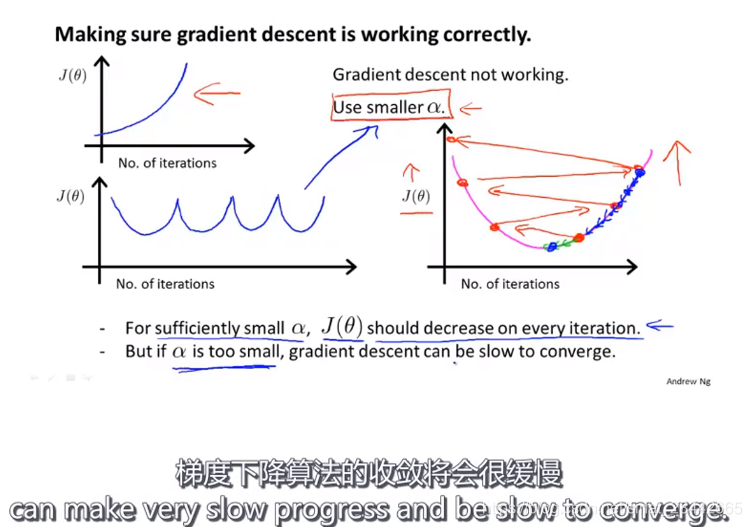
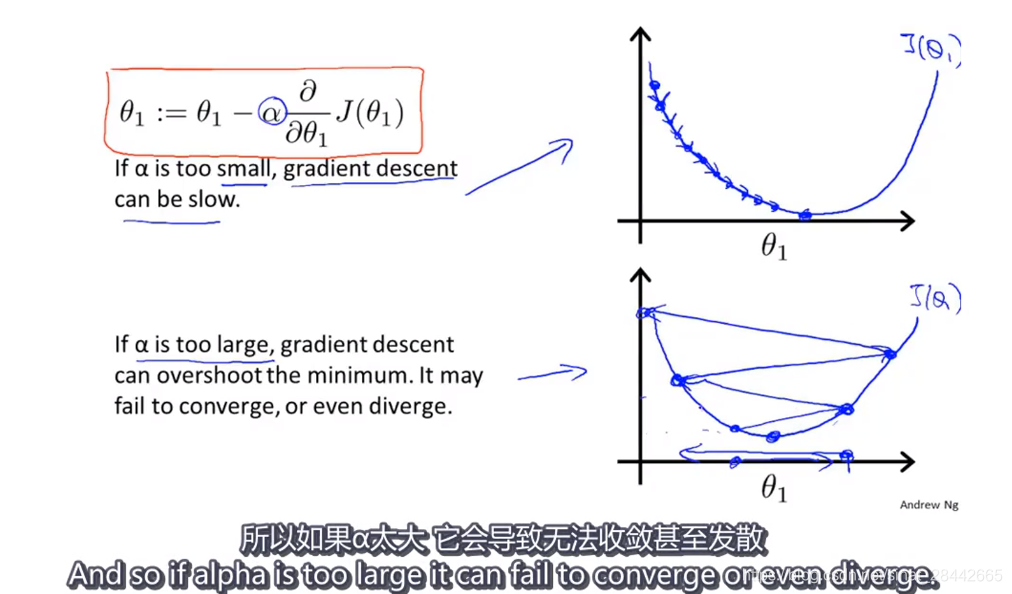
如果梯度下降算法正常工作的话,每一步迭代之后J(Θ)都应该下降。
数学家已经证明,只要学习率足够小,则正常情况下,每次迭代,代价函数J(Θ)都会变小。
如果迭代次数增加,J(Θ)反而上升,原因:学习率太大了
学习率太小:收敛速度很慢,所以要找到一个合适的学习率
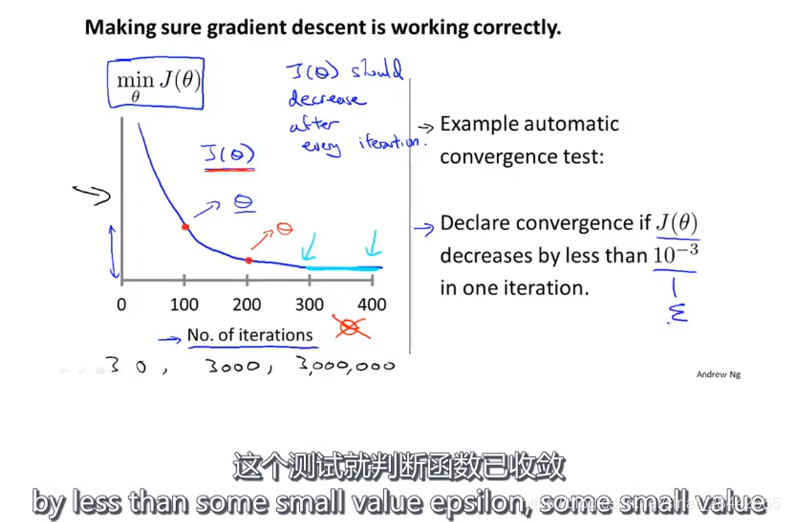
吴恩达老师,找合适学习率方法:学习率每次扩大3倍,我们也可以扩大10倍,
找到一个太小的值和另一个太大的值,然后取最大可能值,或者比最大值略小一些的——合适的学习率
找到适合的学习率的方法:
吴恩达老师做法:观察最小代价函数随着梯度下降迭代次数增加的变化曲线,来判断梯度下降算法是否已经收敛
通常的判断是否收敛方法是:设定阈值,如果 代价函数J(Θ) 下降区间 小于 10^-3 则说明其收敛,
但阈值并不是特别好确定。

课时32:
选择合适的特征,如房价:房屋长和宽可以看作是房屋面积,通过定义新的特征,可能会得到一个更好的模型。
数据特征非常多时,我们要选择重要的特征,一些算法可以自动选择需要使用的特征,用多项式函数来拟合特征。

课时33:
正规方程:可以直接通过求导,求得导函数为0 的点或者说使偏导数为0,即可找到代价函数极值,进而找到最小值

向量x0的值都是1
正规方程与梯度下降的有点和缺点:

对于吴恩达老师而言:只要特征变量n的数目并不大,正规方程是一个很好的计算参数Θ的方法,
只要n小于10000,对于线性回归这个特定的模型,通常使用正规方程法,
当特征个数n超过10000时,会考虑尝试梯度下降或者其他算法,
课时34:
矩阵不可逆出现的情况:
两个特征表示同一个情况,或者特征太多 ,多于样本个数
文章来源: positive.blog.csdn.net,作者:墨理学AI,版权归原作者所有,如需转载,请联系作者。
原文链接:positive.blog.csdn.net/article/details/85881797
- 点赞
- 收藏
- 关注作者




评论(0)