【数据挖掘】数据挖掘总结 ( 数据挖掘相关概念 ) ★★
一、 数据挖掘特点
1 . 用于挖掘的数数据源 必须 真实 :
① 存在的真实数据 : 数据挖掘处理的数据一般是存在的真实数据 , 不是专门收集的数据 ;
② 数据收集 : 该工作不属于数据挖掘范畴 , 属于统计任务 ;
2 . 数据必须海量 :
① 少量数据处理 : 少量数据使用统计方法分析 , 不必使用数据挖掘 ;
② 海量数据 : 处理海量数据时 , 才使用数据挖掘 , 涉及到 有效存储 , 快速访问 , 合理表示 等方面的问题 ;
3 . 数据挖掘的查询是随机的 : 决策者 ( 用户 ) 提出的随机查询 ;
① 要求不精确 : 查询灵活 , 没有精确的要求 ( 无法用 SQL 语句写出来 ) ;
② 结果正确性未知 : 查询出来结果也不知道是否准确 ;
4 . 未知结果 :
① 挖掘结果 : 数据挖掘 挖掘出的知识是未知的 , 目的是为了发掘潜在的知识 , 模式 ; 这些知识只能在特定环境下可以接收 , 可以理解 , 可以运用 ;
② 知识使用 : 数据挖掘出的知识只能在特定领域使用 , 如金融领域数据挖掘结果 , 只能在金融领域及相关领域使用 ;
参考博客 :
二、 数据挖掘组件化思想
0 . 数据挖掘算法的五个标准组件 :
- ① 模型或模式结构 : 决策树模型 , ( 信念 ) 贝叶斯模型 , 神经网络模型 等 ;
- ② 数据挖掘任务 : 概念描述 , 关联分析 , 分类 , 聚类 , 异常检测 , 趋势分析 等 ;
- ③ 评分函数 : 误差平方和 , 最大似然 , 准确率 等 ;
- ④ 搜索和优化方法 : 随机梯度下降 ;
- ⑤ 数据管理策略 : 数据存储 , 数据库相关 ;
1 . 模型或模式结构 : 通过 数据挖掘过程 得到知识 ; 是算法的输出格式 , 使用 模型 / 模式 将其表达出来, 如 : 线性回归模型 , 层次聚类模型 , 频繁序列模式 等 ;
2 . 数据挖掘任务分类 : 根据数据挖掘的目标 , 可以将数据挖掘任务分为以下几类 : ① 模式挖掘 , ② 描述建模 , ③ 预测建模 ;
描述建模 和 预测建模 又称为 模型挖掘 ;
① 模式挖掘 : 如 异常模式 , 频繁模式 ;
② 描述建模 : 如 聚类分析 ;
③ 预测建模 : 如 分类预测 , 趋势分析等 ;
3 . 评分函数 : 常用的评分函数有 似然函数 , 误差平方和 , 准确率等 ;
① 评分函数概念 : 评分函数用于评估 数据集 与 模型 ( 模式 ) 的拟合程度 , 值 越大 ( 越小 ) 越好 ;
② 评分函数作用 : 为 模型 ( 模式 ) 选出最合适的参数值 ;
4 . 搜索和优化算法作用 : 确定 模型 ( 模式 ) 以及其相关的 参数值 , 该模型 ( 模式 ) 使评分函数 达到某个最大 ( 最小 ) 值 ; 本质是帮助评分函数取得 最大 ( 最小 ) 值的方法 ;
① 结构确定求参数 ( 优化问题 ) : 模型 ( 模式 ) 结构确定后 , 目的就是为了确定参数值 , 针对固定的 模式 ( 模型 ) 结构 , 确定一组参数值 , 使评分函数最优 , 这是优化问题 ;
② 结构不确定 ( 搜索问题 ) : 搜索 既需要确定 模型 ( 模式 ) 的结构 , 又需要确定其参数值 , 这种类型是搜索问题 ;
5 . 数据管理策略 : 传统数据与大数据 ; 设计有效的数据组织与索引技术 , 通过采样 , 近似等手段 , 减少扫描次数 , 提高数据挖掘算法效率 ;
① 传统数据 ( 内存管理数据 ) : 传统的数据管理方法是将数据都放入内存中 , 少量数据 , 直接在内存中处理 , 不需要特别关注数据管理技术 ;
② 大数据 ( 集群管理数据 ) : 数据挖掘中的数据一般是 GB , TB 甚至 PB 级别的大数据 , 如果使用传统的内存算法处理这些数据 , 性能会很低 ;
确定 模型 / 模式 结构 和 评分函数 , 是人来完成 , 优化评分函数的过程是计算机完成 ;
参考博客 :
- 【数据挖掘】数据挖掘算法 组件化思想 ( 模型或模式结构 | 数据挖掘任务 | 评分函数 | 搜索和优化算法 | 数据管理策略 )
- 【数据挖掘】数据挖掘算法 组件化思想 示例分析 ( 组件化思想 | Apriori 算法 | K-means 算法 | ID3 算法 )
三、 朴素贝叶斯 与 贝叶斯信念网络
朴素贝叶斯算法是朴素的 , 是因为在 分类的计算 过程中 , 做了一个 朴素的假设 , 假定 属性值之间是相互独立的 , 该假设称作 条件独立 , 做此假设的目的是为了简化计算 ;
( 教科书上的标准描述 )
四、 决策树构造方法
递归 : 从 根节点 开始 , 从上到下递归 ;
分治 : 采用 分而治之 的方法 , 通过不断 将 训练样本 划分成子集 , 构造决策树 ;
递归过程 : 训练集 T \rm T T 有 A \rm A A 个变量 , Y \rm Y Y 个类别 , 针对 T \rm T T 构造决策树 , 出现以下情况 :
① 类别相同 ( 递归停止条件 ) : 如果 T \rm T T 中 样本类别相同 , 决策树只有一个叶子结点 ;
② 属性用尽 ( 递归停止条件 ) : 如果 T \rm T T 没有用于继续分裂的变量 , 则将 T \rm T T 中出现频率最高的类别作为当前节点的类别 ;
③ 样本用尽 ( 递归停止条件 ) : 如果 T \rm T T 中的样本都分配完毕 , 现在为空 , 则停止递归 ;
④ 分支 ( 递归操作 ) : 如果 T \rm T T 包含的样本属于不同类别 , 根据变量选择策略 , 选择最佳的 变量 和 划分方式 , 将 T \rm T T 分为多个子集 , 每个子集构成一个内部结点 ;
针对上述每个内部结点 , 都进行上述 ① ② ③ ④ 递归操作 , 直到满足决策树的终止条件为止 ;
递归终止条件 :
① 类别相同 : 样本所有结点对应的样本 都属于同一个类别 ;
② 属性用尽 : T \rm T T 中 没有可进一步分裂的变量 ;
③ 样本用尽 : T \rm T T 中的样本为空 ;
决策树构建算法 : Generate_Decision_Tree
输入 : 训练集 T \rm T T , 变量集 A \rm A A , 类别 Y \rm Y Y
输出 : 决策树 T r e e \rm Tree Tree
Generate_Decision_Tree ( T , A , Y )
① 样本用完 : 如果 T \rm T T 为空 , 返回错误信息 ; ( 递归停止条件 )
② 类型相同 : 如果 T \rm T T 所有样本都属于类别 C \rm C C , 则 C \rm C C 类型就是当前结点类型 , 返回 ; ( 递归停止条件 )
③ 属性用尽 : 如果 T \rm T T 的所有变量属性都被使用了 , 则使用出现频率最高的类别作为本结点的类型 , 返回 ; ( 递归停止条件 )
④ 生成分支 : 根据 变量选择策略 选择最佳变量 X \rm X X 将 训练集 T \rm T T 分为多个子集 ;
⑤ 标识根节点 : 使用 X \rm X X 标识当前结点 ;
⑥ 递归操作 : 对 ④ 中分割的多个子集执行 Generate_Decision_Tree 递归操作 , X \rm X X 结点指向 这些递归操作生成的新的分支 ;
⑦ 返回当前的结点 ;
五、 K-Means 算法优缺点
K-Means 算法优点 :
① 处理大数据量有 可扩充性 和 高效率 ; 其算法复杂度是 O ( t k n ) \rm O(tkn) O(tkn) , n \rm n n 是样本个数 , k \rm k k 是聚类个数 , t \rm t t 是循环次数 ;
② 可以实现局部最优化 ;
K-Means 算法缺点 :
① 族个数 : 族的个数 K \rm K K 必须事先确定 ;
② 形状 : 无法找到 特殊形状 的族 , 如凹形的 ;
③ 异常值 : 对于 异常数据敏感 , 异常数据对中心点计算影响很大 ;
④ 必须给定 K \rm K K 个初始中心点 , 中心点选不好 , 影响聚类质量 ;
⑤ 求中心点时 , 需要计算算术平均值 , 针对分类属性的数据无法计算 , 如男女无法计算 ;
六、 DBSCAN 算法优缺点
DBSCAN 算法优点 :
① 族个数 : 不需要事先确定 族个数 ;
② 形状 : 能发现 任意形状的族 ;
③ 异常值 : 对异常数据不敏感 ;
④ 聚类速度快 ;
DBSCAN 算法缺点 :
① 输入参数 ε \varepsilon ε 和 M i n P t s \rm MinPts MinPts 的值比较难确定 ;
② 数据库中 数据对象密度分布不均匀 时 , 使用相同的参数值可能无法得到好的聚类结果 ;
七、 支持度 置信度
给定 X , Y \rm X , Y X,Y 两个项集 , 并且有 X ≥ Y \rm X \geq Y X≥Y ;
支持度 : X ⇒ Y \rm X \Rightarrow Y X⇒Y 的支持度是 X , Y \rm X , Y X,Y 两个项集在数据库 D \rm D D 中 同时出现的概率 , 即 P r ( X ∪ Y ) \rm Pr(X \cup Y) Pr(X∪Y)
置信度 : X ⇒ Y \rm X \Rightarrow Y X⇒Y 的置信度度是 X \rm X X 出现的前提下 , Y \rm Y Y 项集在数据库 D \rm D D 中同时出现的概率 , 即 P r ( Y ∣ X ) = P r ( X ∪ Y ) P r ( X ) \rm Pr(Y|X) = \cfrac{Pr(X \cup Y)}{Pr(X)} Pr(Y∣X)=Pr(X)Pr(X∪Y)
一般情况下 置信度 大于 支持度 ;
八、 频繁项集
项集 X \rm X X 的 支持度 s u p p o r t ( X ) \rm support(X) support(X) , 大于等于 指定的 最小支持度阈值 m i n s u p \rm minsup minsup ,
则称该 项集 X \rm X X 为 频繁项集 ,
又称为 频繁项目集 ;
九、 非频繁项集
项集 X \rm X X 的 支持度 s u p p o r t ( X ) \rm support(X) support(X) , 小于 指定的 最小支持度阈值 m i n s u p \rm minsup minsup ,
则称该 项集 X \rm X X 为 非频繁项集 ,
又称为 非频繁项目集 ;
十、 Apriori 算法过程
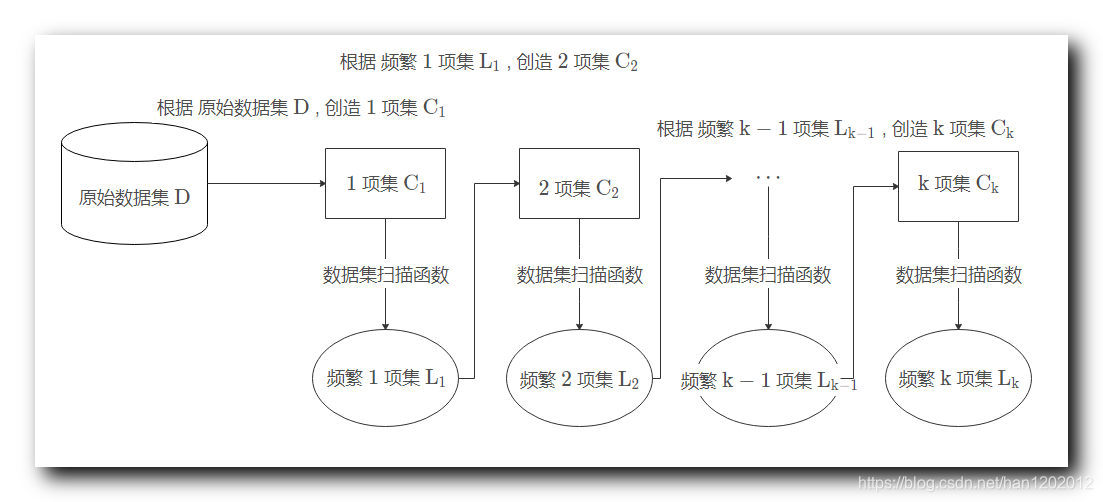
原始数据集 D \rm D D ,
1 1 1 项集 C 1 \rm C_1 C1 , 2 2 2 项集 C 2 \rm C_2 C2 , ⋯ \cdots ⋯ , k \rm k k 项集 C k \rm C_k Ck , 这些项集都是候选项集 ,
根据 原始数据集 D \rm D D , 创造 1 1 1 项集 C 1 \rm C_1 C1 , 然后对 C 1 \rm C_1 C1 执行 数据集扫描函数 , 找到其中的 频繁 1 1 1 项集 L 1 \rm L_1 L1 ,
根据 频繁 1 1 1 项集 L 1 \rm L_1 L1 , 创造 2 2 2 项集 C 2 \rm C_2 C2 , 然后对 C 2 \rm C_2 C2 执行 数据集扫描函数 , 找到其中的 频繁 2 2 2 项集 L 2 \rm L_2 L2 ,
⋮ \vdots ⋮
根据 频繁 k − 1 \rm k-1 k−1 项集 L k − 1 \rm L_{k-1} Lk−1 , 创造 k \rm k k 项集 C k \rm C_k Ck , 然后对 C k \rm C_k Ck 执行 数据集扫描函数 , 找到其中的 频繁 k \rm k k 项集 L k \rm L_k Lk ,
参考博客 : 【数据挖掘】关联规则挖掘 Apriori 算法 ( Apriori 算法过程 | Apriori 算法示例 )
文章来源: hanshuliang.blog.csdn.net,作者:韩曙亮,版权归原作者所有,如需转载,请联系作者。
原文链接:hanshuliang.blog.csdn.net/article/details/111872844
- 点赞
- 收藏
- 关注作者


评论(0)