在AI Studio上部署外部可以直接调用的云端服务
简 介: 按照 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆 的例子,对于在云端部署可以直接调用的服务进行了测试。但最后没有能够测试成功。后面还需要通过具体的例子来测试完整进行AI Studio云端服务的功能。
关键词: Paddle,云端服务
§01 部署应用
对于一个训练好的模型,直接部署在云端可以减少对于局部运算资源的需求。这在一些局域网络通讯条件良好的情况下是快速验证和系统搭建的方式。
在 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆 中按照说明初步测试了 Ai Studio 中的趣味体验馆的搭建过程,不过最终测试结果并没有完成通过。下面计划使用一个更加简单的模型进行搭建,熟悉网络部署的过程。
1.1 简单模型
这个简单模型是使用单层的BP网络来实现 2021年人工神经网络第三题:函数逼近

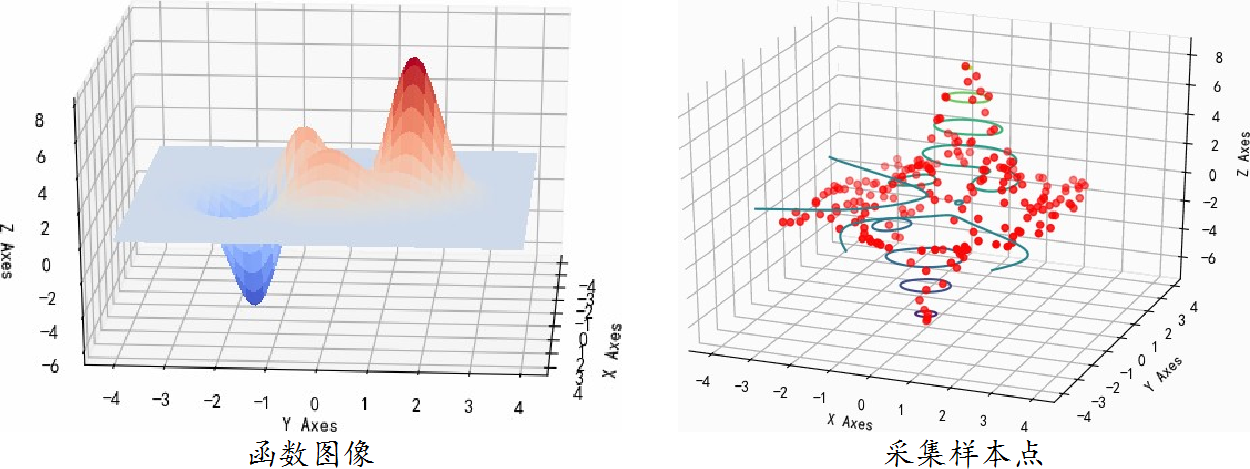
▲ 图1.1.1 二维函数的3D图像
1.1.1 样本
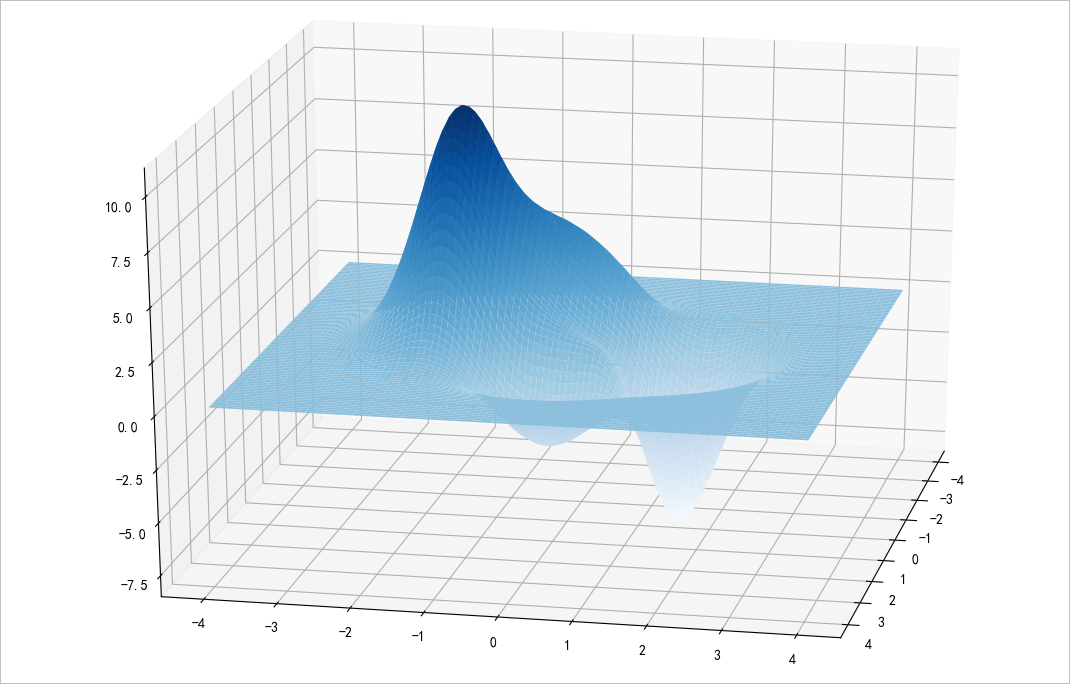
▲ 图1.1.2 二维函数图像模型
from headm import * # =
from mpl_toolkits.mplot3d import Axes3D
def fxy(x,y):
return 3*(1-x)**2*exp(-(x**2+(y+1)**2))+\
10*(x/5-x**3-y**5)*exp(-(x**2+y**2))-\
exp(-((x+1)**2+y**2))/3
grid_num = 100
x = linspace(-4,4,grid_num)
y = linspace(-4,4,grid_num)
x,y = meshgrid(x,y)
xx = x.flatten()
yy = y.flatten()
ff = fxy(xx,yy).reshape(x.shape)
ax = Axes3D(plt.figure(figsize=(12,8)))
ax.plot_surface(x,y,ff,
rstride=1,
cstride=1,
cmap=plt.cm.Blues)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
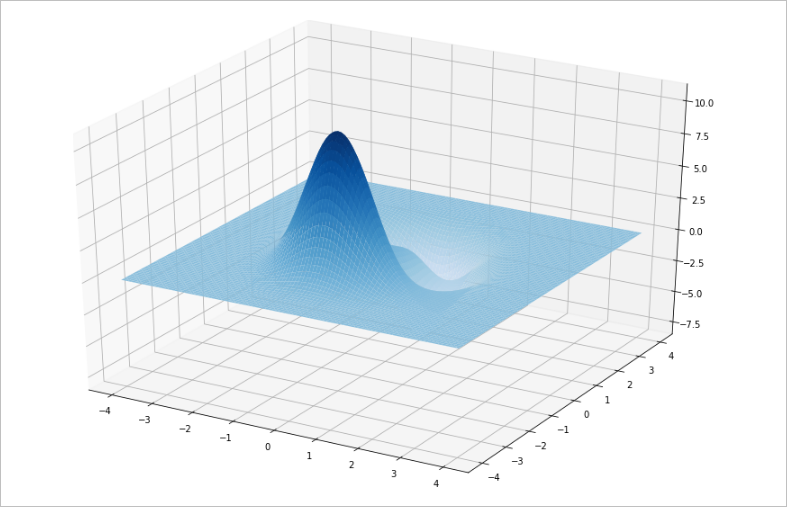
▲ 图1.1.3 二维函数图像模型
1.2 建立BP网络
1.2.1 建立数据加载对象
(1)数据加载代码
def fxy(x,y):
return 3*(1-x)**2*exp(-(x**2+(y+1)**2))+\
10*(x/5-x**3-y**5)*exp(-(x**2+y**2))-\
exp(-((x+1)**2+y**2))/3
grid_num = 100
x = linspace(-4,4,grid_num)
y = linspace(-4,4,grid_num)
x,y = meshgrid(x,y)
xx = x.flatten()
yy = y.flatten()
ff = fxy(xx,yy)
xy = array(list(zip(xx,yy)))
print(shape(ff), shape(xy))
class Dataset(paddle.io.Dataset):
def __init__(self, num_samples):
super(Dataset, self).__init__()
self.num_samples = num_samples
def __getitem__(self, index):
data = xy[index]
label = ff[index]
return paddle.to_tensor(data,dtype='float32'), paddle.to_tensor(label,dtype='float32')
def __len__(self):
return self.num_samples
_dataset = Dataset(len(ff))
train_loader = paddle.io.DataLoader(_dataset, batch_size=1000, shuffle=True)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
(2)测试数据加载代码
data = train_loader().next()
print("data: {}".format(data))
- 1
- 2
data: [Tensor(shape=[10, 2], dtype=float32, place=CPUPlace, stop_gradient=True,
[[ 0.52525252, -3.19191909],
[-1.57575762, 1.73737371],
[ 3.27272725, -1.73737371],
[ 4. , 2.78787875],
[ 2.14141417, -2.38383842],
[-3.35353541, 2.94949484],
[ 0.68686867, -0.52525252],
[ 1.73737371, -2.70707059],
[ 2.30303025, -2.14141417],
[ 3.83838391, -0.28282827]]), Tensor(shape=[10, 1], dtype=float32, place=CPUPlace, stop_gradient=True,
[[ 0.09874938],
[-0.50992441],
[-0.00000177],
[-0.00000011],
[ 0.02933590],
[-0.00000427],
[-0.56279999],
[ 0.04941760],
[ 0.02375283],
[-0.00019992]])]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
1.2.2 构建网络
class bpnn(paddle.nn.Layer):
def __init__(self, ):
super(bpnn, self).__init__()
self.L1 = paddle.nn.Linear(in_features=2, out_features=120)
self.L2 = paddle.nn.Linear(in_features=120, out_features=1)
def forward(self, x):
x = self.L1(x)
x = paddle.nn.functional.sigmoid(x)
x = self.L2(x)
return x
model = bpnn()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Linear-1 [[1000, 2]] [1000, 120] 360
Linear-2 [[1000, 120]] [1000, 1] 121
===========================================================================
Total params: 481
Trainable params: 481
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.01
Forward/backward pass size (MB): 0.92
Params size (MB): 0.00
Estimated Total Size (MB): 0.93
---------------------------------------------------------------------------
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
1.2.3 训练网络
optimizer = paddle.optimizer.Adam(learning_rate=0.1, parameters=model.parameters())
def train(model):
model.train()
epochs = 50
for epoch in range(epochs):
for batch, data in enumerate(train_loader()):
out = model(data[0])
loss = paddle.nn.functional.square_error_cost(out, data[1])
acc = fluid.layers.mean(loss)
loss.backward()
optimizer.step()
optimizer.clear_grad()
print('Epoch:{}, Accuracys:{}'.format(epoch, acc.numpy()))
train(model)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
paddle.summary(model, (1000,2))
paddle.save(model.state_dict(), './work/model.pdparams')
- 1
- 2
1.2.4 验证网络
(1)读取网络参数
class bpnn(paddle.nn.Layer):
def __init__(self, ):
super(bpnn, self).__init__()
self.L1 = paddle.nn.Linear(in_features=2, out_features=120)
self.L2 = paddle.nn.Linear(in_features=120, out_features=1)
def forward(self, x):
x = self.L1(x)
x = paddle.nn.functional.sigmoid(x)
x = self.L2(x)
return xa
model = bpnn()
model.set_state_dict(paddle.load('./work/model.pdparams'))
out = model(paddle.to_tensor(xy, dtype=float32)).numpy()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
(2)计算网络预测误差
outdif = out.flatten() - ff
print(shape(outdif), shape(out), shape(ff))
errff = outdif.reshape(x.shape)
ax = Axes3D(plt.figure(figsize=(12,8)))
ax.plot_surface(x,y,errff,
rstride=1,
cstride=1,
cmap=plt.cm.Blues)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
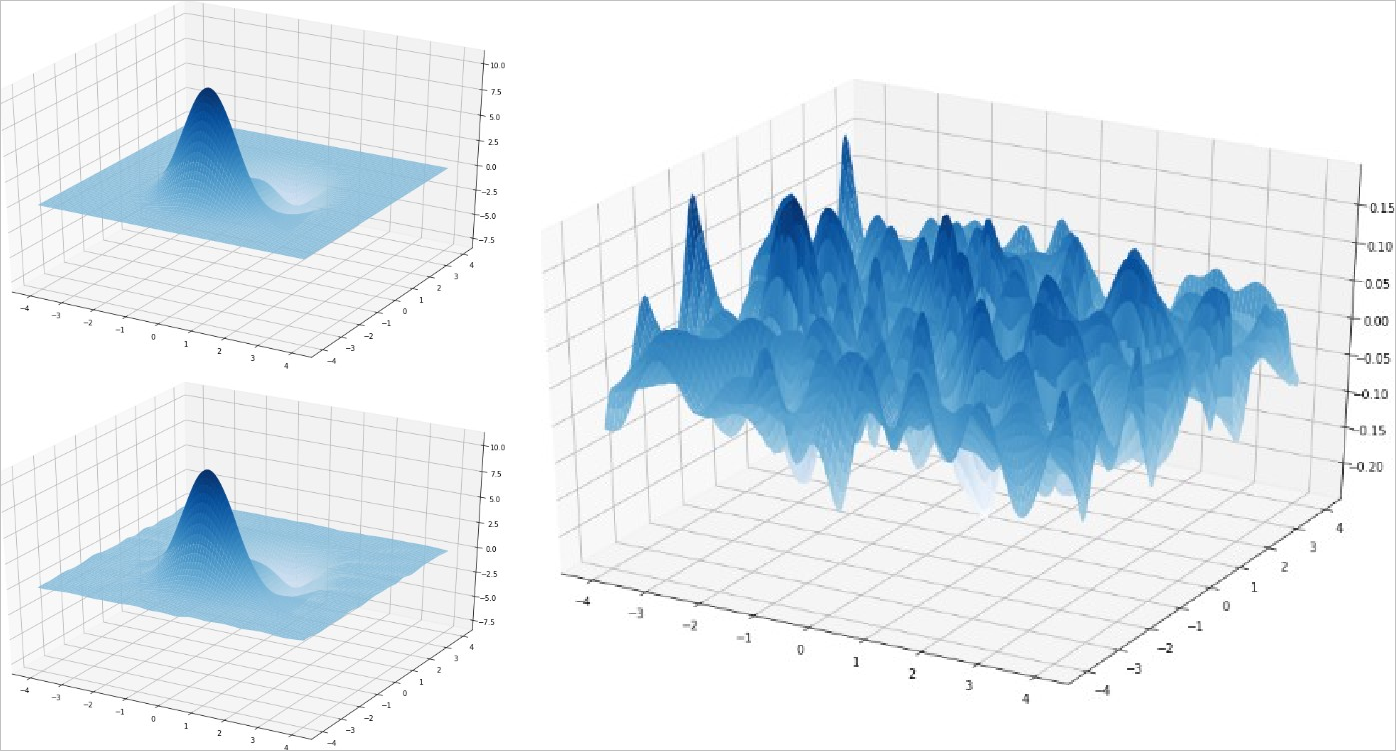
▲ 图1.2.1 原始数据,恢复数据以及数据误差
1.3 部署应用
参考Paddle相关的资料: 模型保存与载入
根据 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆 介绍的 模型部署流程 中的内容,需要将模型转换成静态模型。
1.3.1 转换模型
在 PaddlePaddle文档:动态图转静态图 给出了动态图转换成静态图的方法。
(1)什么是动态图和静态图
在深度学习模型构建上,飞桨框架支持动态图编程和静态图编程两种方式,其代码编写和执行方式均存在差异。
-
动态图编程: 采用 Python 的编程风格,解析式地执行每一行网络代码,并同时返回计算结果。在 模型开发 章节中,介绍的都是动态图编程方式。
-
静态图编程: 采用先编译后执行的方式。需先在代码中预定义完整的神经网络结构,飞桨框架会将神经网络描述为 Program 的数据结构,并对 Program 进行编译优化,再调用执行器获得计算结果。
动态图编程体验更佳、更易调试,但是因为采用 Python 实时执行的方式,开销较大,在性能方面与 C++ 有一定差距;静态图调试难度大,但是将前端 Python 编写的神经网络预定义为 Program描述,转到 C++ 端重新解析执行,脱离了 Python 依赖,往往执行性能更佳,并且预先拥有完整网络结构也更利于全局优化。
(2)什么情况下将动态图转换成静态图?
飞桨框架在设计时,考虑同时兼顾动态图的高易用性和静态图的高性能优势,采用『动静统一』的方案:
-
在模型开发时,推荐采用动态图编程。 可获得更好的编程体验、更易用的接口、更友好的调试交互机制。
-
在模型训练或者推理部署时,只需添加一行装饰器 @to_static,即可将动态图代码转写为静态图代码,并在底层自动使用静态图执行器运行。 可获得更好的模型运行性能。
方案如下图所示:
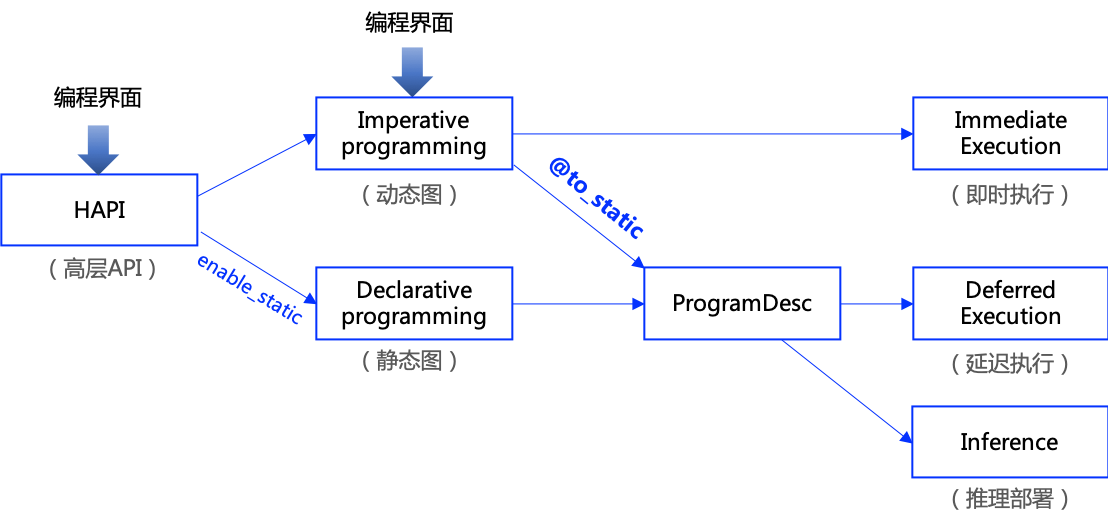
▲ 图1.3.1 飞桨框架动静统一方案
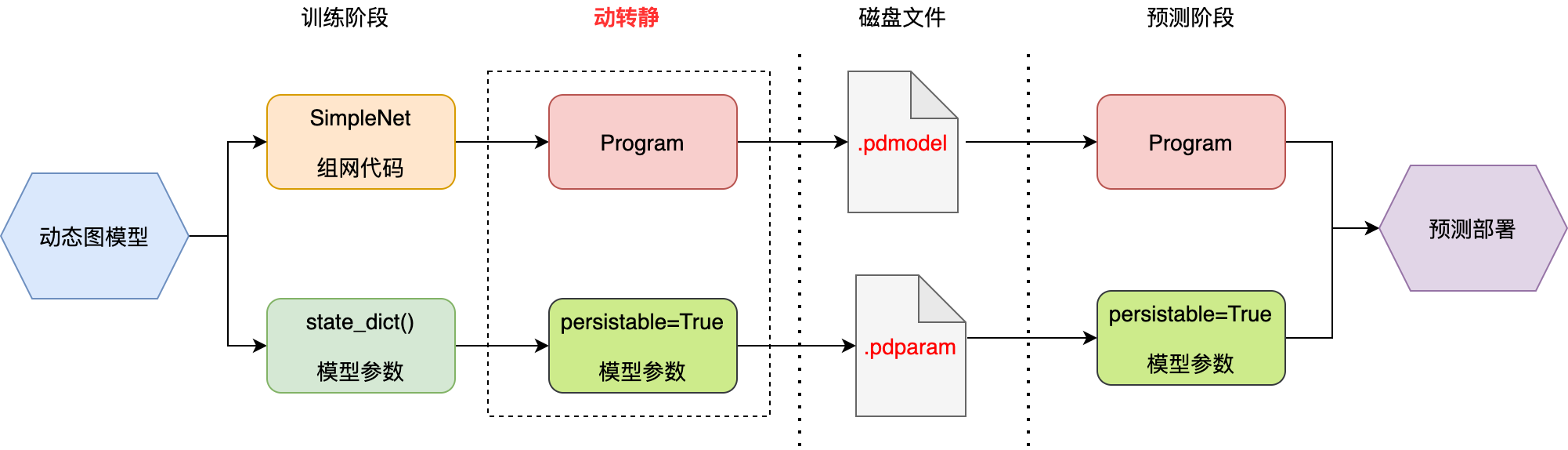
▲ 图1.3.2 动静转换模式
(3)转换举例
Ⅰ.利用@to_static装饰forward函数
import paddle
from paddle.jit import to_static
class SimpleNet(paddle.nn.Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
@to_static # 动静转换
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
net = SimpleNet()
net.eval()
x = paddle.rand([2, 10])
y = paddle.rand([2, 3])
out = net(x, y)
paddle.jit.save(net, './net')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Ⅱ.
import paddle
from paddle.jit import to_static
class SimpleNet(paddle.nn.Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
net = SimpleNet()
net.eval()
net = paddle.jit.to_static(net) # 动静转换
x = paddle.rand([2, 10])
y = paddle.rand([2, 3])
out = net(x, y)
paddle.jit.save(net, './net')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
注意, 在paddle.jit.save() 直接需要通过 net.eval(),以及后面的out=net(x,y)能够进行input_spec。否则就会出错。
(4)将bpnn转换成静态图
import paddle
from paddle.jit import to_static
class bpnn(paddle.nn.Layer):
def __init__(self, ):
super(bpnn, self).__init__()
self.L1 = paddle.nn.Linear(in_features=2, out_features=120)
self.L2 = paddle.nn.Linear(in_features=120, out_features=1)
def forward(self, x):
x = self.L1(x)
x = paddle.nn.functional.sigmoid(x)
x = self.L2(x)
return x
model = bpnn()
model.set_state_dict(paddle.load('./work/model.pdparams'))
model = paddle.jit.to_static(model)
out = model(paddle.rand([2,2]))
print("out: {}".format(out))
paddle.jit.save(model, '/home/aistudio/work/net')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
1.3.2 部署过程
在具体按照 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆 不说AI Studio体验馆的过程中,发现仍然出现了测试错误。
※ 总 结 ※
按照 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆 的例子,对于在云端部署可以直接调用的服务进行了测试。但最后没有能够测试成功。后面还需要通过具体的例子来测试完整进行AI Studio云端服务的功能。
■ 相关文献链接:
- 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆
- 2021年人工神经网络第一次作业要求
- 模型保存与载入
- 百度上的快速部署的两个平台:EasyDL以及AI Studio体验馆
- PaddlePaddle文档:动态图转静态图
● 相关图表链接:
- 图1.1.1 二维函数的3D图像
- 图1.1.2 二维函数图像模型
- 图1.1.3 二维函数图像模型
- 图1.2.1 原始数据,恢复数据以及数据误差
- 图1.3.1 飞桨框架动静统一方案
- 图1.3.2 动静转换模式
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/122364402
- 点赞
- 收藏
- 关注作者


评论(0)