矩阵英文：Matrix是线性代数中最基础的内容

矩阵

由mn个数按一定的次序排成的m行n列的矩形数表成为mn的矩阵，简称矩阵。
（元素为实数的称为实矩）

行矩阵

在线性代数中，行向量或行矩阵是1×m阶矩阵，即由单行m个元素组成的矩阵，记作A=（a1 a2…am)，为避免元素间的混淆，也记作A=(a1，a2，…an)。

[ 1 2 3 ]

列矩阵

在线性代数中，列向量是一个 n×1 的矩阵，即矩阵由一个含有n个元素的列所组成：列向量的转置是一个行向量，反之亦然。所有的列向量的集合形成一个向量空间，它是所有行向量集合的对偶空间。

[ 1 2 3 ]

零矩阵

所有的元素都是0
[ 0 0 0 0 0 0 0 0 0 ]

对角阵

一定是方阵，对角线下标两个数相同

单位矩阵

主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵

[ 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 ] \left[

数量矩阵

主对角线都是k

[ k 2 ⋯ 4 7 k ⋯ 5 ⋮ ⋮ ⋱ ⋮ 8 9 ⋯ k ] \left[

梯形矩阵

若矩阵A满足两条件：（1）若有零行（元素全为0的行），则零行应在最下方；（2）非零首元（即非零行的第一个不为零的元素）的列标号随行标号的增加而严格递增，则称此矩阵A为阶梯形矩阵。

方阵

当m=n时，即矩阵的行数与列数相同时，称矩阵为方阵。
方阵有主对角线，不是方阵没有主对角线

例：

1 2 3 4 5 6 7 8 9

矩阵加法减法

被定义在两个相同大小的矩阵
简言之，两个矩阵相加减，即它们相同位置的元素相加减！
A+(B+C) = (A+B)+C

矩阵乘法

1.矩阵与数的乘法

　结合律： (λμ)A=λ(μA)      (λ+μ)A =λA+μA
　分配律： λ (A+B)=λA+λB

  

 

  
1
  
2
 

2.矩阵与矩阵的乘法

设A= $(a_{ij}{)}_{m\times s}$，B=$(a_{ij}{)}_{s\times n}$ 则A与B的乘积是这样一个矩阵：
　　(1) 行数与（左矩阵）A相同，列数与（右矩阵）B相同，即．
　　(2) C的第行第列的元素由A的第行元素与B的第列元素对应相乘，再取乘积之和．
　　
乘法结合律： (AB)C=A(BC)． [3]
乘法左分配律：(A+B)C=AC+BC [3]
乘法右分配律：C(A+B)=CA+CB [3]

例：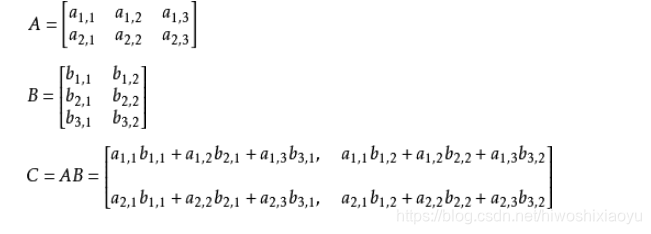

文章来源: yujiang.blog.csdn.net，作者：鱼酱2333，版权归原作者所有，如需转载，请联系作者。

原文链接：yujiang.blog.csdn.net/article/details/102494024