🎈 作者：Linux猿

🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！

🎈 关注专栏： 动图讲解数据结构和算法 （优质好文持续更新中……）🚀

🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

目录

一、什么是相互转换

二、树与二叉树的相互转换

2.1 树转换为二叉树

2.2 树转换二叉树实例

2.2 二叉树转换为树

2.3 二叉树转换为树实例

三、森林与二叉树的相互转换

3.1 森林转换为二叉树

3.2 森林转换为二叉树实例

3.3 二叉树转换为森林

3.4 二叉树转换为森林实例

四、总结

 在对树进行一些操作时，比如：遍历树，存储树等，并没有非常方便的数据结构来存储，那么，可以将树转换为二叉树，可以使用二叉链表来存储，这样就方便多了。接下来，本篇文章来讲解下二叉树、树和森林的相互转换，赶紧来看一下吧！

一、什么是相互转换

正如文章开头所提到的，不规则的树并没有非常合适的数据结构来存储，而二叉树有多中存储方式，比如：双亲表示法，孩子表示法等。另一方面，给定一棵树，有唯一的一棵二叉树与之对应。这样就可以在树和二叉树之间作相互转换。

接下来将会介绍树与二叉树、森林与二叉树的相互转换。

二、树与二叉树的相互转换

2.1 树转换为二叉树

树转换为二叉树的步骤如下所示：

步骤一：兄弟连线，在树的相邻兄弟结点之间连线；

步骤二：删原连线，删除原父结点与孩子结点的连线，仅保留每个父结点与第一个孩子结点的连线；

步骤三：层次调整，调整树的层次结构，使其成为一棵二叉树。

下面来看一个例子来加深理解。

2.2 树转换二叉树实例

假设有如下一棵树，如下图所示。

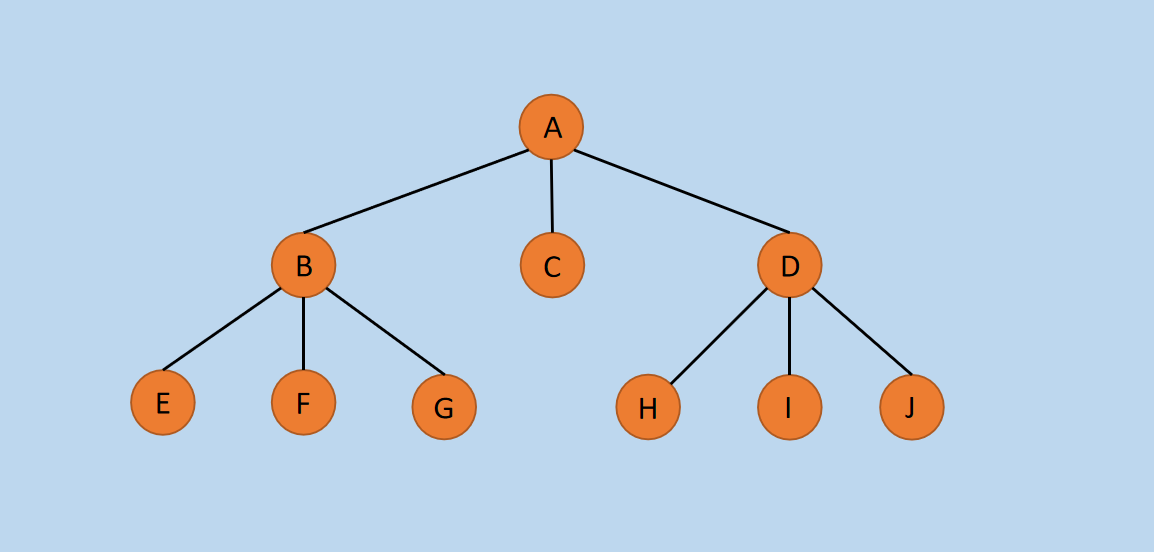图1  树

（1）在树的相邻兄弟结点之间连线，连线后如下图所示。 

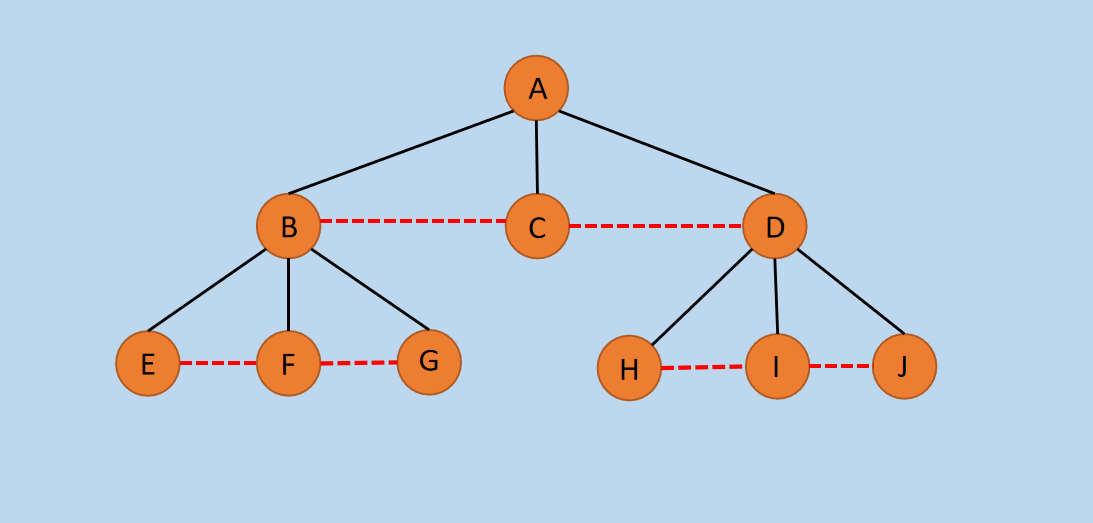图2 兄弟连线后

 在上图中，树中的相邻兄弟结点连接了红色虚线，包括：BC、CD、EF、FG等的连线，注意：是相邻的兄弟结点连线。

 （2）删除原树父结点与子节点的连线，注意：保留每个父结点与第一个孩子结点的连线，如下所示。

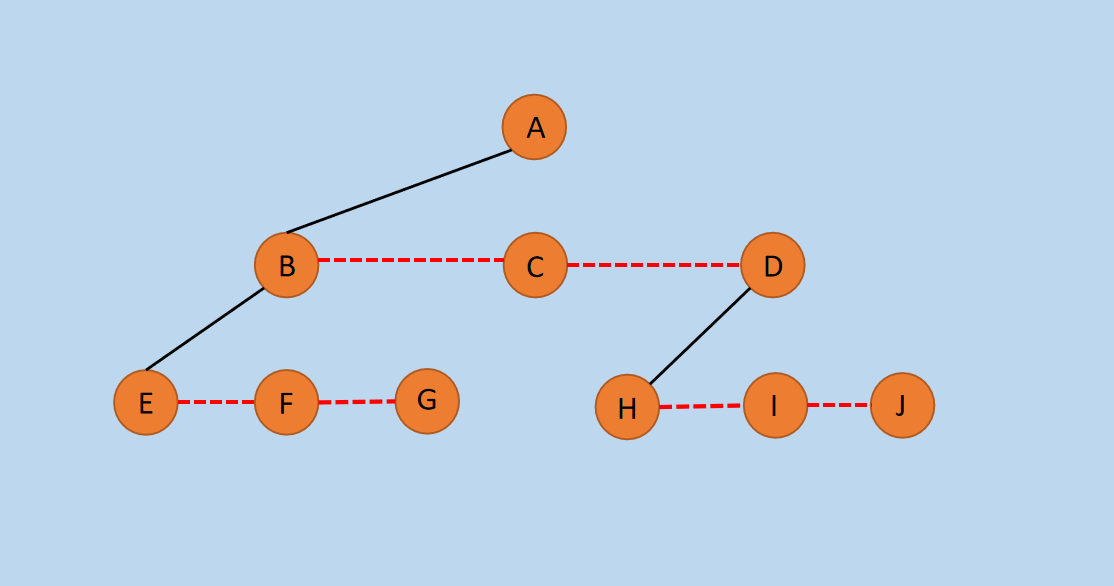图3 删除父结点与子节点的连线

 如上图所示，删除了 AC、AD、BF、BG、DI、DJ的连线，这时候已经是一棵二叉树了，下面来调整下二叉树的层次结构。

（3）以根结点 A 为基础，调整结点的层次结构，如下所示。

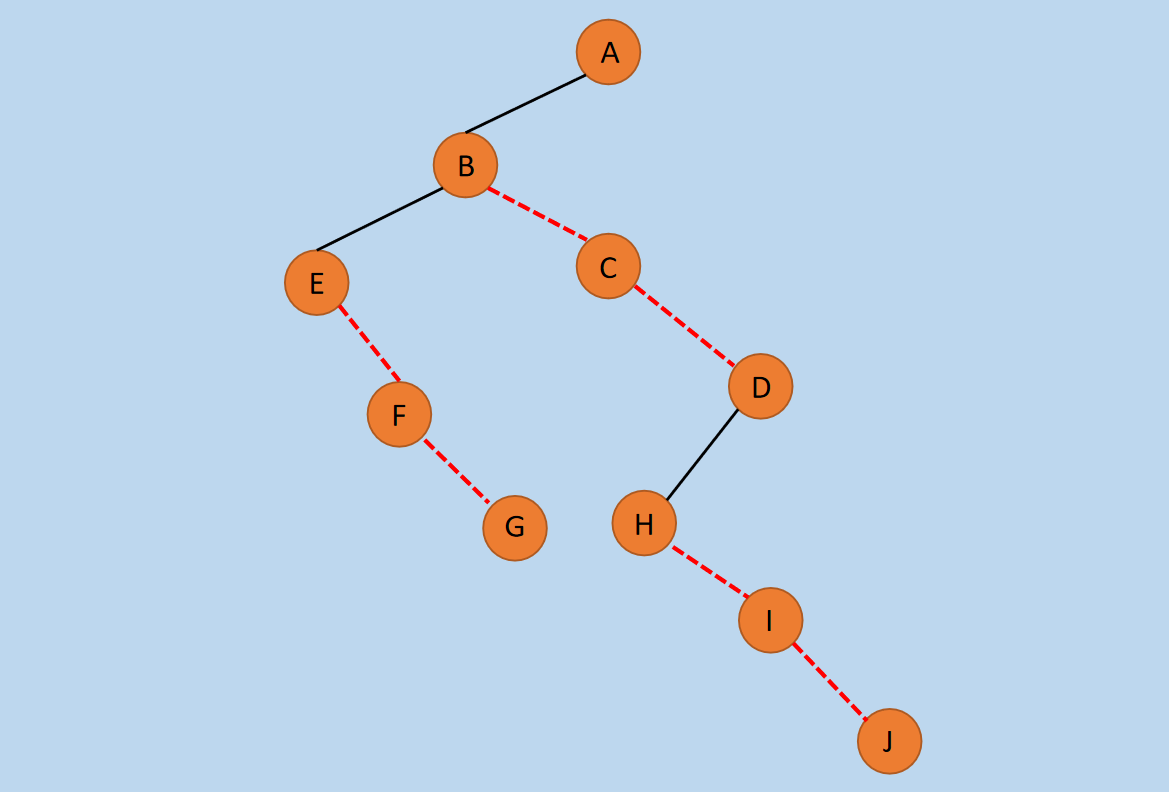图4 调整后的二叉树

如上图所示，经过调整后成为了一棵正规的二叉树。

2.2 二叉树转换为树

二叉树转换为树的步骤如下所示：

步骤一：连线右孩子，如果结点 i 的左孩子存在，则将结点 i 与左孩子的右孩子结点、左孩子的右孩子的右孩子结点，…… 连线。

步骤二：删原连线，删除原二叉树中所有父结点与其右孩子结点的连线。

步骤三：层次调整，调整转换后的二叉树的层次结构。

2.3 二叉树转换为树实例

假设有如下二叉树，如下图所示。

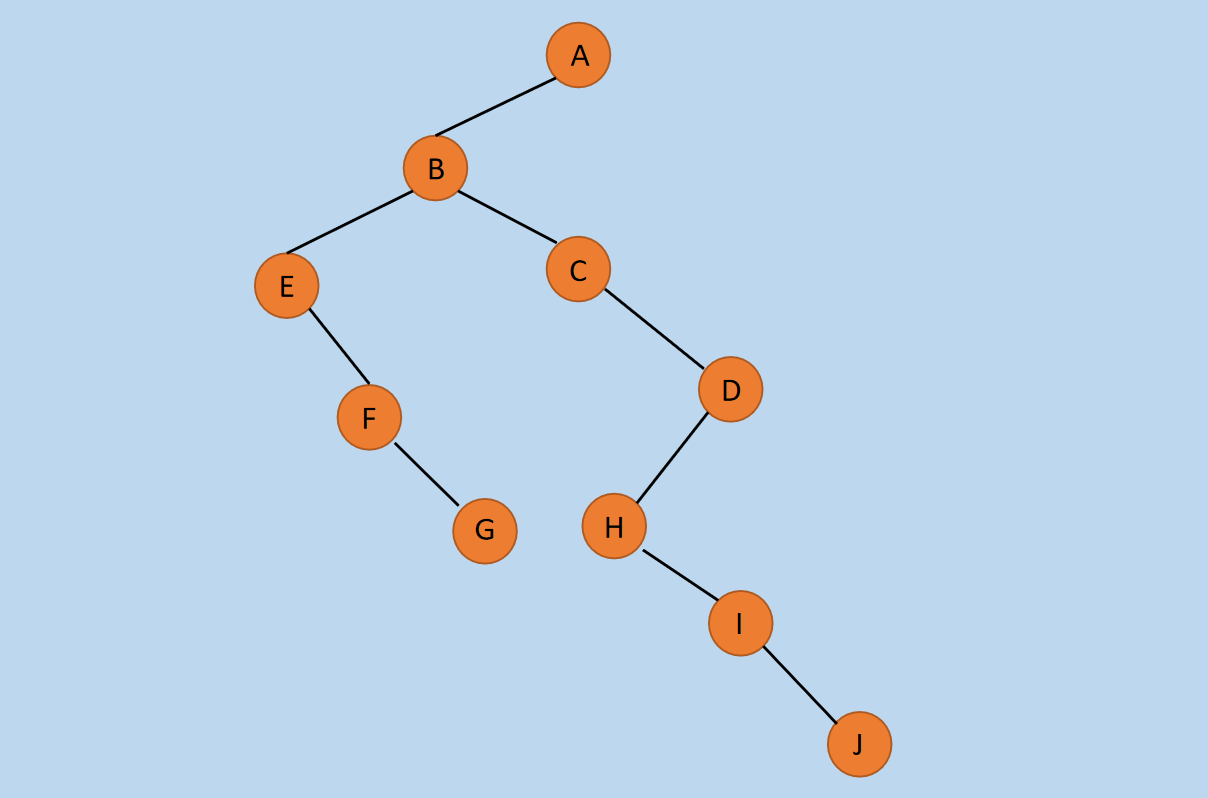图4 二叉树

 （1）将每个父节点与左孩子的右孩子结点，左孩子的右孩子的右孩子结点，……连线，注意：是每一个父结点，如下所示。

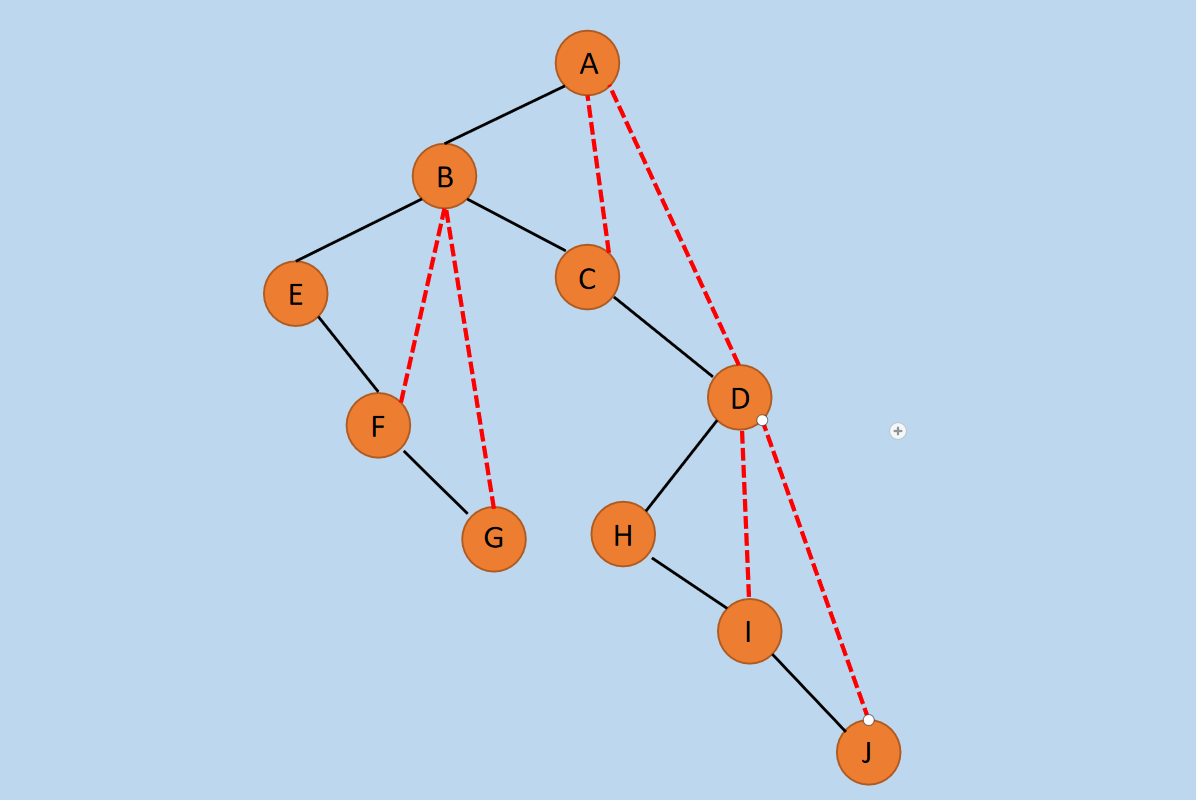图6 连线

在上图中，结点 A 与左孩子 B 的右节点 C，左孩子 B 的右孩子 C 的右孩子 D 进行了连线，其它父结点同理，如上图的 红色 虚线所示。

（2）删除原二叉树中每个父节点与右孩子的连线，如下所示。

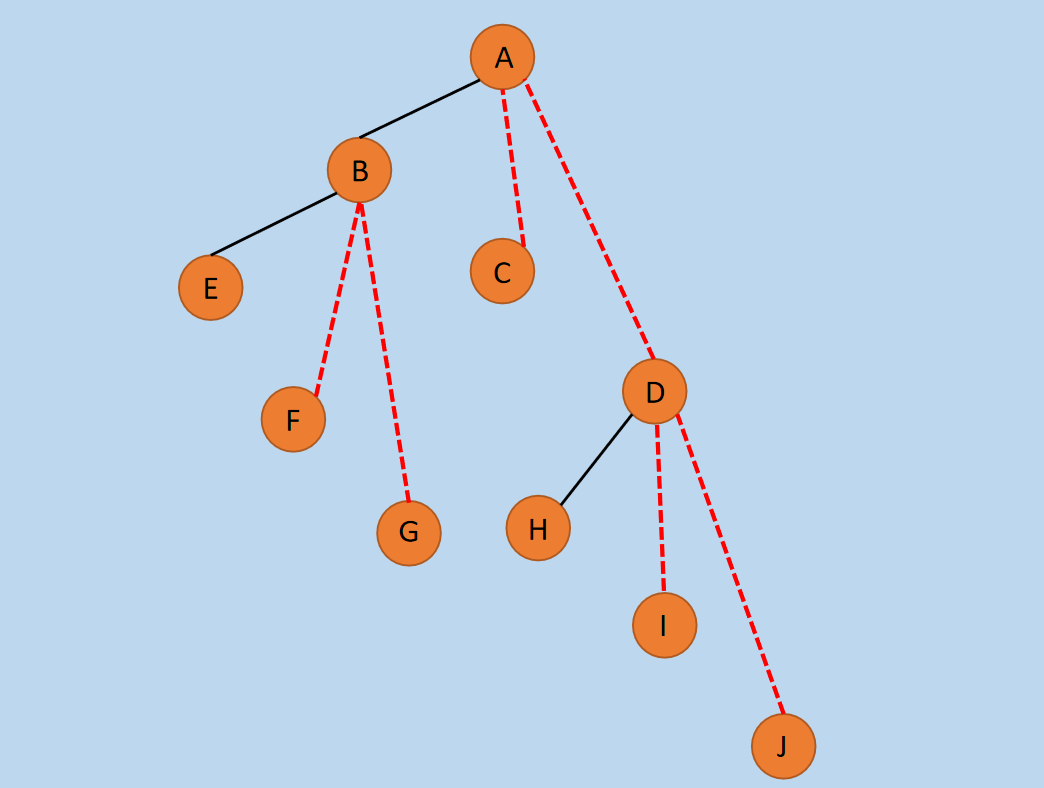图7 删除连线

在上图中，分别删除了 BC、CD、EF、FG 等的连线。

（3）层次调整，将当前的树进行调整，将同一个层次的结点调整到相同层，如下所示。

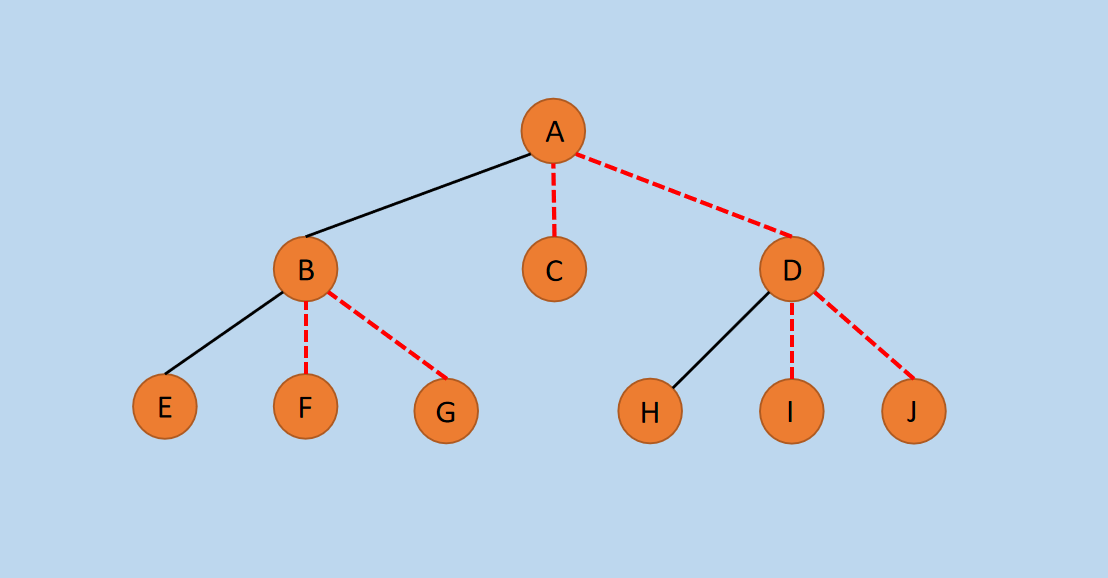图8 调整层次

经过调整后成为了一棵树，这棵树和 2.2 中的树是一致的。

三、森林与二叉树的相互转换

3.1 森林转换为二叉树

森林转换为二叉树的步骤如下所示：

步骤一：先将森林中的每一棵树转换为二叉树，参见 2.1 树转换为二叉树；

步骤二：第一颗二叉树不变，其它的二叉树依次作为前一个二叉树的右子树；

下面来看一个例子加深理解。

3.2 森林转换为二叉树实例

假设有如下森林，如下图所示。

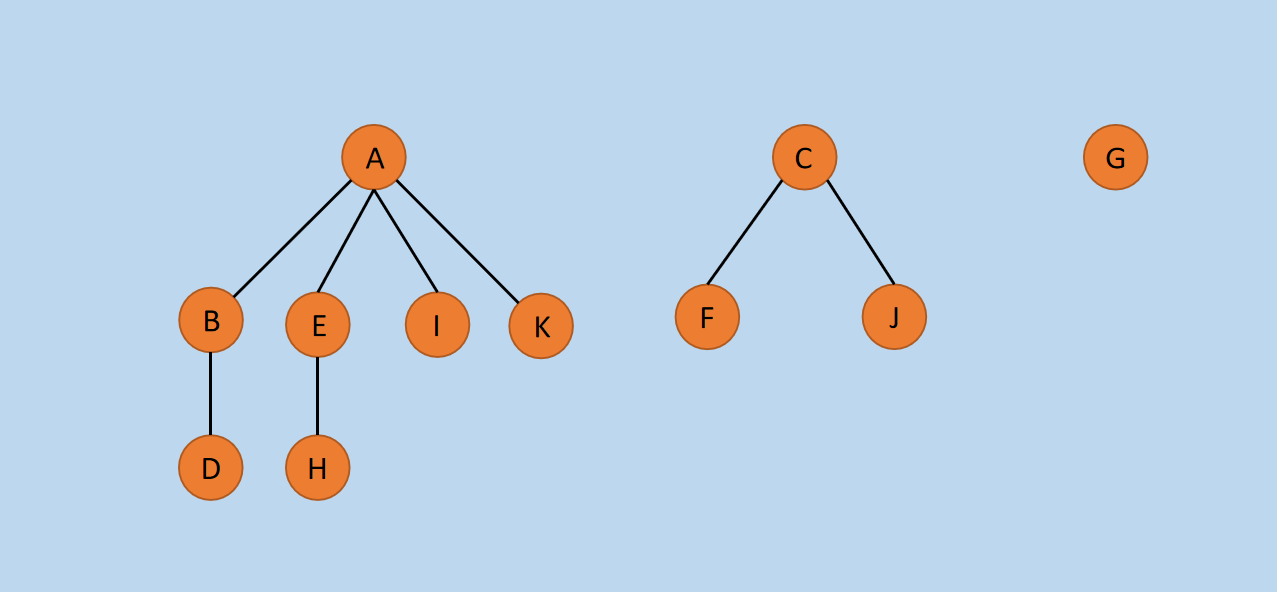图9 森林

（1）首先，将森林中的每一颗树转换为二叉树，转换后如下图所示。

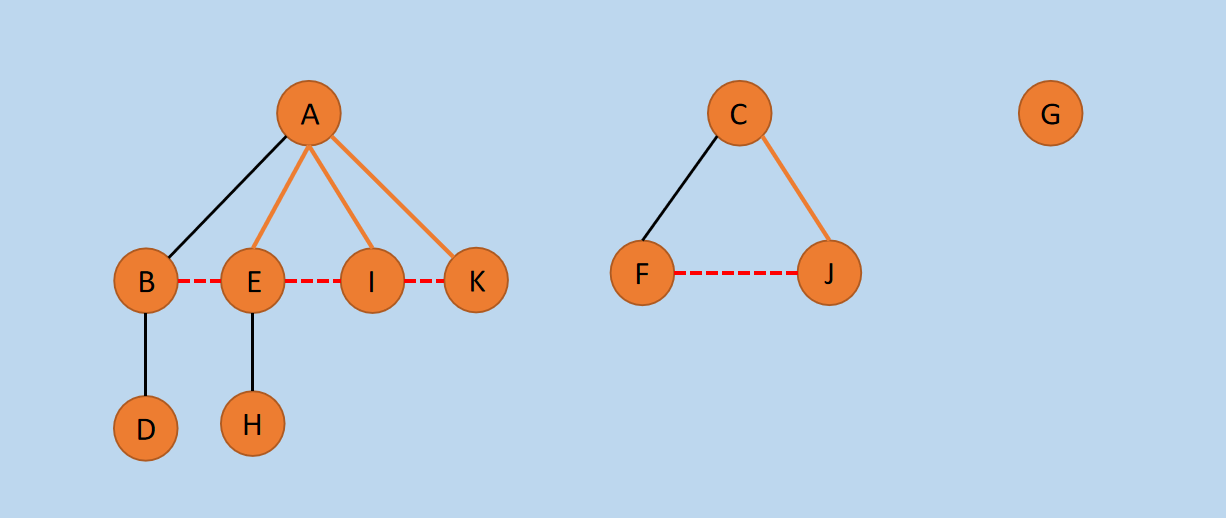图10 树转换为二叉树

先将森林中的每一颗树转换为二叉树，转换过程同树转换为二叉树，转换后如下所示。

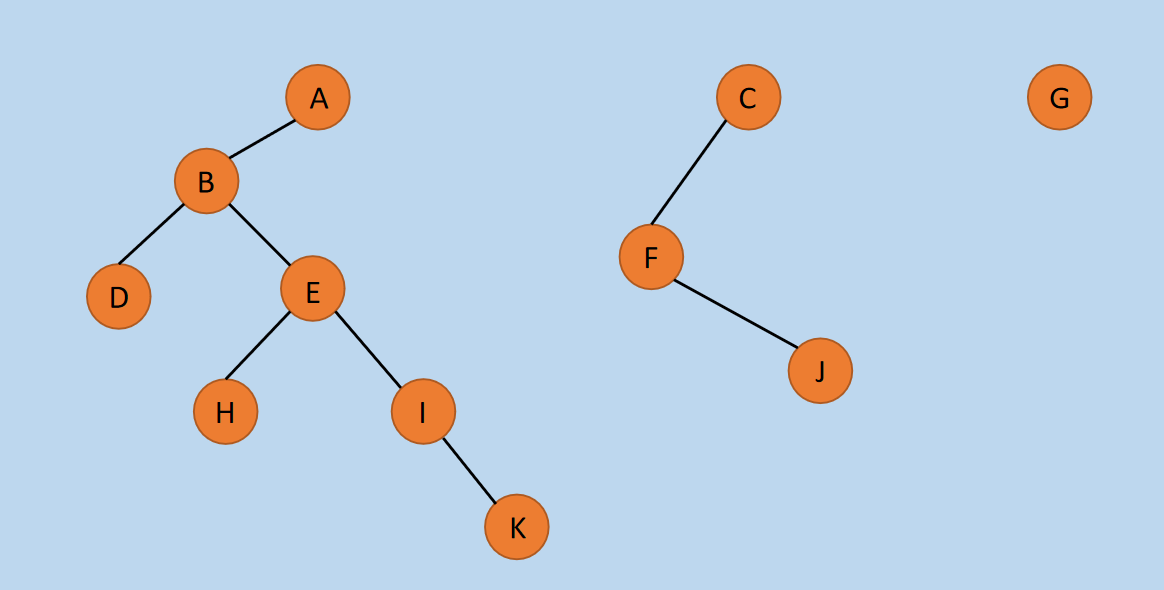图11 树转换为二叉树后

（2）将转换后的所有二叉树组成一个二叉树，组合后如下图所示。

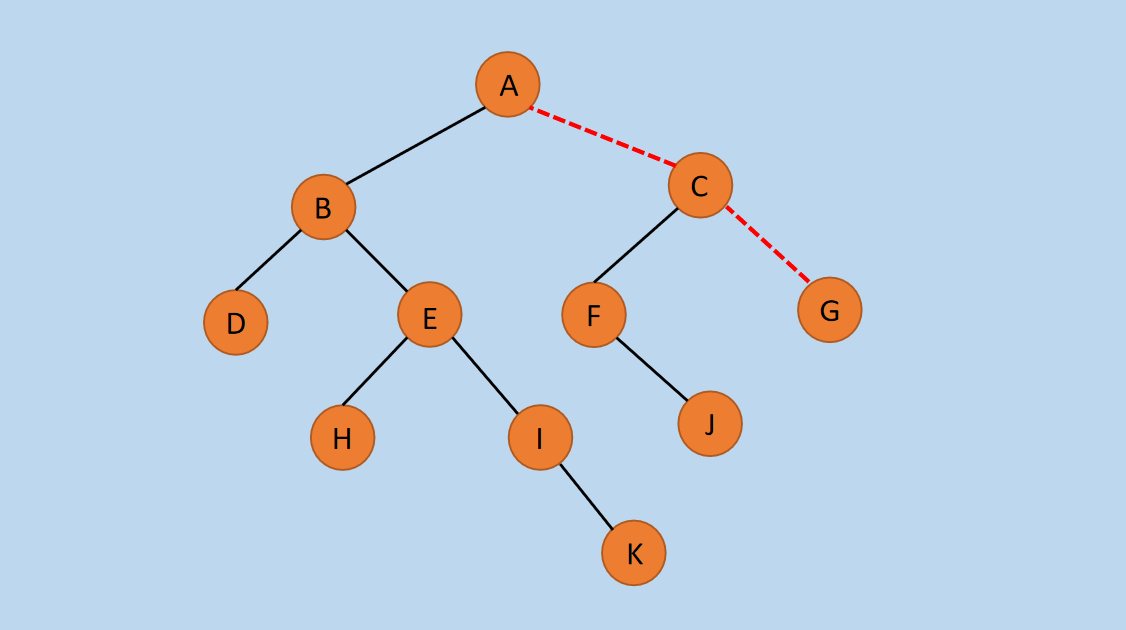图12 转换后的二叉树

在上图中，红色虚线表示添加的连接，除了第一颗子树外，其它子树都成为了前一棵子树的右子树。

3.3 二叉树转换为森林

二叉树转换为森林的步骤如下所示：

步骤一：将二叉树根结点与它的右子树、根结点的右子树与右子树……的连线去掉；

步骤二：将拆分后的每一个二叉树转换为树。

下面来看一个例子加深理解。

3.4 二叉树转换为森林实例

假设有如下二叉树，如下图所示。

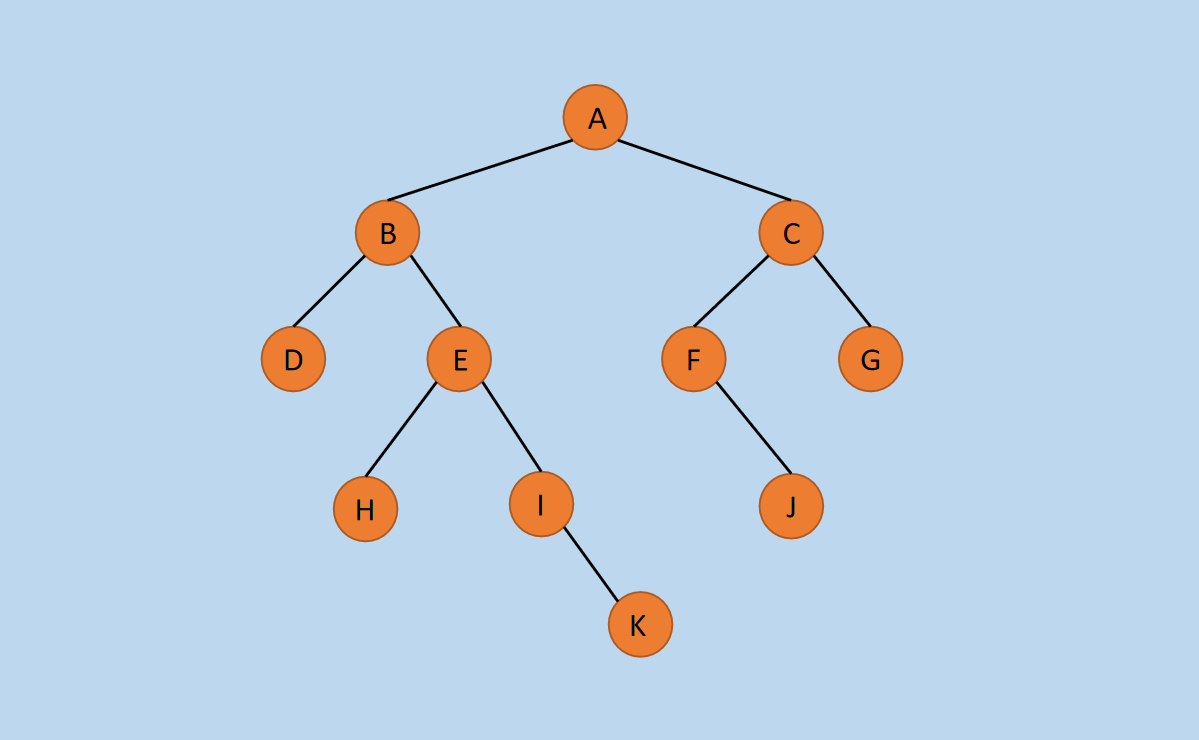图13 二叉树

 （1）首先，将二叉树拆分开，拆分后如下所示。

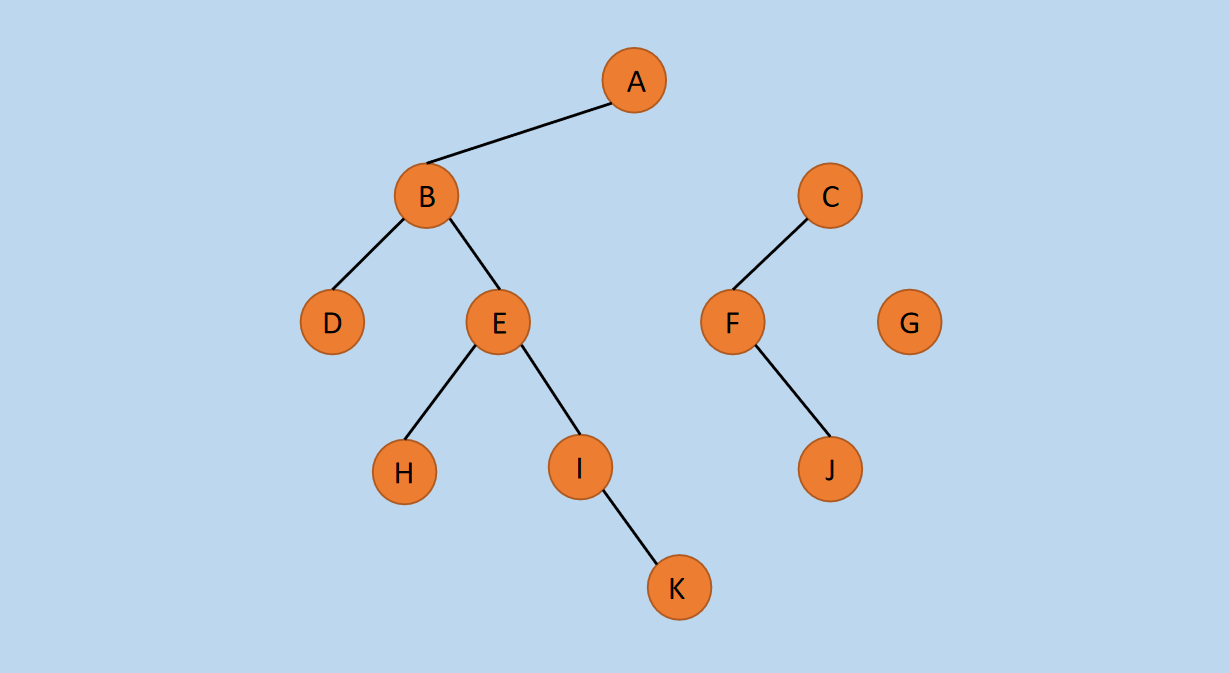图14 森林

（2）然后，将拆分后的每一个二叉树转换为树，如下所示。

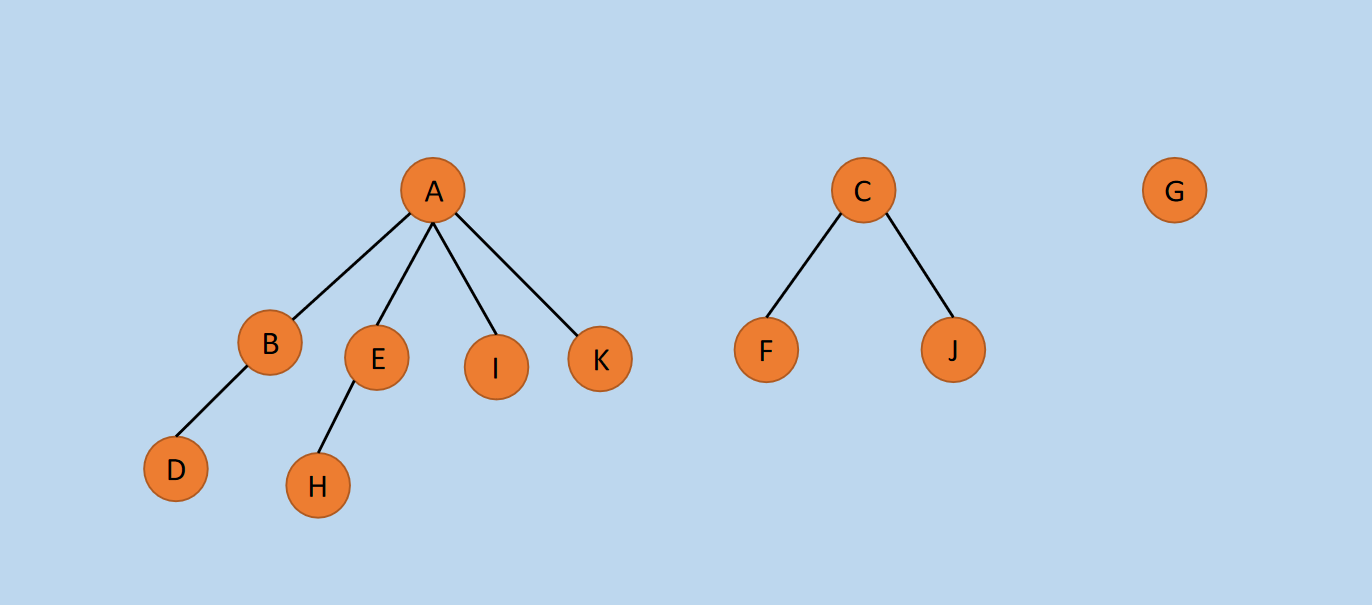图15 转换后的森林

四、总结

本文主要对二叉树与树和森林之间的相互转换进行了详细的讲解，需要掌握转换的方法。

🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓

【博客之星活动】希望路过的小伙伴支持下猿哥 点击链接，拉到文章结尾，点击五星！感谢支持！🌹🌹🌹🌹🌹🌹🌹🌹

电脑端的小伙伴可以点击这里：主页左上角

猿哥将一如既往的更新优质文章回馈大家！

🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓🍓

文章来源: blog.csdn.net，作者：Linux猿，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nyist_zxp/article/details/122144638