树的遍历

树的遍历（也称为树的搜索），树的遍历指的是按照某种规则，不重复地访问某种树的所有节点的过程。树的遍历不同于链表，队列，栈这些线性数据结构，树结构有多种不同的遍历方式，可以分为：

• 深度优先遍历 ：前序遍历/中序遍历/后序遍历
• 广度优先遍历
  二者的区别在于
  深度优先搜索先访问子节点，再访问父节点，最后是第二个子节点；
  广度优先搜索先访问第一个子节点，再访问第二个子节点，最后访问父节点；

深度优先遍历

下面，对下图所示的二叉树进行深度优先遍历，同样，结果不唯一，将按照前序/中序/后序分别加以区分；

前序遍历（Pre Order Traversal）

前序遍历指的是先访问根，然后再访问子树的遍历方式；

F, B, A, D, C, E, G, I, H.

中序遍历（In Order Traversal）

• 先访问左子树，然后访问根，再访问右子树；

或者

• 先访问右子树，然后访问根，再访问左子树；

不过，一般按照第一种的方式进行中序遍历；

A, B, C, D, E, F, G, H, I.

后序遍历（Post Order Traversal）

先访问子树，再访问根的遍历方式；

A, C, E, D, B, H, I, G, F.

广度有限遍历

层序遍历（Level Order Traversal）

下图的遍历结果 F, B, G, A, D, I, C, E, H.

C++四种遍历实现

根据下图所示的二叉树，分别进行四种遍历的C++程序的实现，可以预先根据上面遍历的规则，计算四种遍历的结果，对比一下程序；

#include <iostream>
#include <vector>
#include <queue>
#define SIZE 50
using namespace std;

class TreeNode {
public:
	TreeNode(int x) : vali(x),valc(0),lchild(nullptr), rchild(nullptr) {}
	TreeNode(char x) : vali(0), valc(x), lchild(nullptr), rchild(nullptr) {}
	TreeNode(const TreeNode& treenode) {
		vali = treenode.vali;
		valc = treenode.valc;
	}
	char valc;
	int vali;
	TreeNode *lchild;
	TreeNode *rchild;

	static void post_order_traversal(TreeNode *root) {
		if (root->lchild != NULL)
			post_order_traversal(root->lchild);
		if (root->rchild != NULL)
			post_order_traversal(root->rchild);
		// Do Something with root
		cout << root->valc << " ";
	}
	static void in_order_traversal(TreeNode *root) {
		if (root->lchild != NULL)
			in_order_traversal(root->lchild);
		// Do Something with root
		cout << root->valc << " ";
		if (root->rchild != NULL)
			in_order_traversal(root->rchild);
	}

	static void pre_order_traversal(TreeNode *root) {
		// Do Something with root
		cout << root->valc << " ";
		if (root->lchild != NULL)
			pre_order_traversal(root->lchild);
		if (root->rchild != NULL)
			pre_order_traversal(root->rchild);
	}
	static void layer_traver(TreeNode *root) {
		int head = 0, tail = 0;
		TreeNode *p[SIZE] = { nullptr };
		TreeNode *tmp;
		if (root != nullptr) {
			p[head] = root;
			tail++;
			// Do Something with p[head]			
		} else {
			return;
		}
		//环形队列作为缓冲器
		while (head % SIZE != tail % SIZE) {			
			tmp = p[head % SIZE];
			// Do Something with p[head]			
			cout << tmp->valc << " ";
			if (tmp->lchild != NULL) { // left
				p[tail++ % SIZE] = tmp->lchild;				
			}
			if (tmp->rchild != NULL) { // right
				p[tail++ % SIZE] = tmp->rchild;				
			}
			head++;
		}
		return;
	}	
	
	static void layer_traver_stl(TreeNode *root) {
		queue<TreeNode*> node_list;
		TreeNode *tmp;
		if (root != nullptr) {
			node_list.push(root);
			// Do Something with p[head]			
		}
		else {
			return;
		}
		while (node_list.size()) {		
			tmp = node_list.front();
			node_list.pop();
			cout << tmp->valc << " ";
			if (tmp->lchild != NULL) { // left
				node_list.push(tmp->lchild);
			}
			if (tmp->rchild != NULL) { // right
				node_list.push(tmp->rchild);
			}
		}
		return;
	}
};

int main() {
	TreeNode root('A');

	TreeNode node1('B');
	TreeNode node2('C');
	TreeNode node3('D');
	TreeNode node4('E');
	TreeNode node5('F');
	TreeNode node6('G');
	TreeNode node7('H');
	TreeNode node8('I');
	TreeNode node9('J');
	TreeNode node10('K');
	
	root.lchild = &node1;
	node1.lchild = &node3;
	node1.rchild = &node4;
	node3.lchild = &node7;
	node3.rchild = &node8;
	node4.lchild = &node9;
	root.rchild = &node2;
	node2.lchild = &node5;
	node2.rchild = &node6;
	node6.lchild = &node10;

	cout << "\n前序遍历：";
	TreeNode::pre_order_traversal(&root);
	cout << "\n中序遍历：";
	TreeNode::in_order_traversal(&root);
	cout << "\n后序遍历：";
	TreeNode::post_order_traversal(&root);
	cout << "\n层序遍历01：";
	TreeNode::layer_traver(&root);
	cout << "\n层序遍历02：";
	TreeNode::layer_traver_stl(&root);
	getchar();
	return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
 

程序最终运行结果如下：

二叉树遍历的其他例子

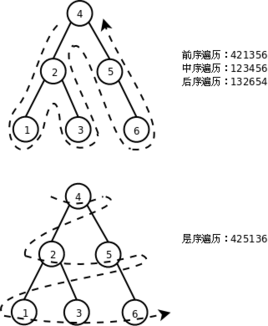
下面额外在网络上收集了多个二叉树，可以对照着练习一下，这样就可以搞懂前序/中序/后序遍历的方式，结合代码，理解具体的实现；

参考

树的遍历

文章来源: great.blog.csdn.net，作者：小麦大叔，版权归原作者所有，如需转载，请联系作者。

原文链接：great.blog.csdn.net/article/details/95768639