分数谐波？

昨天探讨了关于电机PWM的谐波对于电磁传感器的干扰问题。由于PWM的高次谐波会落在20kHz的传感器的通带内，所以需要避免PWM的频率为20kHz的整数分数值。

看到同学的一个留言，提到了关于周期信号的分数次谐波的问题。

从这个留言中，似乎认为对于一个周期方波信号，会产生一个与占空比成比例的分数谐波。这个观点在信号分析中应该是不正确的。

一般情况下，习惯于教授理论的老师就可以直接写出对应的公式来进行分析和说明了，或者将公式绘制成曲线说明信号频谱的分布。考虑到很多同学现在尚未学习信号与系统相关的内容，为了提高大家对于这个问题的兴趣，下面直接利用昨天实验环境，分别测试一下不同的PWM的占空比所产生的干扰频率点的变化。

图1 测量实验环境

昨天的实验结果显示，在20kHz的整数分数（1/2,1/3,1/4,1/5,1/6…）频率处，PWM电机信号都会对传感器噪声干扰。这是由于这些频率的某些整数倍数的谐波会恰好落在20kHz通带范围，当时的PWM波形的占空比为10%.

下面分别取占空比为20%，25%，33%，50%重新测量PWM的频率与干扰信号强度之间的关系。可以保证，下面的所有曲线都是自动采集的实际信号绘制的，绝没有通过公式计算出来的，所以它们反映了真是物理世界中信号的可以测量到的频谱分布。

通过观察会发现，不同的占空比下的PWM信号，并没有产生新的干扰频率点。相反，原来的一些干扰频率点反而消失了。具体的规律看大家是否能够通过测量总结出来？

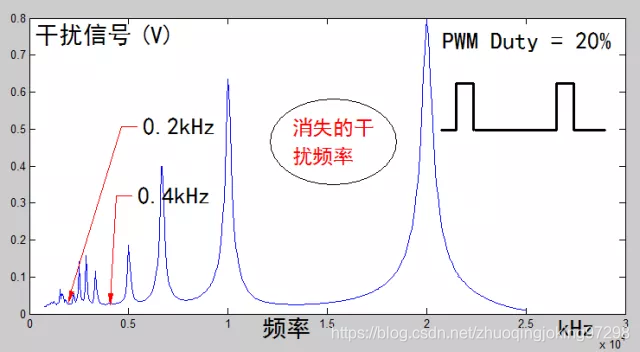
图2 占空比为20%时，PWM信号对传感器的干扰频率点

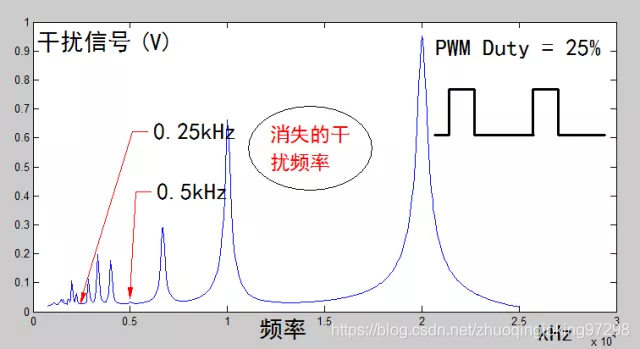
图3 占空比为25%时，PWM信号对传感器的干扰频率点

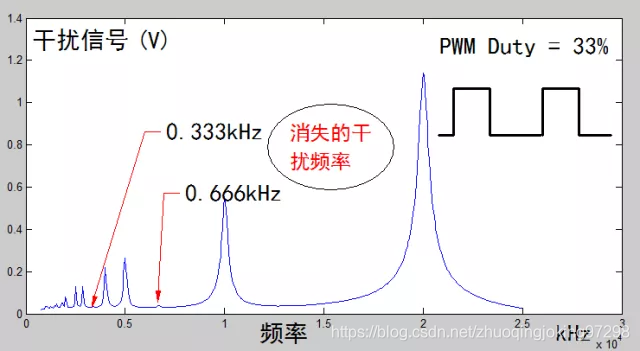
图4 占空比为33%时，PWM信号对传感器的干扰频率点

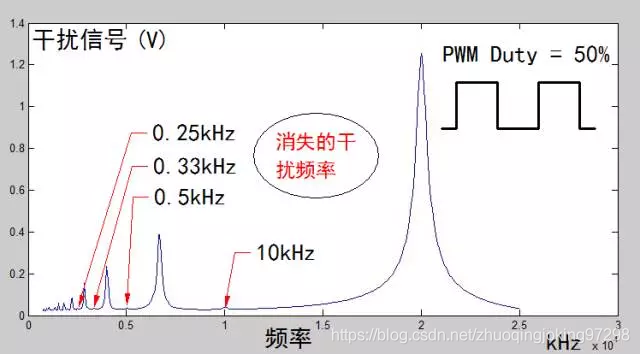
图5 占空比为50%时，PWM信号对传感器的干扰频率点

通过上面的测量的数据可以看出，改变PWM波形的占空比并不会带来新的干扰频率点。相反，原来存在着的频率点会在不同的占空比下消失了。例如，使用1/n的占空比，那么在所有的1/n,1/(2n),1/(3n)等处的干扰频率点都消失了。特别对于占空比为50%（1/2）时，所有的1/2n的干扰频率点都不存在了。

为什么会出现这种情况呢。此处省去3000字的理论推导，直接拿出频谱分析公式就可以说明了。对于一个周期为T，高电平为tao的方波脉冲信号，它的各次谐波的幅度如下图中的公式给出。

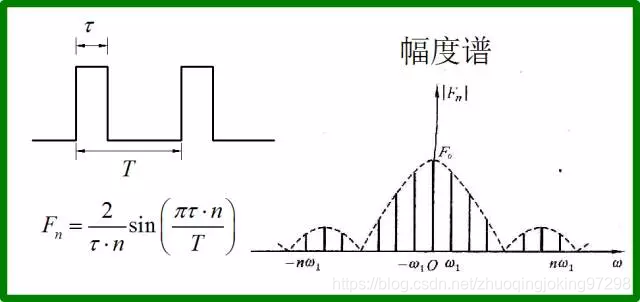
图6 方波脉冲信号频谱分解公式及其幅度谱

可以看出，各次谐波的幅值是由sinc函数决定的。当T是tao的整数倍数的时候，那么位于这些倍数处的谐波幅值都恰好为0。特别是，当tao等于T一半的时候，所有n等于偶数时，对应的谐波幅值都为0。

根据上面的结论，反过来，当PWM的占空比为整数n分之一的时候，对应的20kHz在 1/n, 1/2n, 1/3n等处的PWM信号，它们所对应在20kHz的谐波恰好为零，所以这些频率处的干扰点就消失了。

离开图6中的频谱分解公式，也可以利用信号对称性的关系说明占空比为50%的方波信号中，不存在偶次谐波分量。

信号分解成多个分量的叠加，信号的某种对称性会在分量中加以保持。比如，信号如果是偶对称（或者奇对称），那么它的所有分量也必须是偶函数（或者奇函数）。对称性有很多种，有一种对称性称之为“奇谐对称”。它是指信号的平移半个周期之后，正好与原来信号相反。

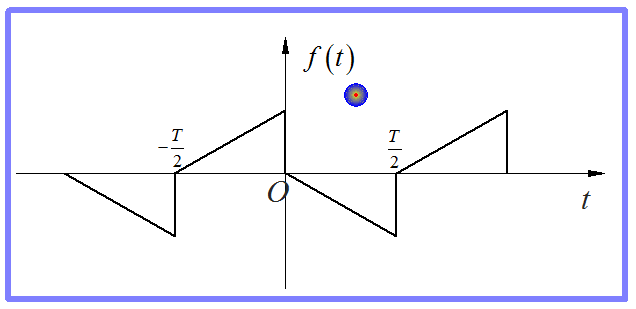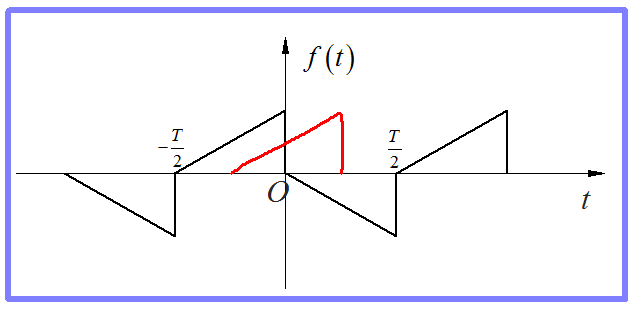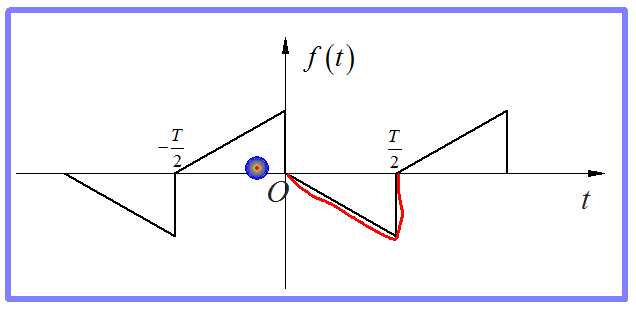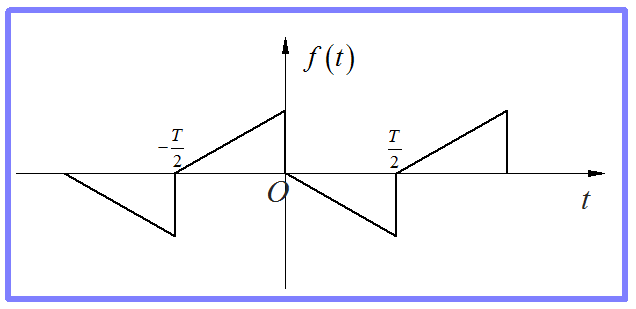
图7 奇谐对称信号

对于正弦信号分析，可以看出上述的奇谐对称关系在正弦波1,3,5…等奇数个周期上也存在。同理，对于余弦波形也是如此。

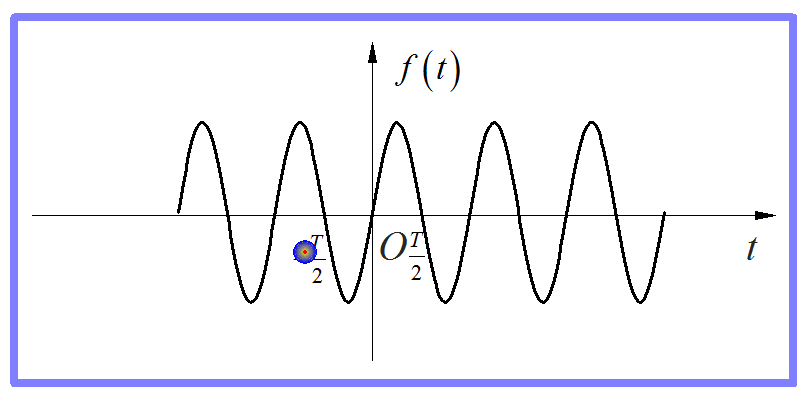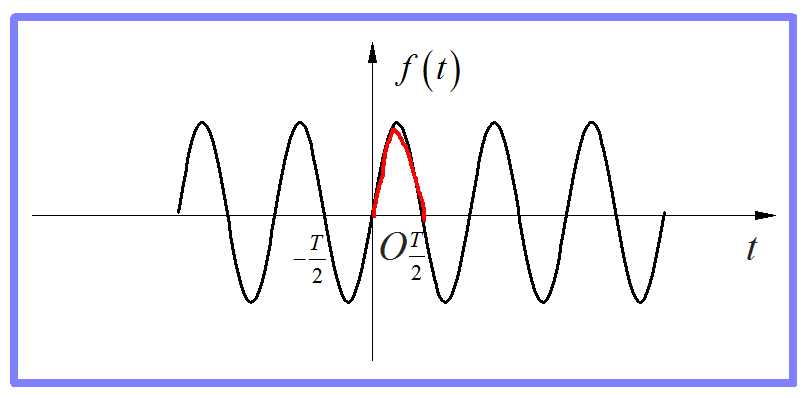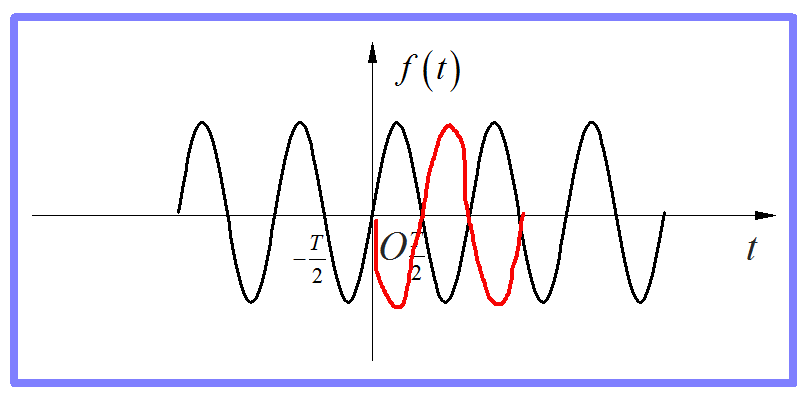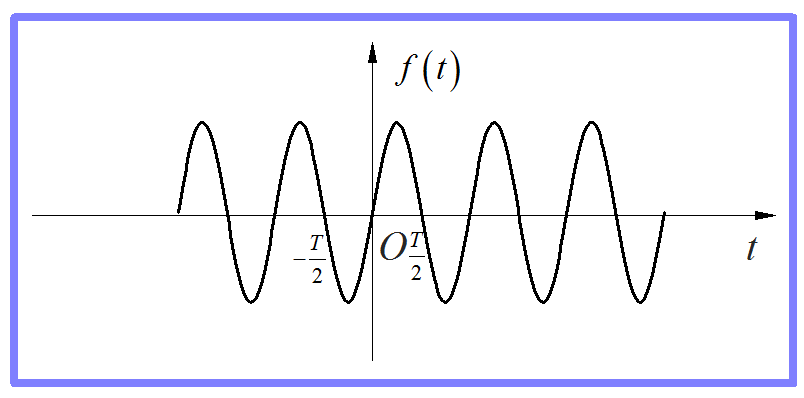
图8 奇次正弦波的奇谐对称

那么，以此就可以得到如下的结论：对于一个奇谐对称的周期信号，它的所有奇次谐波也满足奇谐对称，所以存在。相反，偶次谐波不满足上述的奇谐对称关系，因此就不存在。这也是“奇谐”周期信号的名称的由来。

对于普通的占空比为50%的方波信号，它的交流分量也是一个奇谐信号。除此之外，你们还能够举出那些常见到的信号是“奇谐信号”吗？

对于一个周期信号，它的谐波难道就只能是它的基波频率的整数倍数吗？

在数学上是的确如此。无论这个周期信号长成什么样，它的各个分量就只能是基波频率的整数倍数的离散频谱，绝对不会产生基波频率的分数谐波的。

在实际世界中，严格周期信号是不存在的，特别是对于只存在一定时间的震荡信号，实际上已经不是严格意义上的周期信号了。比如，对于一个周期信号截取其中一段时间的信号，此时，它的频谱就会产生很多新的分量。实际上，此时信号的频谱就会形成一个连续的频谱密度函数。再往下，就会从傅里叶级数分解推导出傅里叶变换的数学分析工具了。

图9 钢琴琴弦的震动存在着高阶分数谐波

除了对于信号截取会产生新的频率之外，如果周期信号经过一个非线性系统，

往往也会产生新的频率，甚至是分数频率。在钢琴乐器中，由于其中存在着大量的谐振单元，相互之间有着相互的耦合以及一些非线性的作用，因此，对于钢琴的发出的单个乐音中，不仅包含着丰富的谐波分量，同时还存在着一一些非整数谐波（分数谐波），这就使得钢琴的声音变得非常丰富多彩。

同样，如果周期信号经过一个时变系统，也会有新的频率信号产生。激光干涉引力波天文台（LIGO）中的激光干涉信号，在平时，除了它本身激光稳定的频率之外，是不会有新的频率信号的。但是当引力波扫过地球时，整个空间的所有参数都会随着时间发生相应的变化，此时激光的频率也同样出现了漂移，从而使得系统输出发生变化了的干涉信号，表明了当前时空由于引力波所产生的变化。

图10 时变的时空也会引起新的频率分量的产生

文章来源: zhuoqing.blog.csdn.net，作者：卓晴，版权归原作者所有，如需转载，请联系作者。

原文链接：zhuoqing.blog.csdn.net/article/details/104120641