信号与系统作业问题回复
提问
老师好!我想请问几个上周作业中的问题。
- 作业第一题第三问中设置的中间变量为什么最后无法消除?实际表达式中可以保留中间变量吗?

第一道题第3小问离散时间系统框图
- 作业第5题的7,8小问中,从响应的表达式r(t)来看,t应该是变化量,而输入信号一侧e(τ)和t却是分开在积分算式的两个位置。那么这时候判断系统性质时输入信号到底是t还是e(τ)呢?
( 7 ) r ( t ) = ∫ − ∞ t e ( τ ) d τ (7)\,\,\,\,\,r\left( t \right) = \int_{ - \infty }^t {e\left( \tau \right)d\tau } (7)r(t)=∫−∞te(τ)dτ
( 8 ) r ( t ) = ∫ − ∞ 5 t e ( τ ) d τ (8)\,\,\,\,r\left( t \right) = \int_{ - \infty }^{5t} {e\left( \tau \right)d\tau } (8)r(t)=∫−∞5te(τ)dτ
- 作业最后一题中,多个系统级联,那么计算时输入下一级系统中的信号应该是x[n]中的n,还是x[n]整体呢?(换句话说,就是对于输入信号,应当把x[n]整体看做一个变量,还是把n看做一个变量呢?)

三个子系统的输入输出关系

三个子系统的串联关系
问题有些多,麻烦老师了……
回复
第一个问题
对于第一道题第三小问中离散时间系统框图,带有两个综合器(加法器)。因此建立该系统输入输出差分方程的时候,需要将中间的节点设置临时变量。假设第一个综合器的输出的临时变量为w[n],那么它后面两个延时单元之后的节点临时变量分别是w[n-1],w[n-2]。
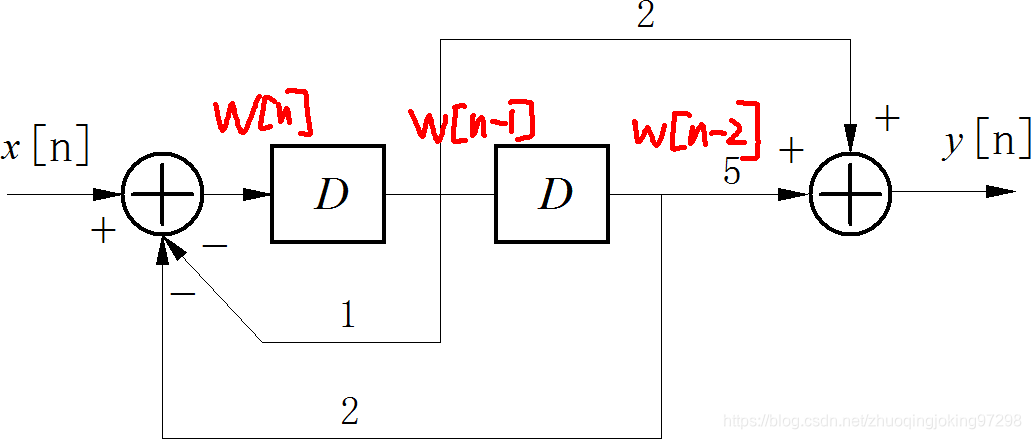
对系统框图的两个综合器中间的节点设置临时变量
由此可以根据第一个加法器(综合器)建立x[n]与w[n]之间的差分方程:
x [ n ] = w [ n ] + w [ n − 1 ] + 1 2 w [ n − 2 ] x\left[ n \right] = w\left[ n \right] + w\left[ {n - 1} \right] + {1 \over 2}w\left[ {n - 2} \right] x[n]=w[n]+w[n−1]+21w[n−2]
根据第二个加法器建立y[n]与w[n]之间的差分方程:
y [ n ] = 2 w [ n − 1 ] + 5 w [ n − 2 ] y\left[ n \right] = 2w\left[ {n - 1} \right] + 5w\left[ {n - 2} \right] y[n]=2w[n−1]+5w[n−2]
下面将上面两个方程中的临时变量消去,获得x[n]与y[n]之间的差分方程。为了简便起见,我们使用“延时算子”来将上面两个差分方程修改成算子代数方程组:
x [ n ] = ( 1 + D + 1 2 D 2 ) w [ n ] {x\left[ n \right] = \left( {1 + D + {1 \over 2}D^2 } \right)w\left[ n \right]} x[n]=(1+D+21D2)w[n]
y [ n ] = ( 2 D + 5 D 2 ) w [ n ] {y\left[ n \right] = \left( {2D + 5D^2 } \right)w\left[ n \right]} y[n]=(2D+5D2)w[n]
将上面两个算子代数方程相除,可以得到:
x [ n ] y [ n ] = 1 + D + 1 2 D 2 2 D + 5 D 2 {{x\left[ n \right]} \over {y\left[ n \right]}} = {{1 + D + {1 \over 2}D^2 } \over {2D + 5D^2 }} y[n]x[n]=2D+5D21+D+21D2
因此:
( 2 D + 5 D 2 ) x [ n ] = ( 1 + D + 1 2 D 2 ) y [ n ] \left( {2D + 5D^2 } \right)x\left[ n \right] = \left( {1 + D + {1 \over 2}D^2 } \right)y\left[ n \right] (2D+5D2)x[n]=(1+D+21D2)y[n]
由此可得:
y [ n ] + y [ n − 1 ] + 1 2 y [ n − 2 ] = 2 x [ n − 1 ] + 5 x [ n − 2 ] y\left[ n \right] + y\left[ {n - 1} \right] + {1 \over 2}y\left[ {n - 2} \right] = 2x\left[ {n - 1} \right] + 5x\left[ {n - 2} \right] y[n]+y[n−1]+21y[n−2]=2x[n−1]+5x[n−2]
通过设置中间临时变量,是可以将中间变量消去。在最后的答案中,应该只包含有系统的输入x[n]和输出y[n]信号以及它们的各阶延迟信号,构成后向差分方程。
第二个提问:
在第五题的(7),(8)小题中描述系统输入输出关系的表达式中, e ( t ) e(t ) e(t) 是系统输入信号。 r ( t ) r(t) r(t) 是系统输出信号。表达式表示系统的输出是对输入信号e(t)的积分。
( 7 ) r ( t ) = ∫ − ∞ t e ( τ ) d τ (7)\,\,\,\,\,r\left( t \right) = \int_{ - \infty }^t {e\left( \tau \right)d\tau } (7)r(t)=∫−∞te(τ)dτ
( 8 ) r ( t ) = ∫ − ∞ 5 t e ( τ ) d τ (8)\,\,\,\,r\left( t \right) = \int_{ - \infty }^{5t} {e\left( \tau \right)d\tau } (8)r(t)=∫−∞5te(τ)dτ
在积分表达式中,变量 τ \tau τ是积分变量,变量 t t t 是积分的上限,也就是积分运算的参数。最终积分结果是参数 t t t 的函数。这就是系统的输出。
在你的提问中,似乎将信号 e ( t ) e(t) e(t) 的描述与信号的自变量 t t t 混淆了。在积分始终,将 e ( t ) e(t) e(t) 写成 e ( τ ) e\left( \tau \right) e(τ),是因为积分变量是 τ \tau τ。
补充一下,对于第8小题,可以看出系统是由两个子系统串联而成,第一个子系统就是积分系统,也就是第7小题描述的系统,然后紧跟着一个尺度变化系统:将输入信号压缩5倍。

第8小题的等价系统框图
第三个提问
我仔细揣摩你提问时心里的 疑问,对于子系统串联时,输入信号是 x [ n ] x[n] x[n] 的整体,还是具体到一个个单独的 n 所对应的 一个数值 x[n]。
我认为这两个中想法应该都对。
如果将x[n]当做整体通过三个子系统,那就是将整个系统对输入信号的处理分成了三步:
第一步,将x[n]送入第一个子系统,按照题目中给定的描述,是将输入信号通过补零扩充两倍;
第二步将处理扩充完毕的结果在送入第二个子系统,按照题目中对第二个子系统的描述,就是对第一个子系统的输出以及它的两个延迟信号进行加权累加;
第三步将子系统2 的输出在送入第三个子系统,即在重新抽点压缩。
最后子系统3所得到的输出应该是:
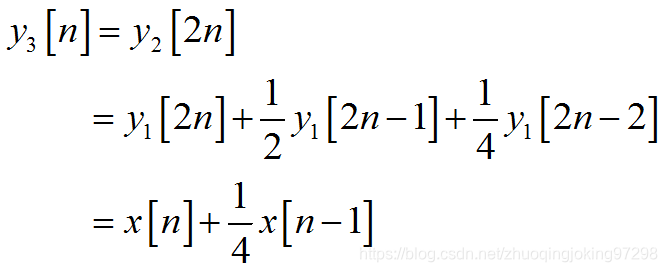
子系统3的输出
这是整个系统的输出与输入x[n]之间的关系。它们应该是一个线性时不变的关系。
但是在实际系统运行过程中,信号是逐步通过三个子系统。这三个子系统是离散时间系统,它们同步进行协同工作。由于其中存在着对信号的扩充和压缩,因此,它们工作的时钟频率会有差别。
第一个子系统的工作频率和第二个子系统是相同的,由于第一个子系统是数据补零扩充,所以它们的输出数据速率都是输入数据x[n]速率的两倍。
第三个子系统由于是压缩,所以它的输出数据的速率是前面两个子系统速率的一半,也就是与输入信号的速率相同。
最终系统的输入输出关于与前面整体分析的结果是一样的。
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/104644907
- 点赞
- 收藏
- 关注作者




评论(0)