信号建模与参数估计作业重新计算
问题的缘起
在下面博文中,记录了在2020春季学期第二次作业中的MATLAB实验作用中 的问题。
通过示波器数据进行正弦信号参数估计
下面的电路中:

测量RC电路
根据电路原理,可以知道上述电路稳态输入输出正弦信号之间的关系如下:
V ˙ = 1 j 2 π f C 1 R 1 + 1 j 2 π f C 1 U ˙ = 1 1 + j 2 π f R 1 C 1 U ˙ \dot V = {{{1 \over {j2\pi fC_1 }}} \over {R_1 + {1 \over {j2\pi fC_1 }}}}\dot U = {1 \over {1 + j2\pi fR_1 C_1 }}\dot U V˙=R1+j2πfC11j2πfC11U˙=1+j2πfR1C11U˙
因此,输入输出正弦信号的幅度之比为:
α = ∣ V ˙ ∣ ∣ U ˙ ∣ = 1 1 + ( 2 π f R C ) 2 \alpha = {{\left| {\dot V} \right|} \over {\left| {\dot U} \right|}} = {1 \over {\sqrt {1 + \left( {2\pi fRC} \right)^2 } }} α=∣∣∣U˙∣∣∣∣∣∣V˙∣∣∣=1+(2πfRC)21
输入输出正弦信号的相位差为: θ \theta θ tan ( θ ) = 2 π f ⋅ R C \tan \left( \theta \right) = 2\pi f \cdot RC tan(θ)=2πf⋅RC
所以,只要能够测量出U,V两个正弦信号的幅度或者相位,频率,再加上已知电阻阻值R\1.,便可以计算出来待测电容的容值。
C = tan θ 2 π f ⋅ R = 1 − α 2 α ⋅ 1 2 π f ⋅ R C = {{\tan \theta } \over {2\pi f \cdot R}} = {{\sqrt {1 - \alpha ^2 } } \over \alpha } \cdot {1 \over {2\pi f \cdot R}} C=2πf⋅Rtanθ=α1−α2⋅2πf⋅R1
因此,如果根据同一组 R C RC RC 参数,在上面公式中两个比例因子 tan ( θ ) \tan \left( \theta \right) tan(θ) 和 1 − α 2 α {{\sqrt {1 - \alpha ^2 } } \over \alpha } α1−α2 应该相同,即:
tan ( θ ) = 1 − α 2 α \tan \left( \theta \right) = {{\sqrt {1 - \alpha ^2 } } \over \alpha } tan(θ)=α1−α2
但实际根据测量数据,经过正弦曲线拟合会发现,这两个数值相差很大:

MATLAB计算出的参数的问题
这也就使得通过相位和幅值比这两个方法最终估计出来的电容C的容值也相差近一倍。这是为什么呢?
最后还是猜测,可能在原始数据中存在错误。下面重新再进行实验一次。
重新实验
实验方式
在面包板上搭建RC低通滤波器的电路,并使用STNFORDDS345信号源加以激励,使用RIGOL DS6104获得输入输出的数据。

实验面包板上的实验电路
实验参数设置
按照前面作业中的参数其中:
-
电阻取值: R= 1 k Ω 1k\Omega 1kΩ。
-
电容: C = 0.1 μ F C = 0.1\mu F C=0.1μF
-
驱动信号:频率:400Hz,
幅值:2V

测量电容所使用的手持LCR表
实验过程
(1)使用DS6104 采集方式设置为Normal,采集测到的波形:
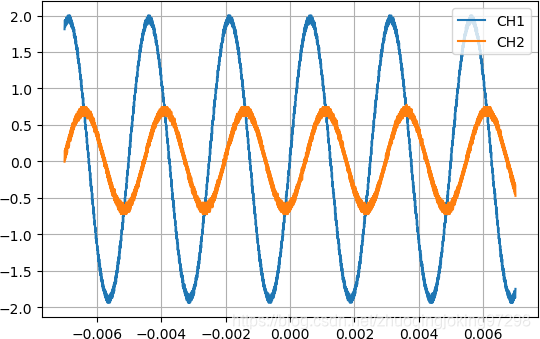
使用Normal采集方式所获得的示波器的波形
在Normal数据采集中,实际数值是示波器采集多次之后将它们的数值的上限和下限进行显示,并不是一次采样的值。
因此将示波器的显示值重新设置为High Resolution,这样显示的数值就是在一次采集后波形数值了。
从下面的波形可以看出,信号波形“细”了。这实际上就是一次波形采样的数据对应的波形。
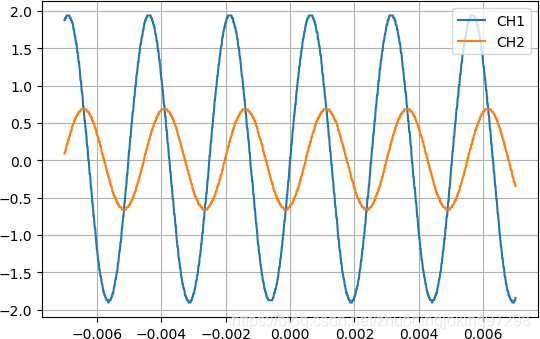
使用High Res采集方式所获得的示波器的波形
数据采集Python程序为:
from tsmodule.tsvisa import *
ds6104open()
#------------------------------------------------------------
x, y1, y2 = ds6104readcal(1, 2)
plt.plot(x, y1, label='CH1')
plt.plot(x, y2, label='CH2')
plt.legend(loc='upper right')
plt.grid(True)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
采集数据以及数据分析
使用在前面博文分析的Python程序,获得两个数据曲线的下面参数:
其中第一个是:频率,第二个是直流分量,第三个是正弦波的峰值;第四个是相位。
[ 3.98166407e+02 2.53299752e-02 1.91818740e+00 -3.13791632e-02]
[ 3.98158934e+02 1.51520273e-02 6.73493167e-01 -1.24122570e+00]
-2.6490936925544855
2.6667903893157003
- 1
- 2
- 3
- 4
- 5
由此可见两个信号的估计频率都基本上是 f = 398.2 H z f = 398.2Hz f=398.2Hz,与实际信号源设置的400Hz相差0.5%。
根据估计的参数重新绘制波形,它们与测量波形重叠。这说明估计的参数符合测量数据。
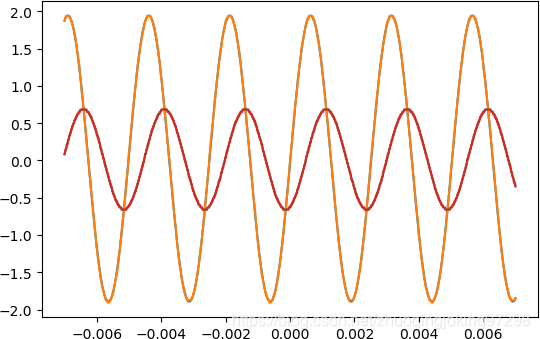
将估计的参数重新绘制波形
按照上面估计参数,两个正弦波的数学表达式应该为:
f i n ( t ) = 0.0253 + 1.918 sin ( 2 ⋅ π ⋅ f − 0.0314 ) f_{in} \left( t \right) = 0.0253 + 1.918\sin \left( {2 \cdot \pi \cdot f - 0.0314} \right) fin(t)=0.0253+1.918sin(2⋅π⋅f−0.0314)
f o u t ( t ) = 0.0151 + 0.6735 sin ( 2 ⋅ π ⋅ f − 1.2412 ) f_{out} \left( t \right) = 0.0151 + 0.6735\sin \left( {2 \cdot \pi \cdot f - 1.2412} \right) fout(t)=0.0151+0.6735sin(2⋅π⋅f−1.2412)
由此可得到:
α = ∣ V o u t ∣ ∣ V i n ∣ = 0.6735 1.918 = 0.35115 \alpha = {{\left| {V_{out} } \right|} \over {\left| {V_{in} } \right|}} = {{0.6735} \over {1.918}} = 0.35115 α=∣Vin∣∣Vout∣=1.9180.6735=0.35115
1 − α 2 α = 2.667 {{\sqrt {1 - \alpha ^2 } } \over \alpha } = 2.667 α1−α2=2.667
根据两个信号的相位差,则:
Δ θ = 0.0314 − ( − 1.2412 ) = 1.2726 \Delta \theta = 0.0314 - \left( { - 1.2412} \right) = 1.2726 Δθ=0.0314−(−1.2412)=1.2726
tan ( Δ θ ) = 2.6491 \tan \left( {\Delta \theta } \right) = 2.6491 tan(Δθ)=2.6491
由此可见,使用两个公式中的比例因子基本相同了。
tan ( Δ θ ) = 1 − α 2 α \tan \left( {\Delta \theta } \right) = {{\sqrt {1 - \alpha ^2 } } \over \alpha } tan(Δθ)=α1−α2
由此可见在保证同样的RC参数,以及输入频率下,这两个参数应该和理论分析一样,是相同的。
结论
通过重新采集数据,验证了RC低通滤波器,使用相同的RC参数,在相同的激励信号的频率下,通过相位和幅值进行测试RC参数,最终所得到的数值应该是相同的。
至于为什么最初作业所测量得到的数据有误,现在就不得而知了。
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/104682737
- 点赞
- 收藏
- 关注作者


评论(0)