时间采样
近期在信号与系统课程讲完了“信号的采样与恢复”的内容。通常情况下对于信号的采样都是沿着时间轴对信号的幅值进行采样,获得信号的离散时间点上的数据。
如果将信号 s ( t ) s\left( t \right) s(t)的波形绘制在直接坐标系中,那么该曲线就是分布在二维空间上的曲线。曲线上的点可以沿着时间 t t t轴进行排列,当然也可以按照幅值 s ( t ) s\left( t \right) s(t)的大小进行排列。也就是按照取值间隔,将信号通过该间隔的时间进行保存,这就是对信号的时间采样。

▲ 声音的时间波形
沿着时间轴对信号的幅值进行采样,Nyquist-Shannon定理告诉我们如何进行采样和如何进行信号恢复。但是,如何对信号时间进行采样,如何恢复是一个经典的未解决问题。
Logan定理[Logan,Jr.,1977]对一种特殊信号给出了采样与恢复的描述:如果一个信号的频谱具有倍频的性质,即信号频谱分布在一个频率范围内,最高频率是最低频率的两倍。那么这个信号可以通过它的过零点的时间值进行恢复。恢复的信号与原始信号仅仅相差一个比例因子。
信号采样与恢复
1. 幅度采样
下面是一段普通语音信号的复制采样波形。通过简单的DA转换和低通滤波便可以恢复出原始的声音波形。

▲ 幅度采集声音波形
2. 时间采样
如果仅仅保留该信号的过零时间点的信息,它的幅值全部去掉,所形成的波形大体上如下图所示。这很像将原来的语音信号通过一个过零点比较器,输出的信号反映了信号的极性。
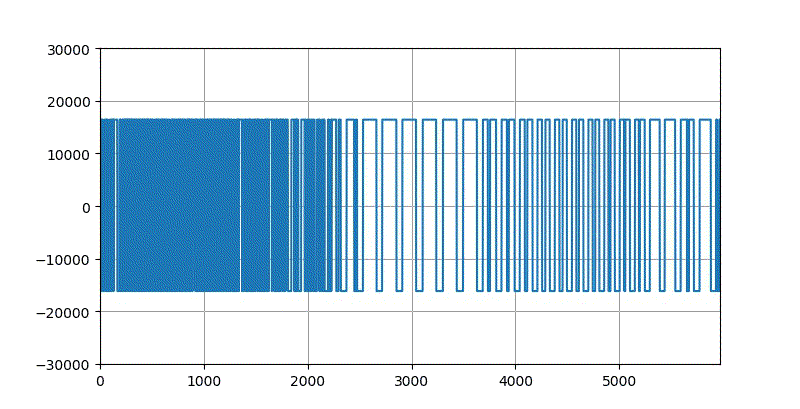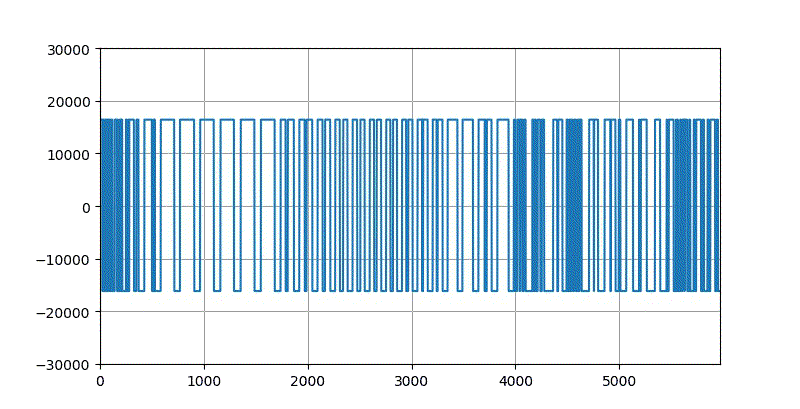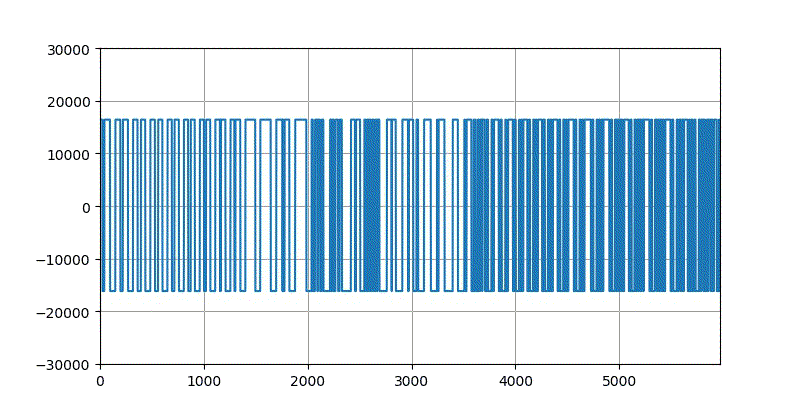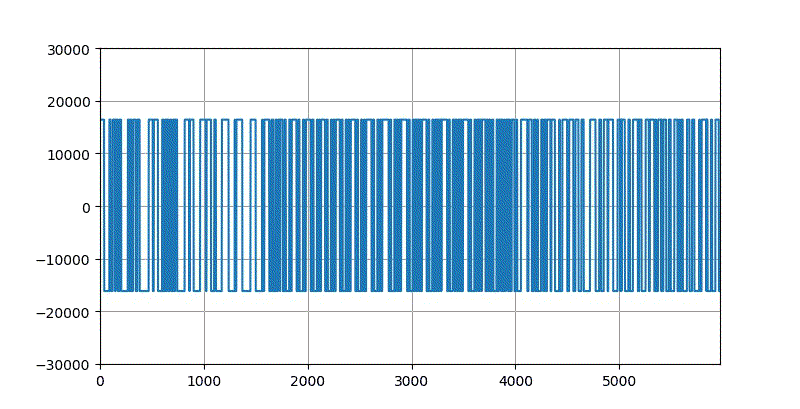
▲ 声音信号过零点采样
当然,这个信号中包含有原来信号的部分信息。但它并不是原来语音信号的完美的回复。
尽管如此,播放这个信号,还是可以听到原来语音的信息。虽然有很大的失真和噪声。这说明原来的信号信息还是部分保留在这些过零点中。
如果语音信号满足Logan定理的要求,那么理论上是可以恢复出原来的信号的。但如何来恢复?
如果信号本身是一个周期信号,也就是信号的频谱是离散的频谱。相对回复信号的算法比较简单。Sam Roweis等人在论文“Signal Reconstruction from Zero-Crossings"中给出了通过求解数据矩阵零空间向量的方法,来通过信号的过零时间点来重构信号的方法。
重建算法
1. 基本原理
已知到信号 s ( t ) s\left( t \right) s(t)具有倍频窄带频谱,它的频率范围分布在 [ f min , 2 f min ] \left[ {f_{\min } ,2f_{\min } } \right] [fmin,2fmin]范围内。

▲ 倍频信号频谱示意图
已知信号的周期 T T T, f min f_{\min } fmin,以及 N N N个信号过零点: Z t = { t 1 , . . . , t j , . . . , t N } Z_t = \left\{ {t_1 ,...,t_j ,...,t_N } \right\} Zt={t1,...,tj,...,tN}
重构信号的计算步骤如下:
(1)计算相关参数: f 0 = 1 / T f_0 = 1/T f0=1/T以及 f k , k = 1... M f_k ,k = 1...M fk,k=1...M;
(2)构造矩阵: X j k = 2 π t j f k X_{jk} = 2\pi t_j f_k Xjk=2πtjfk;
(3)寻找数据矩阵零空间向量:
构造数据矩阵 [ cos ( X ) , sin ( X ) ] \left[ {\cos \left( X \right),\sin \left( X \right)} \right] [cos(X),sin(X)],矩阵大小是 N × 2 M N \times 2M N×2M。对该矩阵进行奇异值分解,得到 U , V , σ U,V,\sigma U,V,σ。其中 U U U是 R N R^N RN空间上的正交矩阵, V V V是 R 2 M R^{2M} R2M空间上的正交矩阵。 σ \sigma σ是奇异值向量,长度为 min ( N , 2 M ) \min \left( {N,2M} \right) min(N,2M)。
零空间向量是奇异值向量 σ \sigma σ中最小(理论上应该为0,但由于计算误差的存在,它可能是一个很小的数)对应的 V V V中的向量,由于SVD算法往往把结果 σ \sigma σ按照绝对值从大到小排列,所以 V V V的最后一个向量就对应着数据矩阵的零空间向量。
(4)构造信号函数:
将数据空间矩阵中零空间向量前 M M M个数值当做 a ^ k \hat a_k a^k,后 M M M个数值当做 b ^ k \hat b_k b^k,重建信号公式为: s ^ ( t ) = ∑ k = 1 M [ a ^ k cos ( 2 π f k t ) + b ^ k sin ( 2 π f k t ) ] \hat s\left( t \right) = \sum\limits_{k = 1}^M {\left[ {\hat a_k \cos \left( {2\pi f_k t} \right) + \hat b_k \sin \left( {2\pi f_k t} \right)} \right]} s^(t)=k=1∑M[a^kcos(2πfkt)+b^ksin(2πfkt)]
这种回复信号的过程,实际上就是根据信号的过零点来求解上面的函数中的参数。具体的理论分析在这里就不再展开了。
2. 测试函数
(1)实验信号的数学表达式:
选择一个频率分布在10Hz到20Hz之间的一个信号进行实验,随机指定对应的cos,sin信号的系数,如下:

▲ 信号的数学表达式
这是一个周期为1的倍频信号。
(2)信号的产生Python程序:
使用下面python程序,可以产生该信号的数据。也可以通过该函数完搜索信号的过零点。
def sfunc1(x):
pi2 = 2 * pi
retdata = cos(pi2*11*x) + sin(pi2*11*x)/2 + \
cos(pi2*12*x)/33 + sin(pi2*12*x)/4 + \
cos(pi2*13*x) + sin(pi2*13*x)/8 + \
cos(pi2*14*x) + sin(pi2*14*x)/7 + \
cos(pi2*15*x)/22 + sin(pi2*15*x)/3 +\
cos(pi2*16*x) + sin(pi2*16*x)/12 +\
cos(pi2*17*x) + sin(pi2*17*x)/40 +\
cos(pi2*18*x) + sin(pi2*18*x)/2 +\
cos(pi2*19*x)/3 + sin(pi2*19*x)/2
return retdata
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
(3)实验信号的波形:
下面绘制出0~2秒两个周期内的波形。

▲ 测试函数sfunc1信号波形
绘制该信号的过零点饱和信号,它仅仅保留了该信号的过零点的时间和相位信息。计算公式为: s 1 ( t ) = s g n [ s ( t ) ] × 2 − 1 s_1 \left( t \right) = {\mathop{\rm sgn}} \left[ {s\left( t \right)} \right] \times 2 - 1 s1(t)=sgn[s(t)]×2−1

▲ 该信号的幅值饱和信号
(4)信号的过零点:
通过数值计算,来获得信号的过零点。下面重新绘制出信号一个周期内的波形,没有添加任何噪声。

▲ 一个周期(0~1)之间的信号波形
通过对区间(0,1)采集106个数值,然后通过寻找过零点,获得二十八个信号的过零点的值:
[0.020366020366020365, 0.05264605264605264, 0.08225308225308224, 0.10514510514510514, 0.12902412902412902, 0.15825015825015823, 0.18724018724018723, 0.2127262127262127, 0.23897923897923895, 0.2701412701412701, 0.3053293053293053, 0.34866534866534865, 0.3915033915033915, 0.4291844291844291, 0.46993546993546986, 0.5351945351945352, 0.5752205752205751, 0.6136616136616136, 0.6501956501956502, 0.6852306852306852, 0.717056717056717, 0.7439707439707439, 0.7804877804877804, 0.8177278177278177, 0.8532438532438532, 0.9194179194179193, 0.9536469536469535, 0.9872359872359872]
搜寻函数值过零点的python程序如下crosszero(t,val)。其中 t t t是函数的自变量, v a l val val是函数值的采样。函数返回是对应函数过零点时的 t t t的数值。
def crosszero(t, val):
valsign = sign(val)
valsignchange = [int(x!=y) for x,y in zip(valsign[0:-1],valsign[1:])]
tvalue = [(x,y) for x,y in zip(t[0:-1], valsignchange)]
zerot = filter(lambda t: t[1]!= 0, tvalue)
return [zt[0] for zt in zerot]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
通过scipy.optimize.root来寻找信号的根,用于确定信号的过零点。利用上面搜索的结果作为初始值。
sol = scipy.optimize.root(tssub.sfunc1, czt, method='lm')
- 1
- tssub.sfunc1:定义的信号函数;
- czt:是前面通过数值过零点搜索获得的28个根的数值;
如下是sol[‘x’]中的数值,包含了最终优化后的数值,对比前面通过搜索获得数值,可以看到基本上在10-6的内存在一定的误差。
[0.02036688 0.05264705 0.082254 0.10514582 0.12902459 0.15825048
0.18724039 0.21272638 0.2389802 0.27014134 0.30532965 0.34866578
0.39150363 0.42918453 0.46993606 0.5351952 0.57522075 0.61366181
0.65019586 0.68523072 0.71705679 0.74397169 0.78048871 0.81772859
0.85324476 0.91941802 0.95364771 0.98723646]
将通过数值计算所得到的28个函数的根绘制在信号波形上,看到他们的分布。

▲ 寻找到的信号过零点
3. 重建结果
根据前面所叙述的方法,使用28个过零点信息重构出的信号波形如下图所示。重构的信号与原始的信号之间波形基本一致,只是相差了一个比例因子。

▲ 重建的波形结果
重构的Python程序如下所示:
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TSTEST2.PY -- by Dr. ZhuoQing 2020-04-20
#
# Note:
#============================================================
from headm import *
sol = tspload('root1000000', 'sol')[newaxis]
printf(sol)
#------------------------------------------------------------
T = 1 # Funcntion period
f0 = 10
f1 = 20
fk = linspace(f0, f1, int((f1 - f0) / T), endpoint=False)[newaxis]
printf(fk)
#printf(type(fk))
Xjk = 2 * pi * sol.T * fk
printf(shape(Xjk))
CosX = cos(Xjk)
SinX = sin(Xjk)
CSinX = concatenate((CosX, SinX), axis=1)
#------------------------------------------------------------
u,s,v = linalg.svd(CSinX)
zs = v[-1]
#------------------------------------------------------------
t = linspace(0, 1, 10000)
a = zs[0:int(len(zs)/2)]
b = zs[int(len(zs)/2):]
#------------------------------------------------------------
fr = zeros(size(t))
k = list(range(size(fk)))
for id,ak,bk in zip(k,a,b):
printff(id,ak,bk)
fr = fr + ak*cos(2*pi*fk[0][id]*t) + bk*sin(2*pi*fk[0][id]*t)
plt.plot(t, fr)
plt.xlabel('Time(s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.show()
#------------------------------------------------------------
# END OF FILE : TSTEST2.PY
#============================================================
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
辅助程序
1. 将WAV文件转换成ClipVoice文件。
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# CLIPVOICE.PY -- by Dr. ZhuoQing 2020-04-19
#
# Note:
#============================================================
from headm import *
import wave
#============================================================
voicefile = r'd:\temp\voice2.wav'
voicedata = wave.open(voicefile, 'rb')
frames = voicedata.getnframes()
params = voicedata.getparams()
printff(frames, params)
voiceframe= voicedata.readframes(frames)
#------------------------------------------------------------
def voice2lr(data):
dataint = [(lambda x:-(x&0x8000)+(x&0x7fff))(x+y*256) for x,y in zip(data[0::2],data[1::2])]
return dataint[0::2], dataint[1::2]
datal, datar = voice2lr(voiceframe)
#------------------------------------------------------------
clipvalue = 8000
def wave2clip(data):
clip = []
for id, d in enumerate(data):
if d >= 0:
num = clipvalue
else: num = 0x10000 - clipvalue
clip.append(num)
return clip
dataunsigned = wave2clip(datal)
wavea = [(int(d/0x100), int(d%0x100)) for d in dataunsigned]
wavebytes = bytes([y for x in wavea for y in x])
#------------------------------------------------------------
wavefile = wave.open(r'd:\temp\clipvoice2.wav', 'wb')
wavefile.setparams((1, 2, params[2], frames, 'NONE', 'TsingHua'))
wavefile.writeframes(wavebytes)
wavefile.close()
#------------------------------------------------------------
# END OF FILE : CLIPVOICE.PY
#============================================================
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/105572008
- 点赞
- 收藏
- 关注作者


评论(0)