2020人工神经网络第一次作业-参考答案第六部分

举报
tsinghuazhuoqing 发表于 2021/12/26 22:27:51 2021/12/26
【摘要】 本文是 2020人工神经网络第一次作业 的参考答案第六部分   ➤06 第六题参考答案 1.题目分析 按照题意，构造如下的神经网络。 隐层的传递函数使用sigmoid函数，输出层的...

本文是 2020人工神经网络第一次作业 的参考答案第六部分

 

➤06 第六题参考答案

1.题目分析

按照题意，构造如下的神经网络。

隐层的传递函数使用sigmoid函数，输出层的传递函数采用线性传递函数。

▲ 网络结构

▲ 网络结构

2.网络训练

训练网络，使用学习速率 η = 0.5 \eta = 0.5 η=0.5。▲ 训练过程中样本4对应的输出值变化

▲ 训练过程中样本4对应的输出值变化

▲ 网络训练误差变化曲线

▲ 网络训练误差变化曲线

  • 训练最后误差：0.25

  • 每个样本对应网络输出：

样本 y1 y2 y3 y4
(0,0,0,1) 0.00711268 -0.00986973 0.00305476 0.9998889
(0,0,1,0) -0.135094 0.18961148 0.9424817 0.0030109
(0,1,0,0) 0.44530554 0.37495184 0.18958372 -0.00994176
(1,0,0,0) 0.68266432 0.44529483 -0.13513126 0.0070307
  • 样本对应的隐层输出：
样本 h1 h2
(0,0,0,1) 0.35826803 0.7780322
(0,0,1,0) 0.83654076 0.43139191
(0,1,0,0) 0.38627118 0.26445842
(1,0,0,0) 0.19393638 0.20481963

训练结果显示，对于样本1,2可以基本准确恢复；样本3,4恢复误差较大。

3.隐层节点采用三个

隐层节点数量提高到3个，训练网络，最终网络训练误差可以迅速降低到0。

▲ 网络结构

▲ 网络结构

对于不同样板网络输出：

样本 y1 y2 y3 y3
[0 0 0 1] -0.000 -0.000 -0.000 1.000
[0 0 1 0] -0.000 -0.000 1.000 -0.000
[0 1 0 0] -0.000 0.999 -0.000 -0.000
[1 0 0 0] 1.001 0.001 0.001 0.001

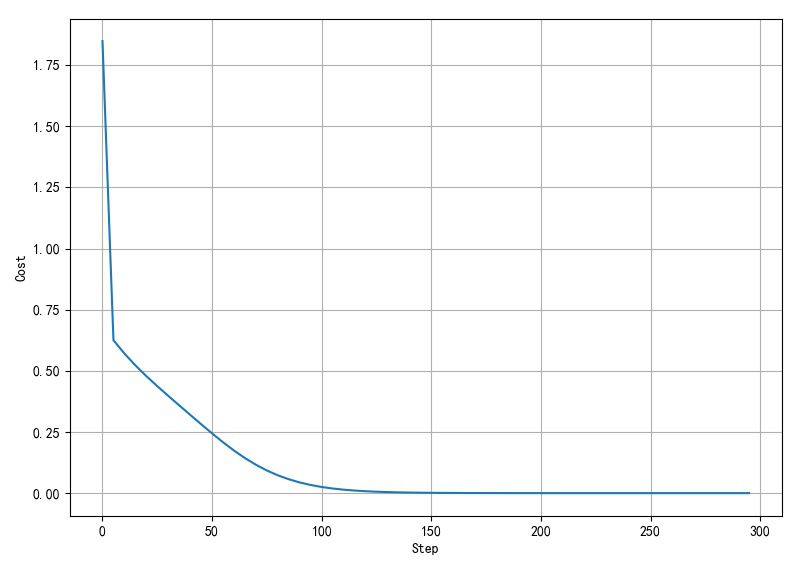
▲ 训练误差演变过程

▲ 训练误差演变过程

▲ 样本四输出值演变过程

▲ 样本四输出值演变过程

4.训练样本增加噪声

对原来四个样本增加正态分布随机噪声（零均值0，方差：0.1）。将训练样本从原来的的四个，扩增到504。
神经网络隐层节点设置为2，重新训练网络。

▲ 网络误差收敛过程

▲ 网络误差收敛过程

四个样本对应的网络输出为：

样本 y1 y2 y3 y3
[0. 0. 0. 1.] 0.327 -0.241 0.218 0.712
[0. 0. 1. 0.] -0.240 0.169 0.849 0.212
[0. 1. 0. 0.] 0.259 0.808 0.171 -0.252
[1. 0. 0. 0.] 0.656 0.267 -0.239 0.327

如果使用0.5作为阈值产地网络的输出重新二值化，可以看到四个样本可以本准确回复。

※ 结论

  1. 对于隐层节点为2的压缩网络，训练输出存在较大的误差；
  2. 将隐层节点增加到3，网络输出误差接近于0；
  3. 对于训练样本通过随机扩增，可以改善网络的输出。重新对输出值进行二值化，可以将恢复误差降低到0.

 

➤※ 作业1-6程序

1.作业1-6的主程序

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# HW16BP.PY                    -- by Dr. ZhuoQing 2020-11-19
#
# Note:
#============================================================

from headm import *
#from bp1tanh               import *
from bp1sigmoid             import *

#------------------------------------------------------------
x_train0 = array([[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]])
#y_train = x_train.T

x_train = [[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]]

EXTEND_NUM = 500
SIGMA = 0.1
for i in range(EXTEND_NUM):
    x_train.append(x_train[0] + random.normal(0, SIGMA, 4))
    x_train.append(x_train[1] + random.normal(0, SIGMA, 4))
    x_train.append(x_train[2] + random.normal(0, SIGMA, 4))
    x_train.append(x_train[3] + random.normal(0, SIGMA, 4))

x_train = array(x_train)
y_train = x_train.T

#------------------------------------------------------------
# Define the training
DISP_STEP           = 5

#------------------------------------------------------------
pltgif = PlotGIF()

y1dim = []
y2dim = []
y3dim = []
y4dim = []

#------------------------------------------------------------
def train(X, Y, num_iterations, learning_rate, print_cost=False):
    n_x = 4
    n_y = 4
    n_h = 2

    lr = learning_rate

    parameters = initialize_parameters(n_x, n_h, n_y)
    XX,YY = x_train, y_train #shuffledata(x_train, y_train)

    costdim = []

    for i in range(0, num_iterations):
        A2, cache = forward_propagate(XX, parameters)
        cost = calculate_cost(A2, YY, parameters)
        grads = backward_propagate(parameters, cache, XX, YY)
        parameters = update_parameters(parameters, grads, lr)

        if print_cost and i % DISP_STEP == 0:
            printf('Cost after iteration:%i: %f'%(i, cost))
            costdim.append(cost)

#            printf(A2.T, cache['A1'].T)

#            XX,YY = shuffledata(X, Y)

            y1dim.append(A2[0][0])
            y2dim.append(A2[1][0])
            y3dim.append(A2[2][0])
            y4dim.append(A2[3][0])

            plt.clf()
            plt.plot(y1dim, label='y1')
            plt.plot(y2dim, label='y2')
            plt.plot(y3dim, label='y3')
            plt.plot(y4dim, label='y4')

            plt.draw()
            plt.pause(.01)
            pltgif.append(plt)

    return parameters, costdim

#------------------------------------------------------------
parameter,costdim = train(x_train, y_train, 300, 0.5, True)

A2, cache = forward_propagate(x_train0, parameter)

printf("样本|y1|y2|y3|y3")
printf("--|--|--|--|--")
for id,v in enumerate(A2.T[0:4]):
    printf("%s|%4.3f|%4.3f|%4.3f|%4.3f"%(str(x_train[id]), v[0], v[1], v[2], v[3]))

pltgif.save(r'd:\temp\1.gif')

printf('cost:%f'%costdim[-1])

#------------------------------------------------------------
plt.clf()
plt.plot(arange(len(costdim))*DISP_STEP, costdim)
plt.xlabel("Step")
plt.ylabel("Cost")
plt.grid(True)
plt.tight_layout()
plt.show()

#------------------------------------------------------------
#        END OF FILE : HW16BP.PY
#============================================================

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    • 
  
  • 111
    •

2.BP网络的子程序

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# BP1SIGMOID.PY                    -- by Dr. ZhuoQing 2020-11-17
#
# Note:
#============================================================

from headm import *

#------------------------------------------------------------
# Samples data construction

random.seed(int(time.time()))

#------------------------------------------------------------
def shuffledata(X, Y):
    id = list(range(X.shape[0]))
    random.shuffle(id)
    return X[id], (Y.T[id]).T

#------------------------------------------------------------
# Define and initialization NN
def initialize_parameters(n_x, n_h, n_y):
    W1 = random.randn(n_h, n_x) * 0.5          # dot(W1,X.T)
    W2 = random.randn(n_y, n_h) * 0.5          # dot(W2,Z1)
    b1 = zeros((n_h, 1))                       # Column vector
    b2 = zeros((n_y, 1))                       # Column vector

    parameters = {'W1':W1,
                  'b1':b1,
                  'W2':W2,
                  'b2':b2}

    return parameters

#------------------------------------------------------------
# Forward propagattion
# X:row->sample;
# Z2:col->sample
def forward_propagate(X, parameters):
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    Z1 = dot(W1, X.T) + b1                    # X:row-->sample; Z1:col-->sample
    A1 = 1/(1+exp(-Z1))

    Z2 = dot(W2, A1) + b2                     # Z2:col-->sample
    A2 = Z2                                   # Linear output

    cache = {'Z1':Z1,
             'A1':A1,
             'Z2':Z2,
             'A2':A2}
    return Z2, cache

#------------------------------------------------------------
# Calculate the cost
# A2,Y: col->sample
def calculate_cost(A2, Y, parameters):
    err = [x1-x2 for x1,x2 in zip(A2.T, Y.T)]
    cost = [dot(e,e) for e in err]
    return mean(cost)

#------------------------------------------------------------
# Backward propagattion
def backward_propagate(parameters, cache, X, Y):
    m = X.shape[0]                  # Number of the samples

    W1 = parameters['W1']
    W2 = parameters['W2']
    A1 = cache['A1']
    A2 = cache['A2']

    dZ2 = (A2 - Y)
    dW2 = dot(dZ2, A1.T) / m
    db2 = sum(dZ2, axis=1, keepdims=True) / m

    dZ1 = dot(W2.T, dZ2) * (A1 * (1-A1))
    dW1 = dot(dZ1, X) / m
    db1 = sum(dZ1, axis=1, keepdims=True) / m

    grads = {'dW1':dW1,
             'db1':db1,
             'dW2':dW2,
             'db2':db2}

    return grads

#------------------------------------------------------------
# Update the parameters
def update_parameters(parameters, grads, learning_rate):
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    dW1 = grads['dW1']
    db1 = grads['db1']
    dW2 = grads['dW2']
    db2 = grads['db2']

    W1 = W1 - learning_rate * dW1
    W2 = W2 - learning_rate * dW2
    b1 = b1 - learning_rate * db1
    b2 = b2 - learning_rate * db2

    parameters = {'W1':W1,
                  'b1':b1,
                  'W2':W2,
                  'b2':b2}

    return parameters

#------------------------------------------------------------
#        END OF FILE : BP1SIGMOID.PY
#============================================================

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    • 
  
  • 111
    • 
  
  • 112
    • 
  
  • 113
    • 
  
  • 114
    • 
  
  • 115
    • 
  
  • 116
    • 
  
  • 117
    • 
  
  • 118
    • 
  
  • 119
    •

文章来源: zhuoqing.blog.csdn.net，作者：卓晴，版权归原作者所有，如需转载，请联系作者。

原文链接：zhuoqing.blog.csdn.net/article/details/109828542

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
神经网络
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入