Matplotlib绘制简单函数的梯度下降法

举报
tsinghuazhuoqing 发表于 2021/12/27 00:58:53 2021/12/27
【摘要】   ➤01 一维函数 使用matplotlib的绘制函数是非常方便和容易的。 下面这个有趣的例子来自于飞浆PaddlePaddle深度学习实战P20中的例子。 1.简单的例子 演示了...

 

➤01 一维函数

使用matplotlib的绘制函数是非常方便和容易的。
下面这个有趣的例子来自于飞浆PaddlePaddle深度学习实战P20中的例子。

1.简单的例子

演示了对于 y = x 2 y = x^2 y=x2函数通过局部的梯度下降方法来逐步获得全局极小值。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# DEMO1.PY                     -- by Dr. ZhuoQing 2020-11-16
#
# Note:
#============================================================

from headm import *

#------------------------------------------------------------
def func(x):
    return square(x)

def dfunc(x):
    return 2 * x                    # Derivative of x**2

#------------------------------------------------------------
def gradient_descent(x_start, func_deri, epochs, learning_rate):
    theta_x = zeros(epochs+1)
    temp_x = x_start
    theta_x[0] = temp_x

    for i in range(epochs):
        deri_x = func_deri(temp_x)
        delta = -deri_x * learning_rate
        temp_x = temp_x + delta
        theta_x[i+1] = temp_x

    return theta_x

#------------------------------------------------------------
def mat_plot():
    line_x = linspace(-5, 5, 100)
    line_y = func(line_x)

    x_start = -5
    epochs = 5
    lr = 0.3
    x = gradient_descent(x_start, dfunc, epochs, lr)

    color = 'r'
    plt.plot(line_x, line_y, c='b')
    plt.plot(x, func(x), c=color, linestyle='--', linewidth=1, label='lr={}'.format(lr))
    plt.scatter(x, func(x), color=color)
    plt.xlabel('x')
    plt.ylabel('x^2')
    plt.legend()
    plt.show()

mat_plot()

#------------------------------------------------------------
#        END OF FILE : DEMO1.PY
#============================================================

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    •

▲ 绘制x**2梯度下降

▲ 绘制x**2梯度下降

2.绘制不同Learning Rate的梯度下降过程

绘制不同Learning Rate下的梯度下降方法对应的迭代过程。
▲ 学习速率从0.01增加到1.5

▲ 学习速率从0.01增加到1.5 


def mat_plot(learning_rate=0.3):
    line_x = linspace(-5, 5, 100)
    line_y = func(line_x)

    x_start = -5
    epochs = 10
    lr = learning_rate
    x = gradient_descent(x_start, dfunc, epochs, lr)

    color = 'r'
    plt.clf()
    plt.plot(line_x, line_y, c='b')
    plt.plot(x, func(x), c=color, linestyle='--', linewidth=1, label='lr=%4.2f'%lr)
    plt.scatter(x, func(x), color=color)
    plt.xlabel('x')
    plt.ylabel('x^2')
    plt.legend(loc='upper right')
#    plt.show()
    plt.draw()
    plt.pause(.001)

#------------------------------------------------------------
pltgif = PlotGIF()

for lr in linspace(0.01, 1.5, 100):
    mat_plot(lr)

    if lr > 0.01:
        pltgif.append(plt)

pltgif.save(r'd:\temp\1.gif')


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    •

 

➤02 二维函数

根据 Python 中的3Dplot 中给出的轮廓函数，来进行梯度下降的实验。

1.函数

Z ( x , y ) = e − ( x + 1 ) 2 − ( y + 0.5 ) 2 − e − ( x − 1 ) 2 − ( y − 0.5 ) 2 Z\left( {x,y} \right) = e^{ - \left( {x + 1} \right)^2 - \left( {y + 0.5} \right)^2 } - e^{ - \left( {x - 1} \right)^2 - \left( {y - 0.5} \right)^2 } Z(x,y)=e−(x+1)2−(y+0.5)2−e−(x−1)2−(y−0.5)2

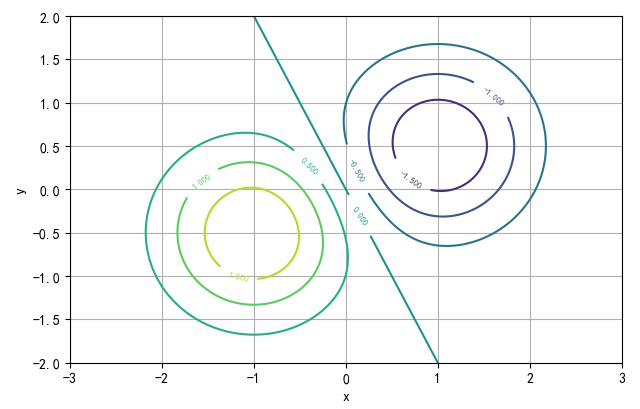
▲ 二维函数的等高线图

▲ 二维函数的等高线图 

def func(x,y):
    res = exp(-(x+1)**2-(y+0.5)**2)-exp(-(x-1)**2-(y-0.5)**2)
    return res*2

def dfunc(x,y):
    dx = -2*(x+1)*exp(-(x+1)**2-(y+0.5)**2) + 2*(x-1)*exp(-(x-1)**2-(y-0.5)**2)
    dy = -2*(y+0.5)*exp(-(x+1)**2-(y+0.5)**2) + 2*(y-0.5)*exp(-(x-1)**2-(y-0.5)**2)
    return dx*2,dy*2

def gradient_descent(x_start, y_start, epochs, learning_rate):
    theta_x = []
    theta_y = []
    temp_x = x_start
    temp_y = y_start

    theta_x.append(temp_x)
    theta_y.append(temp_y)

    for i in range(epochs):
        dx,dy = dfunc(temp_x, temp_y)
        temp_x = temp_x - dx*learning_rate
        temp_y = temp_y - dy*learning_rate

        theta_x.append(temp_x)
        theta_y.append(temp_y)

    return theta_x, theta_y

#------------------------------------------------------------
def mat_plot(learning_rate=0.3):
    delta = 0.025
    x = arange(-3.0, 3.0, delta)
    y = arange(-3.0, 3.0, delta)
    X,Y = meshgrid(x,y)
    Z = func(X, Y)

    CS = plt.contour(X, Y, Z)
    plt.clabel(CS, inline=0.5, fontsize=6)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.grid(True)
    plt.axis([-3, 3, -2, 2])
    plt.tight_layout()
    plt.show()


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    •

函数Z(x,y)对x,y求偏导数：

∂ Z ∂ x = ( − 2 x − 2 ) e − ( x + 1 ) 2 − ( y + 0.5 ) 2 − ( − 2 x + 2 ) e − ( x − 1 ) 2 − ( y − 0.5 ) 2 {{\partial Z} \over {\partial x}} = \left( { - 2x - 2} \right)e^{ - \left( {x + 1} \right)^2 - \left( {y + 0.5} \right)^2 } - \left( { - 2x + 2} \right)e^{ - \left( {x - 1} \right)^2 - \left( {y - 0.5} \right)^2 } ∂x∂Z​=(−2x−2)e−(x+1)2−(y+0.5)2−(−2x+2)e−(x−1)2−(y−0.5)2

∂ Z ∂ y = ( − 2 y − 1.0 ) e − ( x + 1 ) 2 − ( y + 0.5 ) 2 − ( − 2 y + 1.0 ) e − ( x − 1 ) 2 − ( y − 0.5 ) 2 {{\partial Z} \over {\partial y}} = \left( { - 2y - 1.0} \right)e^{ - \left( {x + 1} \right)^2 - \left( {y + 0.5} \right)^2 } - \left( { - 2y + 1.0} \right)e^{ - \left( {x - 1} \right)^2 - \left( {y - 0.5} \right)^2 } ∂y∂Z​=(−2y−1.0)e−(x+1)2−(y+0.5)2−(−2y+1.0)e−(x−1)2−(y−0.5)2

from sympy                  import symbols,simplify,expand,print_latex
from sympy                  import diff,exp

#------------------------------------------------------------
x,y,f = symbols('x,y,f')

f=exp(-(x+1)**2-(y+0.5)**2)-exp(-(x-1)**2-(y-0.5)**2)

dfdx = diff(f,x)
dfdy = diff(f,y)

result = dfdy

#------------------------------------------------------------
print_latex(result)
tspexecutepythoncmd("msg2latex")
clipboard.copy(str(result))

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    •

2.二维梯度下降

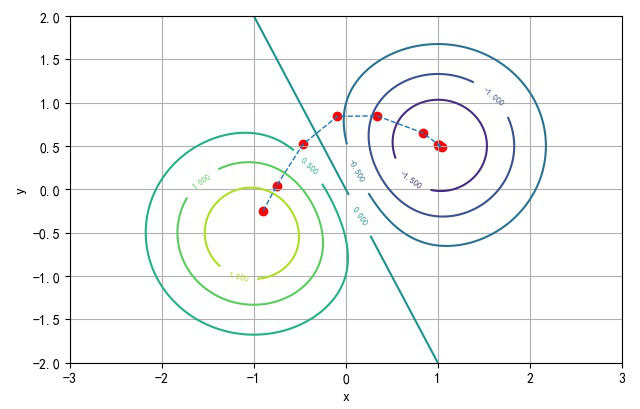
▲ 梯度下降的迭代路线

▲ 梯度下降的迭代路线

如下是在Learning-Rate=0.1， Epochs在1 ~ 21的变化的动图。

如下是：Epochs=20，Learning-Rate从0.01到1.2之间变化。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST3.PY                     -- by Dr. ZhuoQing 2020-11-16
#
# Note:
#============================================================

from headm import *

def func(x,y):
    res = exp(-(x+1)**2-(y+0.5)**2)-exp(-(x-1)**2-(y-0.5)**2)
    return res*2

def dfunc(x,y):
    dx = -2*(x+1)*exp(-(x+1)**2-(y+0.5)**2) + 2*(x-1)*exp(-(x-1)**2-(y-0.5)**2)
    dy = -2*(y+0.5)*exp(-(x+1)**2-(y+0.5)**2) + 2*(y-0.5)*exp(-(x-1)**2-(y-0.5)**2)
    return dx*2,dy*2

def gradient_descent(x_start, y_start, epochs, learning_rate):
    theta_x = []
    theta_y = []
    temp_x = x_start
    temp_y = y_start

    theta_x.append(temp_x)
    theta_y.append(temp_y)

    for i in range(epochs):
        dx,dy = dfunc(temp_x, temp_y)
        temp_x = temp_x - dx*learning_rate
        temp_y = temp_y - dy*learning_rate

        theta_x.append(temp_x)
        theta_y.append(temp_y)

    return theta_x, theta_y

#------------------------------------------------------------
def mat_plot(epochs=10, learning_rate=0.3):
    lr = learning_rate
    delta = 0.025
    x = arange(-3.0, 3.0, delta)
    y = arange(-3.0, 3.0, delta)
    X,Y = meshgrid(x,y)
    Z = func(X, Y)

    dx,dy = gradient_descent(-0.9, -0.25, epochs, lr)

    plt.clf()
    plt.scatter(dx, dy, color='r')
    plt.plot(dx, dy, linewidth=1, linestyle='--', label='lr=%4.2f'%lr)

    CS = plt.contour(X, Y, Z)
    plt.clabel(CS, inline=0.5, fontsize=6)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.grid(True)
    plt.axis([-3, 3, -2, 2])
    plt.tight_layout()
    plt.legend(loc='upper right')
    plt.draw()
    plt.pause(.001)

#------------------------------------------------------------

pltgif = PlotGIF()

for i in linspace(0.01, 1.2, 50):
    mat_plot(10, i)
    if i > 0.01:
        pltgif.append(plt)

pltgif.save(r'd:\temp\1.gif')

#------------------------------------------------------------
#        END OF FILE : TEST3.PY
#============================================================

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
 


#------------------------------------------------------------
def mat_plot(epochs=10, learning_rate=0.3):
    lr = learning_rate
    delta = 0.025
    x = arange(-3.0, 3.0, delta)
    y = arange(-3.0, 3.0, delta)
    X,Y = meshgrid(x,y)
    Z = func(X, Y)

    dx,dy = gradient_descent(-0.9, -0.25, epochs, lr)

    plt.clf()
    ax = plt.axes(projection='3d')
#    ax.plot_surface(X,Y,Z, cmap='coolwarm')
    ax.contour(X,Y,Z)

    ax.scatter(dx, dy, func(array(dx),array(dy)), color='r')
    ax.plot(dx, dy, func(array(dx), array(dy)), linewidth=1, linestyle='--', label='lr=%4.2f'%lr)

#    CS = plt.contour(X, Y, Z)
#    plt.clabel(CS, inline=0.5, fontsize=6)

    plt.xlabel('x')
    plt.ylabel('y')
    plt.grid(True)
    plt.axis([-3, 3, -2, 2])
    plt.tight_layout()
    plt.legend(loc='upper right')
    plt.draw()
    plt.pause(.1)

#------------------------------------------------------------

pltgif = PlotGIF()

for i in linspace(0.01, 1.2, 100):
    mat_plot(20, i)
    if i > 0.01:
        pltgif.append(plt)

pltgif.save(r'd:\temp\1.gif')

#------------------------------------------------------------
#        END OF FILE : TEST3.PY
#============================================================

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    •

文章来源: zhuoqing.blog.csdn.net，作者：卓晴，版权归原作者所有，如需转载，请联系作者。

原文链接：zhuoqing.blog.csdn.net/article/details/109732365

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
机器学习
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入