利用二极管的P-N结的I-V特性测量Boltzmann常数

■ 前言
在网文 An Electronic Mesurement of the Boltzmann’s Constant Using I-V Characterisctic of a Silicon 2N2309 Diode 中介绍了使用三极管2N3094来测量 Boltzmann Constant 的方法。
由于这个方法简便易行,所使用的设备也是大多数电子实验室都具备,所以称为很多电子类课程中,学生喜欢做的电子实验。
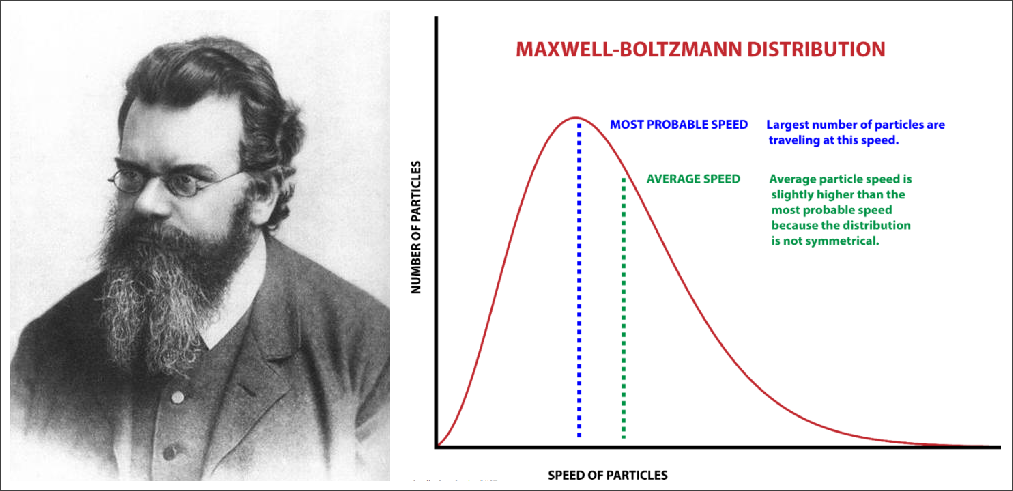
▲ Ludwig Boltzmann(1844-1904) 以及Maxwell-Boltzmann 分布
玻尔兹曼常数(Boltzmann constant),通常使用 k , k B k,kB k,kB表示,是指有关于温度及能量的一个物理常数。玻尔兹曼是一位奥地利物理学家,在统计力学的理论有重大贡献,玻尔兹曼常数具有相当重要的地位。

01实验及数据分析
1.基于2N3904的Boltzmann常数
在PN结两边,存在一个由电子-空穴扩散而形成的耗散区,以及伴随着的接触电位 V 0 V_0 V0区,只有热量动能超过 V 0 V_0 V0的电子才能够从n型区域穿越到p型区域。根据统计力学原理,处在热平衡下电子的动能分布遵循 玻尔兹曼分布 。具有能量为 e V 0 eV_0 eV0的概率为:
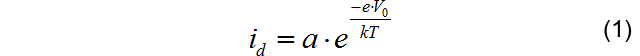
其中 i d i_d id是漂移电流, a a a是比例常数, T T T是温度, k k k是玻尔兹曼常数。
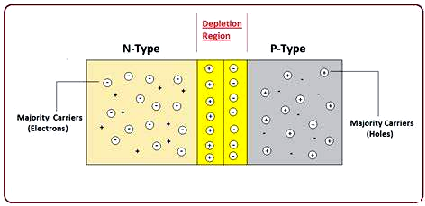
▲ PN结的结构示意图
这股漂移电流在耗散区建立一个电场 E d E_d Ed。到外部电压 V V V施加在PN结,产生电场 E D E_D ED,产生电流:
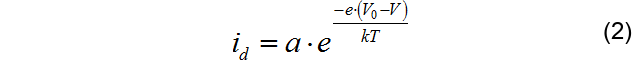
这样,外部总电流为:
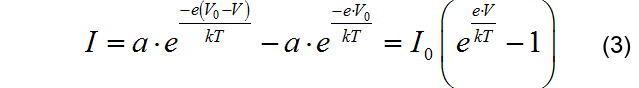
在推文开始提到的文章中,使用 2N3904 测试二极管的I-V特性。对于2N23904的电流放大和转换,选择了 LF356 运放进行I-V转换。 LF356的偏置电压为10mA和偏置电流为30pA。
下面是实验所使用的电路图。根据Measurement of Boltzmann’s constant 文献中描述,测量A,B两点的电压,便可以建立起 Q 1 Q_1 Q1的发射结对应的电压与电流之间的关系。
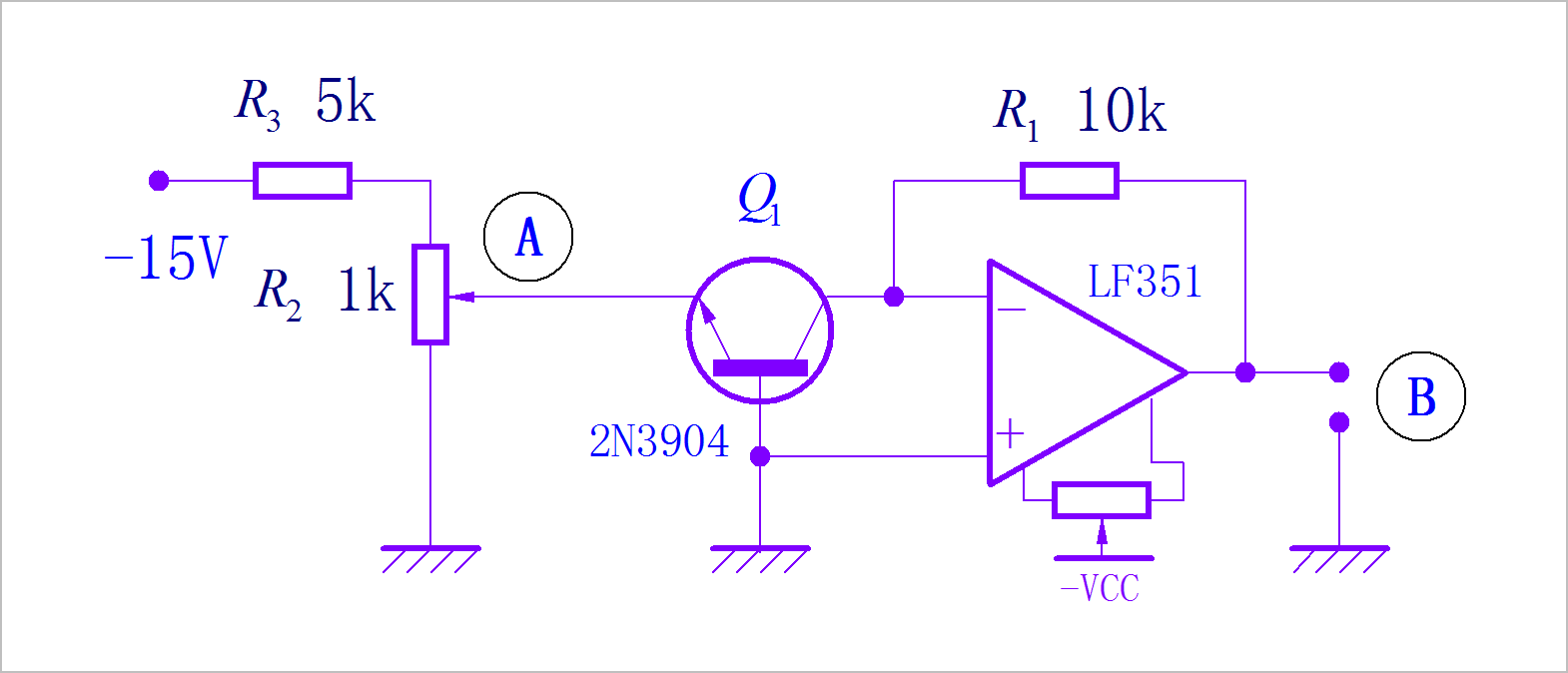
▲ 基于2N3904的PN结测量Boltzmann常数
后级的 LF351 组成电流-电压转换电路,根据电路中的参数,B点的电压与流经 Q 1 Q_1 Q1集电极电流之间的关系为: U B = I Q 1 C × 1 0 4 U_B = I_{Q1C} \times 10^4 UB=IQ1C×104。
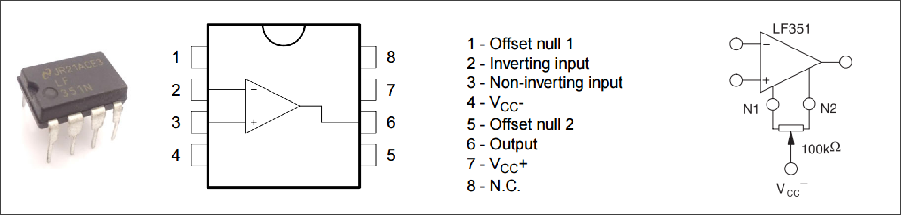
▲ JFET输入的OPAMP-LF351运放
在实验中,使用DP1308可编程直流电源的-25V输出电压串联一个10kΩ电阻做为A点给定电源。使用FLUKE45测量A点电位,使用DM3068 6 1 2 6{1 \over 2} 621 位数字万用表测量B点的电压并自动记录。
2. 测量数据分析
设置数字直流电源DP1308输出电压从**-0.2到-10V**,同时测量A,B两点的电压变化,并换算成PN结的电压-电流关系,绘制如下。
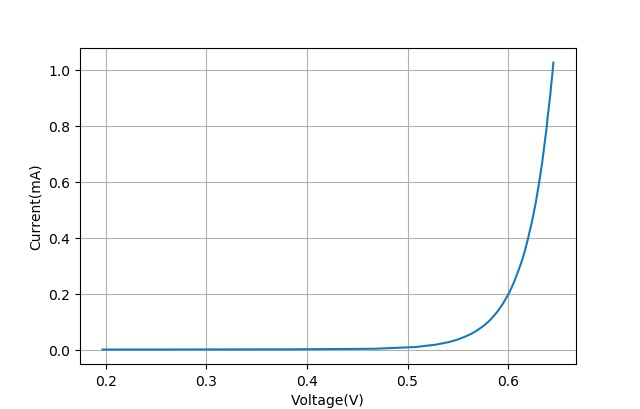
▲ 测量输入电压与电流曲线
vv=[0.19666,0.29133,0.38548,0.46684,0.50835,0.52833,0.54163,0.55082,0.55782,0.56394,0.56880,0.57302,0.57684,0.58020,0.58313,0.58579,0.58826,0.59053,0.59258,0.59455,0.59635,0.59811,0.59976,0.60135,0.60275,0.60409,0.60543,0.60665,0.60770,0.60898,0.61006,0.61118,0.61223,0.61328,0.61428,0.61518,0.61598,0.61692,0.61765,0.61840,0.61921,0.61997,0.62064,0.62134,0.62205,0.62278,0.62345,0.62408,0.62466,0.62535,0.62587,0.62648,0.62706,0.62764,0.62818,0.62867,0.62918,0.62968,0.63024,0.63069,0.63112,0.63165,0.63213,0.63249,0.63295,0.63346,0.63395,0.63427,0.63469,0.63506,0.63545,0.63586,0.63621,0.63659,0.63696,0.63735,0.63777,0.63817,0.63844,0.63878,0.63909,0.63933,0.63971,0.64012,0.64046,0.64071,0.64112,0.64151,0.64182,0.64218,0.64246,0.64269,0.64300,0.64331,0.64365,0.64398,0.64429,0.64452,0.64475,0.64512]
cc=[0.00028,0.00066,0.00111,0.00309,0.00934,0.01789,0.02737,0.03718,0.04723,0.05752,0.06778,0.07812,0.08864,0.09908,0.10968,0.12018,0.13074,0.14143,0.15200,0.16262,0.17335,0.18394,0.19461,0.20535,0.21598,0.22666,0.23746,0.24814,0.25882,0.26961,0.28032,0.29097,0.30182,0.31250,0.32317,0.33402,0.34473,0.35559,0.36628,0.37702,0.38788,0.39856,0.40931,0.42017,0.43090,0.44163,0.45252,0.46324,0.47399,0.48485,0.49542,0.50630,0.51708,0.52794,0.53868,0.54945,0.56033,0.57108,0.58183,0.59272,0.60346,0.61422,0.62511,0.63587,0.64665,0.65752,0.66831,0.67906,0.68997,0.70074,0.71148,0.72239,0.73315,0.74391,0.75482,0.76557,0.77648,0.78723,0.79801,0.80891,0.81966,0.83042,0.84134,0.85209,0.86286,0.87379,0.88452,0.89531,0.90623,0.91701,0.92777,0.93868,0.94950,0.96025,0.97118,0.98193,0.99271,1.00364,1.01442,1.02530]
- 1
- 2
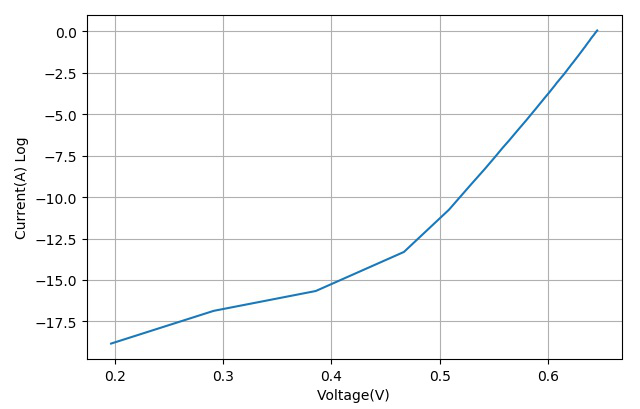
▲ 电流使用LOG尺度绘制的数据曲线
利用模型(3)匹配上述测量数据,将模式简化成下带有参数[a,b,c]的指数函数关系,利用前面测量的PN结I-V数据,使用SCIPY.OPTIMIZE中的curve_fit函数进行函数拟合,获得参数[a,b,c]的数值。
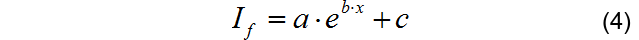
from scipy.optimize import curve_fit
vv, cc = tspload('iv2n3904', 'vv', 'cc')
def func(x, a, b, c):
return a * exp(x * b) + c
param = [0.001, 0.02, 0.0]
param, conv = curve_fit(func, vv, cc, p0=param)
printf(param)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
测量参数为:
a=2.33332986e-11
b=3.79731168e+01
c=8.85188988e-03
由模式(3)可以知道,参数b与Boltzmann常数之间的关系:
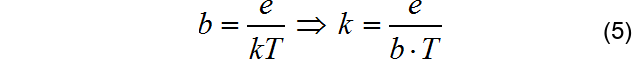
将常数e, T = 300(27摄氏度)代入上面公式,可以得到:
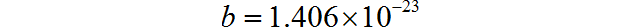
这个数值比现在测到得到精确的Botlzmann常数大了1.9%左右。在上述时间条件下,这个数值非常精确了。
3. 基于NPN 8050测试Boltzmann常数
将前面所使用的三极管2N3904更换成另外一款NPN性的硅三极管8050,使用相同的测试方案完成8050的b-e结的电压-电流测试,所得到的数据曲线如下:
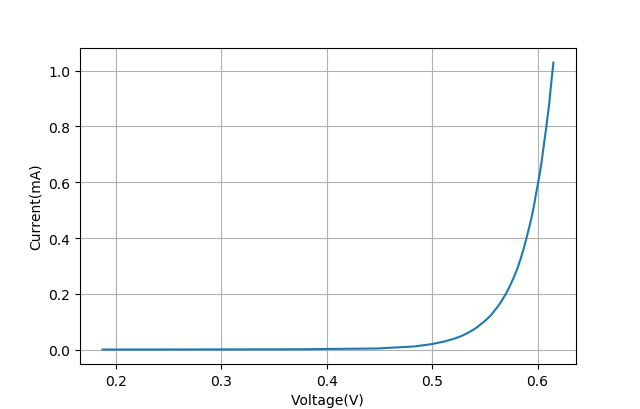
▲ 测试NPN8050的发射极PN结的I-V曲线
使用相同的方法进行建模,并计算参数:
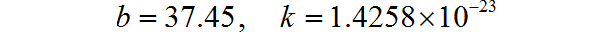
这个数值比精确Boltzmann常数大了3.29%。
4. 将2N3904的C.E对换测量
测量三级管b-c之间的PN结的电压与电流曲线。在上述实验中将2N3904的c,e管教互换,测量得到的PN结电流-电压曲线如下:
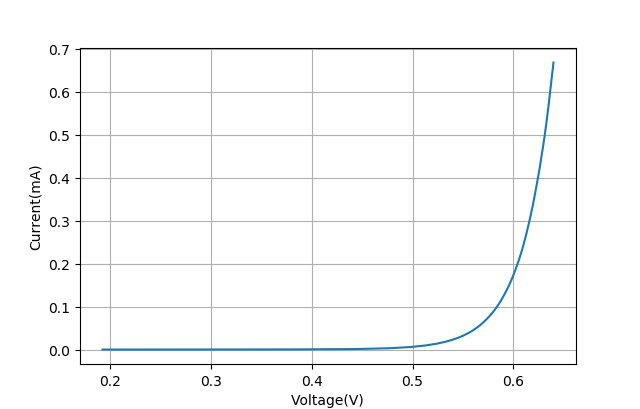
▲ 2N3904的BC的PN结的电压与电流关系
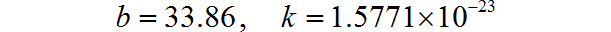
这个结果比精确Boltzmann常数大了14.2%。
5. 只使用2N3904的BE进行测量

▲ 直接对2N3904 b-e PN结测量对应的电压与电流之间的关系曲线
根据测量的电压电流曲线,可以得到对应的模型参数和Boltzmann常数如下:
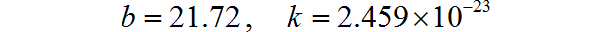
这个数值比起精确的Boltzmann常数的数值高了78.1%。
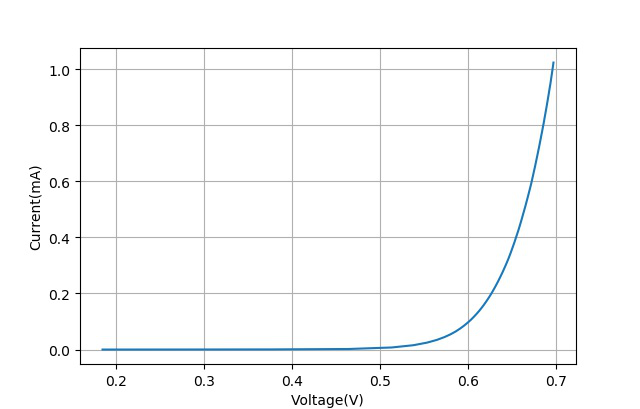
▲ 2N3904的B-E结的I-V曲线
02二极管的分段特性对结果的影响
在博文 二极管极低电流I-V特性测量 中,给出了二极管PN结的分段指数特性,即模型(3)中的电流 I 0 I_0 I0在不同的前向电流的情况下取值是不同相同,这个变化也会导致测量的Boltzmann常数发生变化。
在实验[02-1]中,选择不同测量数据的来拟合估算Boltzmann常数会产生一定的变化。下面选择2N3904测量数据中,从数据编号n=10(对应电流:0.06mA)开始,结束数据编号n从50变化到100,使用模型(3)计算相应的Boltzmann常数,对应的误差曲线如下:
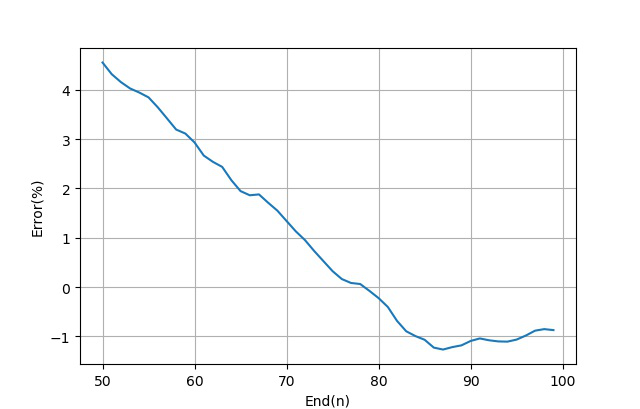
▲ 不同的二极管电流计算Boltzmann常数误差变化
从数值计算结果来看,使用前面数据测量范围(10~78),对应电流(0.06mA变化到0.7mA)时,测到得到的Boltzmann的误差最小。
※ 结论
1.PN测量不同方案比较
使用相同的PN结的模型,对于四种不同的方案测量了Boltzmann常数,其中包括有两种不同型号硅NPN双极性三极管,三极管的b-e,b-c结的测量,以及直接测量b-e的PN结电压电流的情况。
| 序号 | 方法描述 | Boltzmann常数 | 误差(%) |
|---|---|---|---|
| 1 | 2N3904的b-e的PN结 | 1.406e-23 | 1.87% |
| 2 | 8050的b-e的PN结 | 1.426e-23 | 3.29% |
| 3 | 2N3904的b-c的PN结 | 1.577e-23 | 14.24% |
| 4 | 2N3904的b-e的PN结 直接测量 | 2.459e-23 | 78.09% |
通过前面的实验,可以看到使用2N3904基极接地的配置,测量的结果误差最小。更换NPN晶体管为8050,测量的结果偏大一些。
如果将2N3904的C,E极进行对换,虽然从晶体管的结构上是对称的,但是结果误差更大。
由于PN结电压-电流模型中的参数随着电流不同,导数PN结附近半导体内部的电子与空闲运动模式变化,从而使得模型参数也发生变化。所以使用不同电流范围数据,测量数的Boltzmann的数据有所变化
2.参考文献
- Measurement of Boltzmann’s constant . Phys. Educ. 20 1996. Printed in Great Britain.

▲ 测试电路方案
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# MEAS1.PY -- by Dr. ZhuoQing 2020-07-04
#
# Note:
#============================================================
from headm import *
from tsmodule.tsvisa import *
from tsmodule.tsstm32 import *
dp1308open()
dm3068open()
setv = linspace(0.2, 10, 100)
vdim = []
idim = []
dp1308n25v(0)
time.sleep(2)
for v in setv:
dp1308n25v(v)
time.sleep(2)
meter = meterval()
iv = dm3068vdc()
ic = iv / 10
vdim.append(meter[0])
idim.append(ic)
printff(v, ic, meter[0])
dp1308n25v(0)
tspsave('iv2N3904-1', vv=vdim, cc=idim)
plt.plot(vdim, idim)
plt.xlabel("Voltage(V)")
plt.ylabel("Current(mA)")
plt.grid(True)
plt.show()
#------------------------------------------------------------
# END OF FILE : MEAS1.PY
#============================================================
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# CAL1.PY -- by Dr. ZhuoQing 2020-07-04
#
# Note:
#============================================================
from headm import *
from scipy.optimize import curve_fit
vv, cc = tspload('iv2n3904-1', 'vv', 'cc')
#vv, cc = tspload('iv8050-2', 'vv', 'cc')
e = 1.602e-19
T = 273 + 27
#------------------------------------------------------------
def func(x, a, b, c):
return a * exp(x * b) + c
#------------------------------------------------------------
param = [0.001, 0.02, 0.0]
param, conv = curve_fit(func, vv, cc, p0=param)
printf(param)
b = param[1]
printf(e/(b*T))
ccal = func(vv, *param)
plt.plot(vv, cc, label='Measure')
plt.plot(vv, ccal, label='Modal')
plt.xlabel("Voltage(V)")
plt.ylabel("Current(mA)")
plt.grid(True)
plt.legend(loc="upper right")
plt.show()
#------------------------------------------------------------
# END OF FILE : CAL1.PY
#============================================================
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
文章来源: zhuoqing.blog.csdn.net,作者:卓晴,版权归原作者所有,如需转载,请联系作者。
原文链接:zhuoqing.blog.csdn.net/article/details/107117476
- 点赞
- 收藏
- 关注作者


评论(0)